Привет, Codeforces!

Я не уверен, что эта тема не освещалась ранее, но поиск по блогам результатов не дал.

Сразу к делу

Взглянем на статью о дереве Фенвика в википедии: "Дерево Фенвика (двоичное индексированное дерево, англ. Fenwick tree, binary indexed tree, BIT)..."

Разве дерево Фенвика является двоичным? В общем случае — нет. На рисунке ниже дерево Фенвика изображено в виде... дерева! Дело в том, что в подавляющем большинстве материалов, авторы не пытаются указать, почему дерево Фенвика — дерево.

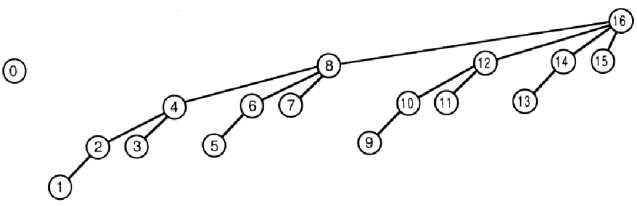
Почему недвоичное дерево назвали двоичным?

Все дело в неверном переводе составного прилагательного "Binary Indexed", одним из корректных переводов которого является "двоично-индексируемое". В ошибочном варианте перевода "Binary" и "Indexed" воспринимаются, как два самостоятельных прилагательных — "двоичное" и "индексированное".

А что такое двоично-индексируемое дерево?

Дерево, вершины которого пронумерованы числами так, что номера (индексы) вершин-сыновей вычисляются с помощью битовых операций над номером вершины-родителя. Помимо дерева Фенвика, яркими примерами двоично-индексированных деревьев служат двоичная куча (в классической реализации) и дерево отрезков, написанное на массиве. Кстати, эти примеры — не самые удачные, т.к. в них фигурируют двоичные двоично-индексирумые деревья, поэтому рассмотрим еще один пример. Имеется полное дерево степени 4, корень которого имеет индекс 0, а сыновья вершины x имеют индексы (x <  < 2) + 1, (x <  < 2) + 2, (x <  < 2) + 3, (x <  < 2) + 4, где  <  <  — двоичный сдвиг влево.

Надеюсь, этот пост будет полезен тем, кто еще не разобрался с деревом Фенвика. Спасибо за внимание!