Прошу прощения за задержку с разбором.
731A - Ночь в музее
Автор задачи: egor-belikov, разработчик: timgaripov
В этой задаче требуется реализовать то, что написано в условии, т. е. явно посчитать минимальное количество поворотов, которое нужно совершить от буквы a до первой буквы слова, от первой буквы слова до второй, и так далее. Единственное полезное знание, которое может чуть-чуть упростить жизнь, это то, что расстояние между точками x и y на окружности длины l (26 в нашем случае) можно посчитать как min(|x - y|, l - |x - y|).
Данное решение работает за O(|s|), и, конечно же, укладывается в любые ограничения.
731B - Купоны и скидки
Автор задачи: жюри олимпиады, разработчик: platypus179
Заметим, что в корректном ответе можно гарантировать, что для любых двух последовательных дней мы пользуемся не более одним купоном, покупая две пиццы именно в эти дни. Действительно, если у нас есть два купона на покупку пицц в дни i и i + 1, давайте заменим эти два купона на две скидки в дни i и i + 1.
Посмотрим на первый день. Согласно утверждению выше, мы можем однозначно определить, сколько купонов на покупку пицц в 1 и 2 дни мы используем: либо 0, если в первый день было куплено чётное число пицц, либо 1, в противном случае. Оставшиеся пиццы в этот день можно покупать по скидкам. Если мы действительно пользуемся купоном, вычтем из количества пицц во второй день единицу, и перейдём ко второму дню, повторяя те же самые действия.
Может так случиться, что в очередной день у нас и количество пицц нечётное, и в следующий день не надо купить ни одной пиццы. Это значит, что добиться требуемого одними купонами и скидками невозможно, и можно выводить "NO". Если же такого не случилось, то мы справились всё купить, используя только купоны и скидки.
Чуть-чуть подумав, можно понять, что описанное решение доказываетт, что ответ — "YES" тогда и только тогда, когда на любом максимальном отрезке из подряд идущих ненулевых чисел сумма чисел чётная.
Данное решение работает за O(n).
731C - Носки
Автор задачи: egor-belikov, разработчик: wilwell
При решении этой задачи удобно перейти к графовой интерпретации. Рассмотрим граф, в котором носками соответствуют вершины, а рёбрами соединены те носки, которые оказываются вдвоём на ногах у Арсения в какой-то день. По условию мы должны гарантировать, что любые две вершины, соединённые ребром, имеют одинаковый цвет. Это значит, что любая компонента связности в данном графе должна в итоге состоять из вершин одного цвета.
Будем для каждой компоненты связности определять, в какой цвет её надо перекрасить. Чтобы перекрасить как можно меньшее количество вершин, надо как можно большее количество вершин оставить с оргинальным цветом, значит, надо выбрать тот цвет, который в компоненте связности имеют как можно больше вершин.
Таким образом, решение принимает следующий вид: выделяем компоненты связности, в каждой компоненте связности определяем цвет, который встречается больше всего раз (например, выписав все цвета в список и отсортировав), и прибавляем к ответу разность размера компоненты связности и количества вершин этого цвета.
Данное решение работает за 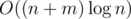 .
.
Дополнительный вопрос: Как написать решение, чтобы оно работало за O(n + m)?
731D - Археология 80-го уровня
Автор задачи: жюри олимпиады, разработчик: Flyrise
Обозначим за x количество циклических сдвигов алфавита, которые мы произведём. Наша цель — оформить в виде каких-то соотношений на x условие о лексикографической упорядоченности набора слов.
Заметим, что x действительно можно считать числом от 0 до c - 1, т. е., остатком по модулю c. Будем также считать, что все символы тоже имеют значения от 0 до c - 1, для этого вычтем из каждого символа 1.
Рассмотрим какие-нибудь два последовательных слова в списке. Возможно два варианта, соответствующих двум случаям в определении лексикографического сравнения:
Во-первых, может существовать такая позиция, что эти слова отличаются в этой позиции, а до этой позиции совпадают. Пусть, скажем, в этой позиции у первого слова стоит значение a, а у второго -- значение b. Тогда эти слова будут идти в лексикографическом порядке тогда и только тогда, когда 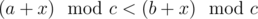 . Нетрудно видеть, что если представить все остатки по модулю c в виде окружности, то это условие задаёт дугу на этой окружности. Таким образом, эта пара последовательных слов даст нам условие вида "x принадлежит к некоторой дуге на окружности".
. Нетрудно видеть, что если представить все остатки по модулю c в виде окружности, то это условие задаёт дугу на этой окружности. Таким образом, эта пара последовательных слов даст нам условие вида "x принадлежит к некоторой дуге на окружности".
Во-вторых, такой позиции может не существовать, т. е. одно слово может быть префиксом другого. Если первое слово префикс второго, то эти два слова всегда идут в лескикографическом порядке, вне зависимости от выбора x. В противном случае (второе слово является собственным префиксом первого), мы ничего не можем поделать с этими двумя словами, и они никогда не будут идти в лексикографическом порядке, т. е. можно сразу выводить ответ - 1.
Теперь нам требуется определить, есть ли какая-то точка, лежит на всех дугах из заданного набора, или нет. Пусть у нас образовалось k условий, задающих дугу. Разорвём окружность, представив её в виде отрезка от 0 до c - 1. Каждая дуга превратится либо в один, либо в два подотрезка этого отрезка (в зависимости от того, содержала ли дуга числа 0 и c - 1 или нет).
Теперь мы должны проверить, есть ли точка, накрытая ровно k отрезками. Это можно сделать разными способами, например, можно прибавить единицу на каждом из этих отрезков с помощью какой-то структуры данных, или без её использования, поставив в начало каждого отрезка 1, а в точку после конца каждого отрезка - 1, и перейдя к префиксным суммам. А можно выписать все события открытия или закрытия какого-то отрезка, отсортировать по координате, и пройти слева направо, поддерживая количество открытых отрезков. Если в какой-то момент у нас имеется ровно k открытых отрезков, то ответ — "YES".
731E - Веселая игра
Автор задачи: meshanya, разработчик: ipavlov
Для начала хочется дать небольшой комментарий по данному виду игр. В большой науке игра, в которой двое игроков максимизируют разность между своими очками и очками соперника называется "игра с нулевой суммой". Стоит запомнить, что задачи на данный вид игр очень часто решаются с помощью динамического программирования общего вида, которое мы сейчас опишем в решении.
Заметим, что в любой момент игры на первом стикере будет написана сумма чисел на каком-то префиксе исходной последовательности чисел. Это значит, что состояние игрового поля описывается одним-единственным числом i: длиной префикса чисел исходной последовательности, которые были просуммированы в одно число.
Выскажем два соображения. Во-первых, для каждого состояния i ход, которым будет пользоваться игрок, оказавшийся в этом состоянии, не зависит от количества очков на счету у игрока и у его противника. Действительно, в любой момент игры можно не думать об очках, которые есть на счетах у игроков сейчас, потому что они дают какой-то константный вклад в итоговую разность очков, если мы мысленно занулим количества очков на счетах игроков на текущий момент. Таким образом, всё, что надо знать про состояние i -- это какая разность будет между очками игрока и между очками его противника, если бы игра начиналась с состояния i с нулевыми очками.
Во-вторых, игра симметричная, т. е. то, какой ход совершит игрок, оказавшийся в состоянии i, и с какой разностью очков в итоге закончится игра, не зависит от того, какой именно игрок оказался в этом состоянии.
Обозначим за D[i] разность очков между счётом первого игрока и счётом второго игрока, если бы игра начиналась из состояния i с нулевыми очками.
Удобно размышлять об этой игре, считая, что у игроков нет своих очков, но есть чиселнный баланс между ними, и первый игрок прибавляет на своём ходу какие-то числа к этому балансу, а второй вычитает. В таких терминах D[i] это изменение баланса к концу игры, если текущий игрок стремится его максимизировать, и сейчас он находится в состоянии i. Ответом на задачу будет являться, как несложно понять, число D[1]. Заметим, что если бы текущий игрок стремился минимизировать баланс, то, в силу симметричности игры, итоговое изменение баланса из состояния i бы составило - D[i].
Посчитаем все D[i] с помощью динамического программирования. В конце игры, т. е., в состоянии n значение D[n] равняется нулю, потому что игроки больше не будет совершать ходов, а значит, баланс не будет претерпевать изменений.
Пусть сейчас у нас какое-то состояние i. Переберём, сколько стикеров себе возьмёт текущий игрок. Если он возьмёт стикеры, заканчивая j-м (в исходной нумерации), то он изменит баланс на S[j] (пуолчит именно столько очков, где S[j] — сумма первых j чисел в исходной последовательности), а игра окажется в состоянии j, значит, его противник после этого добавит к балансу ещё - D[j] (обратите внимание, что знак изменения баланса меняется, потому что из нового состояния будет уже играть противник, а он меняет баланс в другую сторону).
Значит, итоговое изменение баланса при совершении описанного хода будет S[j] - D[j]. В определении динамики мы играем за игрока, стремящегося максимизировать баланс, значит, 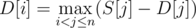 .
.
Эта формула даёт нам решение за время O(n2), но не трудно видеть, что, достаточно поддерживать максимум величины S[j] - D[j] на суффиксе j > i, пересчитывая его за O(1) при уменьшении i. Таким образом, мы получаем решение за O(n).
Дополнительный вопрос: какой тип данных надо использовать для хранения D[i] (и ответа, в частности)?
731F - Видеокарты
Автор задачи: жюри олимпиады, разработчик: vintage_Vlad_Makeev
Первым несложным соображением является то, что при фиксированной ведущей видеокарте мы можем смело брать все видеокарты такой же или большей мощности, так как каждая из них даёт строго положительный вклад в итоговую мощность. Значит, можно отсортировать карты по возрастанию мощности, и считать, что мы всегда берём какой-то суффикс видеокарт в этой последовательности.
Зафиксируем мощность ведущей видеокарты x. Суммарную мощность при таком выборе можно записать как 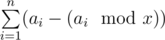 . Заметим, что под знаком суммированиия стоит число, с одной стороны, строго делящееся на x, а с другой — не превосходящее 200 000. Значит, различных значений, которые участвуют в этой сумме, не больше
. Заметим, что под знаком суммированиия стоит число, с одной стороны, строго делящееся на x, а с другой — не превосходящее 200 000. Значит, различных значений, которые участвуют в этой сумме, не больше 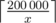 . Попытаемся посчитать значение этой суммы за сложность, пропорциональную количеству различных слагаемых в ней.
. Попытаемся посчитать значение этой суммы за сложность, пропорциональную количеству различных слагаемых в ней.
Для этого надо понять для каждого из значений x, 2x, 3x, ..., сколько видеокарт будут в итоге давать ровно такую мощность. Это несложно: в итоге мощность kx окажется ровно у всех видеокарт, которые обладают мощностью от kx до (k + 1)x - 1. Их количество можно определить за O(1), если построить массив C[i], который хранит количество видеокарт каждой мощности, и посчитать на нём все частичные суммы.
Таким образом, мы получили решение, которое делает порядка 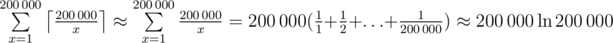 операций (про сумму в скобках полезно знать, что она называется гармоническим рядом, и что она практически не отличается от натурального логарифма количества слагаемых).
операций (про сумму в скобках полезно знать, что она называется гармоническим рядом, и что она практически не отличается от натурального логарифма количества слагаемых).
Значит, мы получили решение за сложность 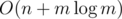 , где m -- максимальная из мощностей видеокарт.
, где m -- максимальная из мощностей видеокарт.
Дополнительный вопрос: Возникает соблазн написать неправильное решение, которое предполагает, что оптимальная мощность всегда находится среди первых, скажем, 100 мощностей в порядке сортировки. Как построить тест, в котором оптимальная мощность находится, скажем, между одной четвертью и тремя четвертями отсортированного списка мощностей, т. е. тест, который валит описанное решение?











How to solve E if it was modified by "Instead of replacing first k ≥ 2 stickers by a new stricker S' with value of their sum, we replace S' by first two stickers only."
I got stuck with problem C because I completely missed the
he has to finalize the colors now.part. I thought we could change the colors more than once.Any idea how to solve this problem in a reasonably amount of time if it's valid to change the colors more than once, i.e., every day you can choose to change the colors as needed? Not surprisingly I couldn't come up with a good idea.
По задаче С
Пожалуйста объясните, как быстро считать максимальный цвет в одной компоненте связности? Моё решение с карманом не проходит по времени (TLE тест 32) из-за необходимости обнулять карман для каждой новой компоненты, но как делать иначе я не придумал.
Можно так
Спасибо
Или за линию 21596717 (быстрее почему-то не стало :D)
Потому что bottleneck не константа в алгоритме (логарифм, по сути тут просто какая-то константа), а скорость чтения из stdin :)
21613526
Can someone give a better explanation for problem-D. I was not able to follow the editorial that well. Thanks !
Imagine that you have only 2 sequences. You'd calculate the set of non-negative integers A, that for every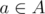 if you perform a changes, then the first sequence is lexicographically not greater than the second. Then you do this for every n - 1 pairs of sequences (the 1st and the 2nd, the 2nd and the 3rd, the 3rd and the 4th, and so on...), so you calculate A1, A2, ... An - 1 sets. The answer is in the set
if you perform a changes, then the first sequence is lexicographically not greater than the second. Then you do this for every n - 1 pairs of sequences (the 1st and the 2nd, the 2nd and the 3rd, the 3rd and the 4th, and so on...), so you calculate A1, A2, ... An - 1 sets. The answer is in the set 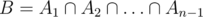 , if it's empty then answer is - 1.
, if it's empty then answer is - 1.
For more information how to deal with sets, check out my submission: 21613184 (basically you make an array and use partial sums)
Any one found anything greedy for the E?
i tried either taking all the numbers on the first step or taking the first n-1 numbers , got WA
can't find a case where the difference between both answers will be larger than the difference of either all the array and 0 or forcing the enemy to take a negative value then forcing him on the last array number,
But this doesn't seem right....
4 3
0 3 -4 2
There's your counter test case. ( ̄<  ̄)>
Another (more complex) idea of problem E.
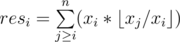
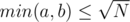
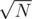 operation per one. There are two cases:
operation per one. There are two cases: 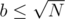 .
.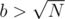 . So try
. So try 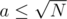
Sort all values, than calculate res[i] — answer for videocardi like leader.
N = a * b, so that
We iterate over videocards and want to do no more than
1) Current videocard is leader. We assign xi like a and try
2) Current videocard isn't leader. We assign xi like N and want to add xi to some leader videocard, where
There is basic idea. You can check my solution for more details or ask me
can anyone help me with the F I am not able to understand it
Ask a more specific question.
It seems that I solved DIV 2 C (SOCKS) problem same way as mentioned in editorial but getting TLE on test #33. Any suggestions for optimization?? or is my solution wrong?? Any help is appreciated. Thanks
My Submission
my tle submission — tle my ac submission — ac
Thanks, got it accepted by inserting colors in the set and then resetting count array to zero. But shouldn't this approach be slower than the last one? We have inserted n elements in set in O(N log N) time, whereas the previous approach took only O(n) time. Why was it getting TLE then??? Again, any help will be appreciated.
In tle solution, every time I visit a non-visited node, I am assigning tot[node] to zero for all node, which is taking O(n) time. Suppose you have to perform bfs n/2 times then, you running time complexity would be O(n^2). But after inserting values in set,I only have have to assign those values to zero which I have visited in current bfs operation .
Wow...!! Never thought of that. I always ignored initialisation during analysis. Thanks. Something good came out that TLE.
I think, best way to do this is to use map and clear the map after each dfs, it takes less memory than total memory of array and set. Correct me if I am wrong.
In E, tc 2 4 1 -7 -2 3 move 1, petya takes 1 -7 score p -6 g 0 seq -6 -2 3 move 2, gena takes -6 -2 3 score p -6 g -5 game ends diff -6 — (-5) = -1 what's wrong? -1 is better than -3