Задача A(div 2) — ЛНПП
Предполагалось, что эту задачу можно решить, не читая её условия, а только глядя на примеры :)
Найдём в заданной строке символ, который идёт в алфавите позже всех, обозначим его через z. Если этот символ встречается в строке p раз, то ответ — это строка a, состоящая из символа z, повторённого p раз.
Почему это так? Из определения лексикографического сравнения и из того, что символ z — максимальный в строке, несложно понять, что если какая-то другая подпоследовательность b заданной строки лексикографически больше a, то строка b обязана иметь большую длину, чем a, и при этом a должна являться префиксом (началом) b. Однако строка b должна также быть палиндромом, поэтому последний её символ — обязательно z. В таком случае в строке b должно быть больше вхождений символа z, чем в исходной строке s, что невозможно, так как b --- подпоследовательность s.
Кроме того, ограничение на длину строки было совсем небольшим, поэтому задачу можно было решить перебором всех подпоследовательностей строки. Для каждой из них нужно проверить, является ли она палиндромом, и из всех являющихся выбрать лексикографически наибольшую. Сложность такого решения составляет O(2n·n), где n — длина строки (в отличие от решения выше, сложность которого O(n)).
Задача В(div 2) — Инновационно новая простая задача
Ограничения в задаче были настолько малы, что проходило решение со сложностью O(m·kn). В описании каждой задачи достаточно перебрать все возможные подпоследовательности слов, являющиеся перестановками описания Лёшиной задачи, для каждой из них вычислить количество инверсий, и выбрать перестановку с минимальным количеством инверсий. Это можно сделать либо с помощью рекурсии, либо, например, с помощью необходимого количества вложенных циклов (от 1 до 4).
Вот пример псевдокода для случая n = 4:
w - массив слов задачи Лёши
s - описание очередной задачи из архива
best = 100
for a = 1 to k do
for b = 1 to k do
for c = 1 to k do
for d = 1 to k do
if s[a] == w[1] and s[b] == w[2] and s[c] == w[3] and s[d] == w[4] then
inversions = 0
if a > b then inversions = inversions + 1
if a > c then inversions = inversions + 1
if a > d then inversions = inversions + 1
if b > c then inversions = inversions + 1
if b > d then inversions = inversions + 1
if c > d then inversions = inversions + 1
if inversions < best then
best = inversions
В конце нужно выбрать задачу с минимальным значением best и вывести ответ в соответствующем формате.
Задача A(div 1)/C(div 2) — Чёткая симметрия
Интересно, что первоначально у авторов была идея не включать случай x = 3 в претесты. Представьте, сколько было бы в этом контесте сделано успешных взломов — при том, что из первых 43 решений по этой задаче ни одно претесты не прошло :)
Заметим, что ответ n — всегда нечётное число. Действительно, если n чётно, то две центральные строки матрицы A обязаны содержать только нули — в противном случае найдутся две соседние клетки, содержащие единицы. Аналогичное требование относится и к двум центральным столбцам матрицы A. Заменив две центральные строки на одну и два центральных столбца на один, при этом оставив в них нули, получим матрицу с такой же остротой, но со стороной на единицу меньше.
Заметим, что острота матрицы со стороной n не может превысить 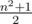 . Несложно убедиться, что на квадратное поле со стороной n можно выложить
. Несложно убедиться, что на квадратное поле со стороной n можно выложить 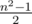 "доминошек" 1 на 2 так, чтобы "доминошки" не пересекались (иными словами, все клетки, кроме одной, можно разбить на пары так, что клетки в каждой паре имеют общую сторону). Тогда в соответствующей матрице под клетками, покрытыми одной "доминошкой", может располагаться не более одной единицы. Значит, общее количество единиц не превышает
"доминошек" 1 на 2 так, чтобы "доминошки" не пересекались (иными словами, все клетки, кроме одной, можно разбить на пары так, что клетки в каждой паре имеют общую сторону). Тогда в соответствующей матрице под клетками, покрытыми одной "доминошкой", может располагаться не более одной единицы. Значит, общее количество единиц не превышает 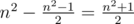 .
.
Заметим, что матрица со стороной n и остротой 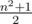 при нечётном n существует. Раскрасим все клетки матрицы в шахматном порядке и в чёрные клетки поставим единицы, а в белые — нули. Несложно убедиться, что такая матрица является и чёткой, и симметричной, и при этом имеет остроту ровно
при нечётном n существует. Раскрасим все клетки матрицы в шахматном порядке и в чёрные клетки поставим единицы, а в белые — нули. Несложно убедиться, что такая матрица является и чёткой, и симметричной, и при этом имеет остроту ровно 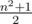 .
.
Интуитивно кажется, что раз существует матрица с остротой 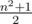 , то существует матрица и с любой меньшей остротой. Это верно всегда, кроме одного-единственного случая — не существует матрицы со стороной 3 и остротой 3, хотя и существует матрица со стороной 3 и остротой 5.
, то существует матрица и с любой меньшей остротой. Это верно всегда, кроме одного-единственного случая — не существует матрицы со стороной 3 и остротой 3, хотя и существует матрица со стороной 3 и остротой 5.
Покажем, что утверждение выше верно при нечётных n ≥ 5. Построим матрицу с остротой 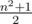 , как показано выше, и будем постепенно превращать единицы в нули, уменьшая остроту. Клетки с единицами в матрице бывают трёх типов.
, как показано выше, и будем постепенно превращать единицы в нули, уменьшая остроту. Клетки с единицами в матрице бывают трёх типов.
Первый тип — центральная клетка. Она ровно одна, при этом можно превратить число в ней в ноль, и матрица не перестанет удовлетворять условию задачи.
Второй тип — клетки в центральной строке и в центральном столбце (кроме центральной клетки). Такие клетки из условия симметричности разбиваются на пары — если мы заменяем значение в одной из них на ноль, мы обязаны также заменить на ноль значение в парной ей клетке.
Третий тип — все остальные клетки. Из условия симметричности они разбиваются на четвёрки — если мы заменяем значение в некоторой клетке третьего типа на ноль, мы должны заменить на ноль значения во всех клетках той же четвёрки.
Теперь для получения требуемой остроты x будем действовать жадно. Будем заменять единицы на нули в клетках третьего типа, делая это в четырёх клетках сразу, до тех пор, пока текущая острота превышает x как минимум на 4 и ещё есть клетки третьего типа с единицами. После этого начнём убирать клетки второго типа по парам, пока текущая острота превышает x хотя бы на 2. К этому моменту острота матрицы равна либо x, либо x + 1. Если она равна x + 1, поставим ноль в центральной клетке и получим матрицу с остротой x. Несложно проверить, что мы сможем получить матрицу любой остроты, действуя по этому жадному алгоритму.
Почему такие же рассуждения не работают при n = 3? Потому что в матрице с остротой 5, полученной из шахматной раскраски, отсутствуют клетки второго типа. При n ≥ 5 в такой матрице присутствуют клетки всех типов, что и является залогом успеха. Ответы для x ≤ 5 лучше найти вручную, но аккуратно — например, многие участники решили, что при x = 2 ответ 5, а не 3.
Задача В(div 1)/D(div 2) — Угадай автомобиль!
Нам нужно найти такие x и y, при которых величина 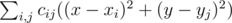 принимает минимальное возможное значение. Эту величину можно преобразовать к виду
принимает минимальное возможное значение. Эту величину можно преобразовать к виду 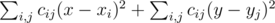 , и заметить, что поскольку левая часть не зависит от y, а правая от x, то можно минимизировать каждую из частей по отдельности. Рассмотрим, как минимизировать часть
, и заметить, что поскольку левая часть не зависит от y, а правая от x, то можно минимизировать каждую из частей по отдельности. Рассмотрим, как минимизировать часть 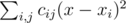 , вторая минимизируется аналогично. Поскольку выражение в скобках не зависит от j, эту часть можно переписать в виде
, вторая минимизируется аналогично. Поскольку выражение в скобках не зависит от j, эту часть можно переписать в виде 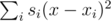 , где
, где 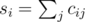 . Теперь достаточно просто перебрать все возможные значения x, и вычислить для каждого из них искомую величину, после чего выбрать x, для которого это значение минимально. Точно так же находится оптимальное значение y.
. Теперь достаточно просто перебрать все возможные значения x, и вычислить для каждого из них искомую величину, после чего выбрать x, для которого это значение минимально. Точно так же находится оптимальное значение y.
Итоговая сложность решения — O(n·m + n2 + m2).
В силу выпуклости целевой функции возможны и другие подходы к решению задачи, например, градиентый спуск либо аналитический метод (вычисление производных).
Главный действующий герой задачи — Ra16bit.
Задача С(div 1)/E(div 2) — Хрупкие мосты
Эту задачу можно решить несколькими способами, в разборе представлен один из них.
Для любого решения полезно заметить следующий факт. Допустим, искомый путь начинается на платформе i и заканчивается на платформе j (i ≤ j, если это не так, можно поменять начало и конец пути местами). Тогда все мосты, находящиеся между платформами i и j, будут пройдены в этом пути нечётное число раз, а все остальные мосты — чётное число раз.
Давайте найдём максимальную длину пути с концами на платформах i и j. Для этого для всех платформ найдём вспомогательные величины: lefti — максимальная длина пути, начинающегося и заканчивающегося на платформе i и при этом проходящего только по мостам левее платформы i; rightj — аналогично для мостов правее платформы j. Также для каждого моста определим oddi — наибольшее нечётное число, не превосходящее ai, и для каждой платформы определим sumOddi — сумму oddj по всем мостам левее платформы i.
Тогда максимальная длина пути с концами на платформах i и j (i ≤ j) равна lefti + rightj + (sumOddj - sumOddi) или, что то же самое, (rightj + sumOddj) + (lefti - sumOddi).
Теперь мы можем найти пару (i, j), для которых эта величина наибольшая, за линейное время. Переберём j. Из формулы очевидно, что нужно найти такое i ≤ j, что (lefti - sumOddi) максимально. Если перебирать j от 1 к n, то можно хранить текущее максимальное значение этой величины для всех i ≤ j и пересчитывать его при переходе к следующему j, сравнив (leftj - sumOddj) с текущим максимумом и, возможно, этот максимум обновив. Таким образом, для каждого j нужно проверять не все значения i ≤ j, а только одно.
Осталось показать, как быстро искать все lefti (все rightj ищутся аналогично). Понятно, что left1 = 0, далее будем считать lefti, используя lefti - 1. Заметим, что если ai - 1 = 1, то lefti = 0, так как после перехода по мосту на платформу (i - 1) этот мост рухнет и вернуться на платформу i уже будет невозможно. Если же ai - 1 > 1, то lefti = lefti - 1 + eveni - 1, где eveni - 1 — наибольшее чётное число, не превосходящее ai - 1. Действительно, можно перейти по мосту на платформу (i - 1), проделать путь, соответствующий lefti - 1, а потом ходить по мосту между платформами (i - 1) и i, пока лимит на количество переходов не станет меньше 2 (при этом закончить нужно на платформе i).
Таким образом, общая сложность этого решения — O(n).
Задача D(div 1) — Инновационно новая задача
Первое решение, которое приходит на ум — рекуррентное соотношение f[i][j] = (минимальное возможное количество инверсий, если среди первых j слов встречается перестановка слов, входящих в маску i). В таком решении параметр j изменяется от 0 до 500000, i — от 0 до 215 - 1, а пересчёт значений происходит за O(1) (либо используем очередное слово, либо нет). Это слишком много.
Воспользуемся стандартным приёмом: перенесём значение соотношения в параметр, а один из параметров сделаем значением. Это можно сделать не для любого рекуррентного, но для этого как раз можно :)
Понятно, что при фиксированном подмножестве слов и количестве инверсий оптимально выбрать самые ранние вхождения этих слов, которые дают такое количество инверсий. Пусть f[i][j] = (минимальное число z такое, что среди первых z слов найдётся перестановка слов из маски i, содержащая в точности j инверсий). База — f[0][0] = 0, f[0][j] = ∞ для j > 0. Пересчёт значений происходит следующим образом: перебираем слово q из маски i, которое было последним. Зная это слово, и количество инверсий j, легко вычислить количество инверсий j', которое было без этого слова — это j минус количество слов в маске, больших q (по номеру в описании Лёшиной задачи). Пусть p = f[i^(1«q)][j']. Тогда в качестве очередного возможного значения для f[i][j] нужно рассмотреть индекс p2, равный позиции следующего вхождения слова q после позиции p. Для быстрого поиска таких значений необходимо заранее для каждой задачи из архива посчитать массив next[500010][15] такой, что next[i][j] = (минимальный индекс k > i такой, что k-е слово в описании текущей задачи равно j-му слову в описании задачи Лёши). Такой массив несложно посчитать за один проход справа налево.
Суммарное количество операций можно вычислить по формуле m·(k·n + 2n·Cn2·n), где m — количество задач в архиве, k — количество слов в описании одной задачи, n — количество слов в описании задачи Лёши. При заданных ограничениях эта величина составляла около 200 миллионов, и авторские решения (включая решение на Java) работали не более двух секунд. TL был выставлен довольно-таки лояльно, 5 секунд.
Главные действующие герои задач D(div 1) и B(div 2) — Chmel_Tolstiy и ivan.metelsky.
Задача E(div 1) — Насквозь бюрократическая организация
Давайте представим, что у нас в распоряжении есть функция maxN(m, k), которая по заданным m и k возвращает максимальное значение n такое, что задачу для n людей и m пустых строчек в бланке можно решить за k запросов. Тогда можно применить бинарный поиск по ответу — количеству запросов k.
Допустим, мы сделали какие-то k запросов. Сопоставим каждому из n человек строку из k бит, где i-ый бит равен единице, если этот человек был указан в i-ом запросе, и равен нулю в противном случае. Заметим, что мы сможем определить точную дату приёма для каждого человека в том и только в том случае, если всем n людям соответствуют попарно различные k-битовые строки. На самом деле, если двум людям соответствуют одинаковые строки, то они могли бы поменяться датами между собой и ответы на запросы не изменились бы. Если же всем людям соответствуют разные строки, для каждой даты можно определить, кто именно записан на эту дату, рассмотрев множество запросов, в ответах на которые эта дата фигурирует, и найдя человека, который указан ровно в том же множестве запросов.
Ограничение в m пустых строчек в бланке означает, что в каждой из k позиций в строках суммарное число единиц по всем n числам не должно превышать m. Таким образом, функция maxN(m, k) должна возвращать максимальную мощность множества различных k-битовых строк, для которых выполняется это ограничение. Давайте ослабим это ограничение: будем искать множество, в котором в сумме по всем разрядам количество единиц не превышает k·m. Как мы докажем после, ответ от этого не изменится.
С таким ослабленным ограничением задача решается простым жадным алгоритмом. Логично, что сначала лучше брать те строки, в которых меньше единиц. Будем перебирать количество единиц i в строке от 0 до k, а также хранить переменную t, обозначающую количество единиц, которое ещё можно поставить (изначально она равна k·m). Тогда на i-ом шаге максимально можно взять 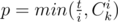 чисел с i единицами. Добавим p к ответу, а от t отнимем p·i. Отметим, что значения Cki нужно считать аккуратно — они могут оказаться слишком большими, и нужно не допустить переполнения.
чисел с i единицами. Добавим p к ответу, а от t отнимем p·i. Отметим, что значения Cki нужно считать аккуратно — они могут оказаться слишком большими, и нужно не допустить переполнения.
Можно показать, что сложность такого решения на один тест составляет не более O(log2n).
Осталось доказать необходимое утверждение. Идея доказательства ниже принадлежит rng_58 (авторское было заметно сложнее).
Решим задачу жадным алгоритмом с ограничением в k·m на общее число единиц. Полученное множество может не удовлетворять ограничению в m единиц на каждый разряд — тогда в некоторых разрядах количество единиц больше m, а в некоторых меньше m. Возьмём некоторый разряд X, в котором более m единиц, и некоторый разряд Y, в котором менее m единиц. Найдём строки, в которых стоит 1 в X и 0 в Y (допустим, таких строк x) и строки, в которых стоит 0 в X и 1 в Y (допустим, таких строк y). Понятно, что x > y. В каждой из x строк мы можем попробовать поставить 0 в X и 1 в Y — тогда полученная строка может либо остаться уникальной, либо совпасть с какой-то из y строк (но ровно одной). А поскольку x > y, точно найдётся одна из x строк такая, что в ней можно поменять местами цифры в разрядах X и Y и все строки останутся различными. Сделаем это. Теперь в разряде X стало на одну единицу меньше, а в разряде Y — на одну единицу больше. Это значит, что суммарное число лишних единиц в разрядах уменьшилось (т.к. в Y единиц не стало больше m). Таким образом, повторяя эту операцию необходимое число раз, мы сможем добиться того, чтобы в каждом разряде было не более m единиц.











Буду признателен, если кто-нибудь подскажет, почему не работает подсветка хэндлов пользователей.
А в предпросмотре отображает? У меня и в блоге и в комментарии отобразило.
"Главные действующие герои задач D(div 1) и B(div 2) — Chmel_Tolstiy и ivan.metelsky."
Скопировал текст из разбора — отображает и в предпросмотре, и в комментарии. В самом разборе, почему-то, не отображает ни там, ни там.
Если заново создать пост с полностью таким-же текстом как в разборе, то нормально отображает(по крайней мере в предпросмотре). Может там лишние символы стоят?
попробуй использовать тильду "~"
например [тильда]Chmel_Tolstiy даст Chmel_Tolstiy
Если после прочтения у вас остались какие-то вопросы, не стесняйтесь задавать их в комментариях — понятно, что разбор содержит только идеи и наброски решения задач, а не детальное описание.
Задача В(div 2) Если не ошибаюсь, то неверно написано нахождения количества инверсий, если не трудно, можно по подробней об этом, из-за этого и не сдал ее((
Одна инверсия — это пара слов, идущая не в таком порядке, как в условии задачи Лёши. Соответственно, после того, как мы перебрали подпоследовательность описания задачи из архива, содержащую слова из задачи Лёши, нам нужно посчитать количество таких пар слов, которые образуют инверсию. Поскольку в примере псевдокода индекс a отвечает за первое слово, b — за второе, c — за третье и d за четвёртое, то инверсии образуются, если a > b, a > c, a > d, b > c, b > d либо c > d. Проверяя каждый из этих случаев, мы получаем количество инверсий в подпоследовательности, которую мы сейчас перебрали.
Thanks for publishing editorial! There are some mistakes in text. It seems [user:] function is broken and is not working properly so that links to users are not created. Or is it a problem from my side and other users don't have any problems with it?!
I think there is problem in ur side because I can see the users in colors with their profile links ..Ofcourse ,Unless I am too late to answer , which I dont assume otherwise the blog author must have replied to u ..
There is a strange bug with Codeforces Markup which has been already reported to MikeMirzayanov. Anyway, I've fixed it in this blogpost by adding a couple of linebreaks :)
В задаче C(Div 1) я не понял что такое sumOddi. Может кто-нибудь объяснить поподробнее?
sumOddi — сумма всех oddj при 1 ≤ j < i (то есть сумма oddj для всех мостов левее платформы i). Если теперь вычислить sumOddj - sumOddi (при i ≤ j), мы получим максимальное количество переходов по мостам, которое можно совершить, начав на платформе i, закончив на платформе j и используя только мосты строго между этими платформами.
Спасибо за подробное объяснение.
Какая-то странная оценка асимптотики в задаче D. Почему там m·(...)?
UPD: сорри, перепутал обозначения — там все нормально.
Наверное, потому-что там для каждой задачи отдельно.
А, понятно — это я обозначения перепутал.
Задача B(div2). Подскажите, пожалуйста, сколько будет инверсий и как они выглядят?
4a b c d110 b c a b a d d d a aКоличество инверсий зависит от выбранной подпоследовательности.
Если, например, выбрать подпоследовательность
b c a d, то количество инверсий будет равно двум:b aиc a(эти пары идут не в том порядке). Если выбратьc b d a, то количество инверсий будет равно четырём:c a,b a,d a,c b. В каждой задаче нужно найти такую подпоследовательность, количество инверсий в которой минимально, и вывести номер задачи с самым минимальным количеством инверсий.i am still not able to understand the solution of Div 2 problem C. Can anyone please explain me in a more detailed way. Please :)
Can someone explain Div2- C. It is not clear for me too.
anyone please tell me what following line of code is doing
this line is from rng_58's solution of problem D.
Подскажите, пожалуйста, как вычислить количество инверсий заданной перестановки за линейное время.
имелось в виду количество инверсий? если да, то так: заведем дерево отрезков с добавлением в точке и запросом суммы на отрезке, изначально там все нули. Будем добавлять элементы перестановки в порядке возрастания. Если мы сейчас добавляем число на позицию i, то в дереве отрезков прибавим единичку к элементу i, и запросим сумму на отрезке [i+1, n] — так мы найдем количество инверсий (i,j), где i<j и p[j] < p[i]. Ну и нужно сложить все такие суммы.
Да именно, спасибо!
Можно еще с помощью сортировки слиянием, подобным образом:
В ходе каждой итерации сортировки у нас массив делится на 2 части. Тогда общее число инверсий — это количество слева + количество справа + количество в общем массиве ( когда левый элемент больше правого).
Тогда можно записать следующим псевдокодом:
Вот кстати 95% людей пишут Фенвика, а mergesort вроде бы проще, да и Кормен рекомендует...
Зависит от того, как кого учили, я до недавнего времени тоже фенвика писал все время.
Это за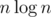 все-таки. Для количества инверсий можно еще использовать
все-таки. Для количества инверсий можно еще использовать  , а для поиска инверсии к перестановки, то есть такой перестановки q, что q·p = e, можно поступить следующий образом: запомним, куда переходит каждый элемент, то есть
, а для поиска инверсии к перестановки, то есть такой перестановки q, что q·p = e, можно поступить следующий образом: запомним, куда переходит каждый элемент, то есть 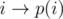 , а обратной будет перестановка
, а обратной будет перестановка 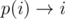 .
.
К примеру, p = (2, 5, 4, 3, 1)
25431
поменяем 2 строки местами, получим
25431
12345
отсортируем по первой строке
51432
Another solution for E?
If the problem can be solved by brute force why does it appear in tag of binary search and how to solve it using binary search :)
Which problem are you referring to?