Auto comment: topic has been translated by Um_nik (original revision, translated revision, compare)

What is the idea behind problem K?

Can anyone tell me how to solve I?

Full editorial in Russian

Short solution ideas:

A (author Um_nik) — just do what is written in statement

B (Um_nik) — One of the rectangle sides will be on one of triangle sides. If we'll fix that triangle side there will be no more than 2 rectangles. We can find them explicitly. Don't forget about traingles with big angle (>= 90 degrees). Solution can be written in rational numbers in Java/Python but double solution is also OK.

C (Tinsane) — iterate prime numbers, if the number of prime numbers our number have is small and current prime is big then the answer is NO.

D (Um_nik) — it is easy to construct path with length no more than 3. For shorter path write bruteforce starting from T (each number have small number of divisors, it will be fast).

E (sivukhin) — write stupid retrograde analysis, it will work in time. Can be optimised to O(n) using sime prefix sums.

F (sivukhin) — Let the sum of distances traversed by Alice and Bob be L. Then the answer is S / L

G (crassirostris) — just do what is written in statement. May look terrifying, but my solution in Python is easy 40 lines of code (and I'm not a master of Python). Be careful with integer (and even long long) overflow.

H (Um_nik) — every such function must be a permutation. Permutation can be decomposed to some cycles. We want all cycle lengths in our permutation be a divisor of k. Initially we have some cycles and chains, we can join chains and make cycles from chains. We can write an O(3ⁿ) DP on subsets but it will be too slow. Notice that chains of length 1 are special — it will lead to O(3^n / 2) and even O(2^n / 2n²) solutions. Also it can be solved with some smart bruteforces, one of them actually works for n up to 55.

I (kb.) — just do n iterations trying all the rules. Complexity will be O(n²m) which is not fast enough. But we can speed it up using bitsets. Also we can store a pointer to first missing pony in every rule, thus obtaining O(nm) solution.

J (Tinsane) — standard problem with some queries on segments. Let's find LCA (of two vertices) using sparse table, and the build another sparse table to answer queires. Complexity will be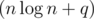 , but constant factor is quite large. I_love_Tanya_Romanova got AC with O(log²n) per query solution.

K (Um_nik) — if we can save at least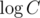 elements then we can get OR of all array, which is obviously maximal. So if 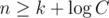then the problem is trivial. Now we'll solve two problems separately: bruteforce for small k and knapsack-like DP for small C.