Tomorrow is GP of Dolgoprudny which is prepared by my colleagues and me.
Hope, you'll like the problems which we can discuss here after the contest.
Also, we've prepared mini-tutorial which I'll post here after the contest too.
Good luck!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Tomorrow is GP of Dolgoprudny which is prepared by my colleagues and me.
Hope, you'll like the problems which we can discuss here after the contest.
Also, we've prepared mini-tutorial which I'll post here after the contest too.
Good luck!
| Название |
|---|



Кажется, провести опенкап вышло неплохим отвлекающим маневром :)
Mini editorial
My solutions for problems I had solutions.
Как решать L и O из див2? (О квадрате из прямоугольников и о сокращении дроби). Спасибо.
L. Начиная с последних цифр изменять отдельно числитель и знаменатель дроби. Каждый раз когда они увеличиваються — упрощать (делить оба на 2, 3, 5, 7 <10, т.к. A[i] и B[i] < 10), пока дробь становиться неупрощаемой.
Ничего не понял? Я вообще думал , что надо начиная снизу все время получать общие знаменатели и в конце вывести формулу. Но ничего не вышло.
Да, верно, так и надо. Только еще надо упрощать, например: 2/4 => 1/2.
O. Прямое решение: создать матрицу 301 x 301, заполненую 0. По двум осям (x, y) заполнить единичками. Далее рекурсия: 1) ищим уголки (в начале ровно один — x=1, y=1), 2) от каждого уголка засыпаем единичками прямоугольник двумя вариантами (повернутый и не). Посли засыпки 3 прямоугольников, проверяем от x=1, y=1 — засыпан ли квадрат.
К тому же перед посылкой забыл изменить 15 на 301, но получил AC. Потом взломал себя — код выдает YES на тест "
3 3\n3 6\n9 6\n" и NO на "30 30\n30 60\n90 60\n".Поясните пожалуйста как Вы делаете заливку на входном тесте 8 2 1 6 6 7 с каких уголков?
Заливка с аналогичным тестом (ideone, Perl). Переберая все возможные уголки с поиском по рекурсие.
Как решалась задача P. No Triangles ?
Надо вычеркнуть числа не являющиеся фиббоначи.
1 2 3 4 5 6 вычеркиваем 4 и 6 ответ 2
Спасибо. А почему именно их?
Уже понял. Из-за неравенства треугольника. Рассмотрим самое большое число Фибоначчи — fib[i], которое меньше, либо равно n. Оно не может быть стороной треугольника, потому что оно равно сумме двух предыдущих чисел фибоначчи: fib[i-1], fib[i-2]. А все остальные суммы будут меньше. Поэтому мы переходим к числу fib[i-1] и повторяем рассуждения.
Nice problem set. May I ask why do you make B with n = 104? I think it's more fair to have n = 5, 000 for O(n2) solution.
With n = 104, we should be extremely careful with the constant involved in the computation.
It was made to prevent solutions with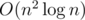 complexity. Sorry if you had to spend much time optimizing your solution.
complexity. Sorry if you had to spend much time optimizing your solution.
Can you provide the contest link please?