Given a bipartite graph with nonnegative edge weights, find a matching with maximum total weight (maximum number of edges is not required).
Example:
V = {1, 2, 3, 4}, E = {{1, 2}, {3, 4}, {2, 3}}
w({1, 2}) = 1, w({3, 4}) = 1, w({2, 3}) = 10
Optimal solution: {{2, 3}}
A friend suggested the following solution:
- Ignore weights and find maximum cardinality bipartite matching MCBM.
- For each
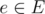 , define w'(e) = BIGVALUE - w(e).
, define w'(e) = BIGVALUE - w(e). - Find mincost flow for f = 1, 2, 3, ..., MCBM with respect to new weight function w'. Output the minimum.
Will that work? Is there any faster solution?











https://www.topcoder.com/community/data-science/data-science-tutorials/assignment-problem-and-hungarian-algorithm/
I actually was not able to quickly find the answer to the posted question in the article posted above. Where do they discuss this problem there?
Even if it has good solution, I figured I will tell how to adjust regular min-cost max-flow to solve your problem. There are two problems here:
1, MCMF finds a flow of minimum cost, not maximum cost;
Consider the mincost maxflow algorithm that runs Dijkstra with potentials on each iteration to find a path to relax. We can easily solve both of the above problems with very slight adjustments:
To find the flow of maximum cost instead of minimum cost it is sufficient to change edge weights with their negatives. The problem here is that Dijkstra doesn't run very well on graphs with negative weights. This problem can be easily solved by first running Bellman-Ford once, finding shortest paths to all the vertexes, and initializing potentials with those shortest paths. Now from perspective of Dijkstra all the edges are non-negative;
To find the maximum cost flow, not maximum cost maximum flow (as in, to make MCMF optimize for cost instead of optimizing for flow and then for cost) just change the stopping condition to stop when the path Dijkstra finds has negative sum of weights, instead of stopping when Dijkstra can't find a path at all. It's easy to show, that each new path Dijkstra finds has smaller total weight than the previous path, so the moment you see a negative path, you will only decrease the cost after that.
I think the first poster meant that if we complete the graph by adding edges of weight 0 where there is no edge, then the problem being solved is exactly the one solved by the Hungarian algorithm.
I wouldn't say that he made it very clear (the fact that if you add zero-weight edges then what hungarian algorithm finds is what the OP wants). I would assume that OP knows about the hungarian algorithm, so the actual answer to his question is in your comment, not in the link above.
I'm curious if people downvoting me exclusively because my solution is inferior to Hungarian algorithm with extra edges, or if I have some factual errors too?
NOTE: I am not answering the question, just correcting some of your statements.
Just multiply all costs by -1.
Actually, given some F, MCMF can find the minimum cost for transmitting exactly F units of flow.
Yes, this is what I am suggesting.
But we do not know F in advance in this particular problem.
We can increase F by one until the shortest path in MCMF residual graph is non-negative (or does not exist).
That is what I'm suggesting in the original comment