How to determine whether a number is a product of consecutive primes? The number can be at max 10^14. Any hints is really appreciated.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 16:05:53 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











If the number is a product of 2 consecutive primes then how large can those primes be?
What is the maximum number of consecutive primes you can multiply so that the product is within 10^14?
Assume p and q are the required consecutive primes which satisfy p*q=n. Since p is not equal to q, p has to be less than √n and q has to be greater than √n. Also, for them to be consecutive, p has to be the largest prime number less than √n and q has to be the smallest prime number greater than √n.
Edit: The above solution checks for 2 consecutive primes. The above solution extended for k primes is explained here.
If you are only looking for 2 consecutive primes, then find the largest prime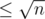 and the smallest prime
and the smallest prime 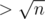 and check if their product is equal to n. You might be able to make a similar idea work for any number of consecutive primes, though it seems tricky.
and check if their product is equal to n. You might be able to make a similar idea work for any number of consecutive primes, though it seems tricky.
If it's a variable number of consecutive primes, you can try to binary search for a k-size subarray of primes that matches, for k ≥ 2. Note that k < 13 https://oeis.org/A002110. You would also have to check is n is prime.
If there is only one query, you can find all primes in [2, 107], find the smallest prime that divides N and check the product easily. Be careful when N is a prime number.