Сначала расположим задачи по сложности, как предполагалось авторами: A, D, B, C, E. Теперь разберем задачи по порядку следованию в соревновании.
Эта задача носила технический характер. Сначала нужно было удалить все вхождения слова WUB в начале и в конце исходной строки. А затем распарсить оставшуюся строку, разделяя токены словом WUB. Пустые токены нужно было пропустить. Ограничения были небольшие, реализовать это можно было как угодно.
В этой задаче можно было написать поиск в ширину. В качестве состояния можно взять следующую четверку: количество оставшихся стопок, а также три строки, которые обозначают три крайние правые карты на трех крайний стопках. Соответственно мы имеем два перехода в общем случае, когда перекладываем последнюю карту на 1, либо на 3 влево. Если количество стопок в какой-то момент окажется равным 0 выводим YES, иначе NO. Состояний O(N4), переходов 2, итого временная сложность решения O(N4).
208C - Контрольный пункт полиции
В данной задаче для каждой вершины отдельно посчитаем искомую величину и найдем среди них максимальную. Для этого для каждой вершины v посчитаем две величины: cnt1[v] и cnt2[v] — количество кратчайших путей из вершины v в n-ую вершину и 1-ую вершину соответственно. Чтобы это сделать, нужно построить граф кратчайших путей и посчитать на новом графе динамику (поскольку полученный граф будет ациклическим). Чтобы построить граф кратчайших путей, нужно оставить в графе только полезные ребра, предварительно запустив, например, поиск в ширину из вершин 1 и n соответственно.
После того, как величины cnt1[v] и cnt2[v] посчитаны, переберем все полезные ребра исходного графа (u, v) и к вершинам u и v прибавим величину (cnt2[u] * cnt1[v]) / (cnt2[n–1]), которая является вкладом этого ребра в искомую величину для вершин u и v. Заметим, что величина (cnt2[n–1]) — это общее количество кратчайших путей от вершины 1 до n. Все величины, которые были упомянуты, можно посчитать за размер исходного графа. Вычислительная сложность решения O(N + M).
208D - Призы, призы и еще раз призы
В этой задаче после каждого нового получения очков нужно было жадно набрать себе призов. Для этого переберем призы, начиная с самого дорогого, и попробуем взять как можно больше. Если у нас cnt очков, а текущий приз стоит p очков, то мы можем получить 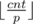 призов. Получаем простое решение за O(5 * N).
призов. Получаем простое решение за O(5 * N).
В задаче нам задан набор ориентированных вниз корневых деревьев. Сначала обойдем поиском в глубину каждое дерево в отдельности и перенумеруем вершины. Пусть размер поддерева вершины v — cnt[v].Тем самым получится, что все потомки вершины v, учитывая саму вершину v, будут иметь номера в отрезке [v;v + cnt[v]–1].
После этого будем обрабатывать запросы (v, p) по очереди. Поднимемся из вершины v запроса на p вершин вверх к корню, используя двоичный подьем, похожий на поиск lca в дереве. Пусть мы пришли в вершину u. Если у вершины нет предка на расстоянии p, сразу выводим 0, иначе нужно посчитать количество потомков полученной вершины u, которые имеют ту же высоту в дереве, что и вершина v.
Для этого, для каждой высоты выпишем в отдельный массив номера всех вершин с этой высотой. Тогда для ответа на запрос, нужно узнать, какие из вершин этого массива являются потомками нашей вершины u. Для этого можно бинарным поиском в этом массиве выделить отрезок подходящих вершин (поскольку мы знаем номера потомков вершины u) и посчитать их количество. Вычитаем из этого количества единицу (саму вершину v) и получаем ответ. Вычислительная сложность решения O(Nlog(N)) — двоичный подъем и бинарный поиск.











В задаче E есть еще одно классное решение. В Петрозаводске на саратовском контесте я узнал об этом приеме.
Сохраним все запросы и запустим dfs. Для каждой вершины будем хранить deque, где по h-ому индексу лежит количество потомков на глубине h (на запросы с помощью такой структуры ответить довольно легко).
Теперь главная фишка: при подсчете этой deque для текущей вершины надо не создавать новую deque, а переприсвоить ее, взяв ее от того потомка, где эта deque имеет максимальный размер (т.е. где поддерево имеет максимально возможную глубину). Именно переприсвоить, а не скопировать. Оператор '=' копирует! Т.е. надо работать с указателями.
После этого для этого потомка уже ничего нельзя посчитать — его deque испарилась — текущая вершина ее покалечила — однако все, что надо, мы уже посчитали, когда находились в этом потомке, одним dfs-ом ранее. Для остальных потомков просто пройдемся по их deque-ам и выполним что-то типа current[h+1] += child[h];
Из-за магии время работы этой штуки O(NlogN).
P.S. код: http://codeforces.net/contest/208/submission/1933305, вроде бы достаточно читабельный
Это не магия. Это простое соображение следующего вида.
Если мы хотим узнат от каждой вершины какую-то информацию, пропорциональную размеру её поддерева R(v) (в данном случае — R(v) это вектор, где R(v)[d] есть количество вершин глубины d в поддереве вершины v), и мы умеем сливать информацию R(v1) и R(v2) двух детей вершины v за размер меньшей из них (нам нужно пройтись по вершине меньшего поддерева и проприбавлять к большему значения во всех ячейках за O(size(R(vmin)))), то в итоге всё будет работать за O(n log n).
Это очень просто понять — давайте считать, сколько раз каждая величина будет участвовать в "приливании к большему соседу". В нашем случае — сколько будет операций +=. После каждой операции += размер того вектора, в котором лежит число, увеличивается минимум вдвое. А значит всего не более log n раз каждое число будет менять тот контейнер, в котором оно лежит. Значит всего асимптотика не более O(n log n).
И это работает в гоооораздо более широком диапазоне применений — необязательно использовать дек. Можно хоть мапы примёрдживать друг к другу. Вот эта идея "примёрджим меньшее к большему" как-то очень популяризовалась после последней IOI — она очень мощная но по умолчанию только в оффлайне — чтобы сделать её онлайновой нужно прикручивать персистентность.
верно говорите, такое решение тоже было, причем авторское от Gerald)
На куда более простое интересное оффлайновое решение я наткнулся просматривая код Rubanenko.
Идея в том, что можно просто обходить дерево в глубину и делать только a[depth]++, и если взять разность значения a[x] на момент выхода из поддерева и на момент входа получится сумма на поддереве.
И сложность O(N).
1929766(если бы не на паскале было бы вобще четко)
Как и у меня. Но сложность всеравно не линийная изза двоичного подьема.
Да, и правда, в этом решении не линия, но можно опять же оффлайн предка в сумме за O(N) находить.
Я такое решение на контесте не успел написать, сдал в дорешивании: 1933222
Правда, чтобы асимптотическая быстрота вашего решения имела смысл, необходимо избавляться от стл;(
<зануда-моде>
Это, всё же, будет не O(N), а O(αN)
</зануда-моде>
UPD: Nevermind... спать надо в два часа ночи, а не умничать, походу.
Можно подробнее, что такое O(αN) и откуда оно тут? по мне так O(N) получается...
Нужного предка можно обычном стеком находить, зачем нам обратная функция Аккермана?
Так. Мне всегда казалось, что классический алгоритм поиска LCA в оффлайне — это тот, который самый простой и с СНМом. А как делать со стеком?
Ну нам же не нужен LCA, у нас задача проще: нам нужен k-ый предок просто, а это делается очевидно дфсом+стеком: 1934524
Ааа, понял! Вот почему не стоит комментировать в два часа ночи. — такую фигню напишешь, а потом стыдно :-)
Есть какая-то оптимизация СНМа, с которой алгоритм Тарьяна работает за O(1) на запрос. В Википедии указана статья, где это описано.
Оуу.. да, там код даже на паскале можно поопрятней сделать.
Кстати, идея не моя, она принадлежит Sereja. Придумал он это как-раз на трансляции финала ВКОШП-а. Я тогда онлайн sqrt-декомпозицию сдал.
Реализация этой идеи у dalex немного через универсальный интерфейс.
Правильно примерно так:
P.S. сорри за не туда прицепленный коммент.
Задача Е со ВКОШПА + двоичный подъем
Можете B объяснить по подробнее динамикой?
Определим функцию
bool ok(int len,string a,string b ,string d ).ok(len,a,b,c)=true, если можно собрать пасьянс из колод с верхними картамис[1],c[2],c[3]..c[len-3],a,b,d.Если можно положить и d на b, и d на c[len-3]:
Если можно положить d только на b:
Если можно положить d только на c[len-3]:
Если d некуда положить:
Случаи с len<=3, нужно рассмотреть отдельно. После нахождения ok(len,a,b,d), запомним результат и в следующий раз просто вернем его.
Какой ещё N^2 в 208D? Решение за чистое Θ(5N).
да да, второе n маленькое)
Контест понравился, но претесты, по задаче Б, УГ.
Хорошо, что на сервере стоит 8я вижуалка. Это помогло мне безболезненно отловить баг в коде для D, так как у себя на 10й примеры проходил, а на сервере WA#1 :-)
Здравствуйте, можно ли решить задачу 208B — Пасьянс вложенными циклами?
легко
например
можете ответить что означает wrong answer 1st words differ — expected: 'ABC', found: 'ABC' http://codeforces.net/contest/208/submission/1938233
Символ с кодом 0 напечатался. В веб-интерфейсе его, разумеется, не видно.
Поставьте ключ
{$R+,Q+}. У вас рантайм, который как-то странно обработался по-моему. В результате вывелись непробельные символы с маленькими кодами, которые не отображаются.офигеть, ну объясните идиоту как делается Б. Я не пойму откуда вы 4 измерения берете!Как перекрываются подзадачи в динамике?
Честно говоря, чувствую себя совсем не в теме — что за модная структура хранения деревьев на двумерном массиве в задаче Е? Я просто делал совсем наивное хранение в двумерном массиве, а как начал чужие коды глядеть, постоянно на мифические массивы [18][10^5] натыкаюсь :) Подскажите, что за тема?
p[i][j] это (1<<i)-ый предок j-ой вершины. Потом из этой штуки можно какого хочешь предка восстановить.
Это не способ хранения деревьев. Это, как сказал dalex — способ за O(logN) достучаться до своего предка, где N — расстояние до предка. Подобная идея используется в разряженных таблицах для RMQ: погляди здесь и собственно сам двоичный подъем
На счёт задачи 208B — пасьянс. Максималиная глубина поиска будет n. При каждом погружении появляется до 2 переходов. Выходит состояний будет O(2^n),но не O(n^4) и BFS не проидёт по времени и памяти. Вот пример моего решения через BFS, который дал RE на тесте 8:
Прочитайте, что надо взять в качестве состояния.
Вы знакомы с динамическим программированием? Суть в том, что ваш BFS будет посещать одно и то же состояние множество раз. Это решение превратится в ОКовое, если после обработки вершины вы будете помечать, что вы в состоянии, соответствующем этой
colodaпобывали, а перед тем, как добавлять в очередь вершину, вы будете проврять, что такаяcolodaещё не посещена.+1.Спасибо большое за подсказку.Ваш алгоритм мне понятен.Я чуть-чуть знаком с ДП ( в моём представлении ДП связано с комбинаторикой и рекуррентным соотношением типа f[i]=f[i-1]+f[i-2] или f[i][j]=...). Придумать алгоритм с использованием ДП, а уж тем более реализовать ДП мне не под силу. ДП изовсех сил пытаюсь обходить ( никогда не получалось, если засчитывают только полное решение ).
Can somebody help me for the E problem. How do I calculate the pth ancestor of some vertex. Simply climbing till the root gives TLE. The Editorial says to use the LCA algorithm. How do I use the sparse table to get the pth ancestor?
you can store the 2^i'th ancestor of each node as u do in binary . now for pth ancestor ,visualize p in binary like suppose p i 62 then 62 can be breaked as 32+16+8+4+2 thus u can find it's 32th parent in O(1) as u have already stored then it's 16 th ancestor and so on....it is just like finding x**y in logn time..
My approach is that I am keeping count of pair<node,level> for every node during HLD preprocessing. Then for each query I see its pth ancestor and total number of pair<pth ancestor,pth level> but it giving me wrong ans. Why can you help me?
By Errichto, a great place to learn from !!
An other approach on 208E blood cousins without usage of LCA or binary search: We store the queries offline in a list on the appropriate cousin nodes and then we traverse with a dfs to update level of every node and move queries to the ancestor requested for every cousin. You can use a list to store multiple queries on every node.
A second dfs will parse and update the queries: when every node is recursively pre order processed, it pushes the count of children found on next levels (only on levels required by a query) and zero them. The dfs will continue to the children and uppon return, the final countouts would have been calculated. Previous pushed countouts are restored and updated.
O(N+M) reading O(N+M) first DFS (DFS on N nodes + move M queries to ancestor) O(N+2*M) second DFS (DFS on N nodes + push M counters, process M queries, pop M counters) O(M) print results
Overal complexity O(N+M).
Print results in order of appearance in test file and voila.
Nice
Can you please send a clear code for this concept. It seems interesting.
Hello, For 208E — Blood Cousins problem, could you please explain as to how a binary search helps in counting the number of nodes for the target level. I am referring to the last paragraph of the editorial "count the number of descendants of vertex u on the same height as vertex v"
Thank you in advance.
You can use the concept of discovery time and finish time.If we know the distance of node x , let it be a , then distance of all those nodes will be a + p. For every distance d , we will push all the node's discovery time and finishing time whose distance is d. Now , according to properties of dfs, all the nodes which are in subtree of node x will have discovery time > discovery time of x, and finishing time <= finishing time of node x. Since , we also know that all those nodes are at distance a + p. We will go to that distance vector and find number of nodes which has the above mentioned property. For more clarity, you can check out my Submission :)
Thank you for quick response. Now, I am trying to understand as to how to apply the concept of Discovery/Finish time in trees.
I will keep you posted incase I have any doubts.
Thanks again :)
That part is well explained in CLRS. You might want to take a look at it.
Will LCA work in E ?
LCA in E?
LCA in E?