Topcoder SRM 707 - Codeforces

→ Обратите внимание

До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »

*есть доп. регистрация

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	3993
2	jiangly	3743
3	orzdevinwang	3707
4	Radewoosh	3627
5	jqdai0815	3620
6	Benq	3564
7	Kevin114514	3443
8	ksun48	3434
9	Rewinding	3397
10	Um_nik	3396

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	156
8	TheScrasse	154
9	Dominater069	153
10	nor	152

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя cgy4ever

Topcoder SRM 707

Автор cgy4ever, история, 8 лет назад, По-английски

Topcoder SRM 707

Time: 9:00 pm EST Monday, January 30, 2017

Calendar: https://www.topcoder.com/community/events/

cgy4ever
8 лет назад
53

Комментарии (48)

Показать архивные | Написать комментарий?

cgy4ever

8 лет назад, # |

Update: we added one more SRM on Jan 11th and moved the SRM on 14th to 21st.

So we will have 3 SRMs in January! See details: 705, 706, 707

→ Ответить

cgy4ever

8 лет назад, # |

+41

SRM 707 will start in 24 hours!

→ Ответить

animeshf

8 лет назад, # |

Could people describe some clean solutions for Div 1 250?

→ Ответить

cegprakash

8 лет назад, # ^ |

I was thinking in terms of BFS initially couldn't get any clue.. Then tried zig zag patterns. No idea at all :(

→ Ответить

Morphy

8 лет назад, # ^ |

Is always possible to generate a pattern of the following form:

→ Ответить

animeshf

8 лет назад, # ^ |

Thanks! I guess this can be done in O(N²) too, but O(N⁴) seems safer to code for TopCoder SRMs.

→ Ответить

cegprakash

8 лет назад, # ^ |

This was my intuition. But how to find the rows and cols required and the zig zag pattern?

Note that the above pattern does not have any up direction moves.

We should also consider the symmetric case where we have to do a pattern with no left direction moves.

→ Ответить

animeshf

8 лет назад, # ^ |

Take a 50 * 50 grid with all cells "Safe". Note that the initial shortest path is 98. Handle K < 98 separately.

Then, whenever you are forced to move one step left/up, you increase the shortest path by 2. Thus, if you block enough cells you can make any even number in the range [100, 1000].

For odd K, use a 49 * 50 grid and repeat the same process.

→ Ответить

cegprakash

8 лет назад, # ^ |

I don't understand. How do u decide where to place the walls?

→ Ответить

animeshf

8 лет назад, # ^ |

Suppose your grid is n * m. You place it in the following order :-

(0, 1) (1, 1) (2, 1) ... (n - 2, 1)

(n - 1, 3) (n - 2, 3) (n - 3, 3) ... (1, 3)

(0, 5) (1, 5) (2, 5) ... (n - 2, 5)

and so on....

Basically you're forcing an up movement here and constraints are small enough for you to compute the current shortest path after each addition.

→ Ответить

george24601

8 лет назад, # ^ |

How to prove that this zig-zag approach gives the maximum k, i.e., it gives the maximum number of left steps + up steps?

→ Ответить

animeshf

8 лет назад, # ^ |

What do you mean by maximum number? Restating what I said earlier, every "up" movement that you make increases your shortest path by 2, so if K is even and n + m - 2 is even, then you will reach K by forcing sufficient number of "up" movements. The case where K is odd is analogous, just make sure that n + m - 2 is odd.

→ Ответить

animeshf

8 лет назад, # ^ |

Here is some code for reference.

→ Ответить

george24601

8 лет назад, # ^ |

← Rev. 2 →

Ignore this comment

Thanks for the reply.

"if you block enough cells you can make any even number in the range [100, 1000]."

Say for a 50 * 50 grid, how to prove that 1000 is the upper bound, and not something higher?

In other words, how to prove max number of "up" movements we can force on a board?

→ Ответить

KADR

8 лет назад, # ^ |

It doesn't. For instance, there's a pattern which can give up to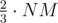 $\text{[math]}$ steps but it's too complicated for 250.

→ Ответить

george24601

8 лет назад, # ^ |

Ah I see why I was confused, I didn't pay attention to k <= 1000 constraint. Silly me!

Thanks a lot for your help!

→ Ответить

King_George

8 лет назад, # ^ |

-6

Could you please share with us how to make that pattern?

→ Ответить

Chelly

8 лет назад, # ^ |

← Rev. 2 →

+26

→ Ответить

SarvagyaAgarwal

8 лет назад, # |

Solution for Div2 500 and 1000 ? everybody failed Div2 500 .

→ Ответить

antonio.deluna

8 лет назад, # ^ |

There must be a mistake in the system test for Div2 500

→ Ответить

SarvagyaAgarwal

8 лет назад, # ^ |

Ratings are already updated though .

→ Ответить

yassin_

8 лет назад, # ^ |

Look at the systest, test 121 is wrong, I'm sure

→ Ответить

Hiasat

8 лет назад, # |

← Rev. 2 →

+22

There is an invalid test case in Div2-500

{{"...", ".#.", "..#"}, 4}

Expected (System test output): "DDRR"

Received (My Output): ""

Answer checking result: There exist a solution, but your output is "".

→ Ответить

cgy4ever

8 лет назад, # ^ |

← Rev. 2 →

Yes, we are fixing it.

Sorry for the delay.

Update: Fixed now.

→ Ответить

CodeItLikeAidos

8 лет назад, # ^ |

Return "Exists" if there is at least one cross on the given board. Otherwise, return "Does not exist". Note that the return value is case-sensitive.

Exist — Exists. I couldn't find bug around 30 minutes. System expected "Exist".

→ Ответить

AM51

8 лет назад, # ^ |

Please check my solution (Handle — AM51) . System tests are passing but someone challenged the solution before . Are you also reconsidering the challenges that might have been made with wrong cases ?

→ Ответить

P___

8 лет назад, # ^ |

How did it affect challenge phase in div2?

→ Ответить

zscoder

8 лет назад, # |

What's the correct way to solve Div 1 450?

→ Ответить

abcdef6199

8 лет назад, # ^ |

← Rev. 2 →

After applying K multiply operations and L add operations, S can be express in the form:

S * B^K + A(B^p1 + B^p2 + ... + B^pL) where pi < = K

Iterate K from 0 to 64 (or a bit bigger), consider remain = (T - S * B^K) / A, we'll try to express this as sum of power of B. This can be done with a simple greedy.

And make sure to check the case B = 0 first. I failed because of this :(

→ Ответить

zscoder

8 лет назад, # ^ |

I actually checked the case B = 0 wrongly. I didn't realize you can jump back to 0 if B = 0 -_-

→ Ответить

Shadek

8 лет назад, # ^ |

← Rev. 2 →

Is there any extra constraint like

p1 >= p2 >= .. >= PL=1

if we consider p1 is largest among them.

→ Ответить

abcdef6199

8 лет назад, # ^ |

It doesn't matter. Just 0 ≤ P_i ≤ K will do.

→ Ответить

SarvagyaAgarwal

8 лет назад, # |

approach for Div2 1000 ?

→ Ответить

egor.okhterov

8 лет назад, # |

← Rev. 2 →

Can anyone help me understand one thing.
How does the following code may result in segmentation fault for the following input:
{{".#...", ".#.#.", ".#.#.", ".#.#.", "...#."}, 3000}

Div2 500

#include <iostream>
#include <string>
#include <vector>

int n, m;
bool cell[50][50];
char p[3000][50][50];

int dr[4] = { 1, 0, -1, 0 };
int dc[4] = { 0, -1, 0, 1 };
char dir[4] = { 'D', 'L', 'U', 'R' };

bool valid(int r, int c) { return r >= 0 && r < n && c >= 0 && c < m && cell[r][c]; }

void dfs(int r0, int c0, int steps)
{
    if (steps > 3000 || !valid(r0, c0)) return;

    for (int i = 0; i < 4; i++)
    {
        int r = r0 + dr[i];
        int c = c0 + dc[i];

        if (valid(r, c) && !p[steps][r][c])
        {
            p[steps][r][c] = dir[i];
            dfs(r, c, steps + 1);
        }
    }
}

struct StepsConstruct
{
    static string construct(vector <string> board, int k);
};

string StepsConstruct::construct(vector<string> board, int k)
{
    n = board.size();
    m = board[0].size();
    for (int r = 0; r < n; r++)
        for (int c = 0; c < m; c++)
            cell[r][c] = board[r][c] == '.';

    dfs(0, 0, 1);

    int r = n - 1;
    int c = m - 1;
    if (!p[k][r][c]) return "";

    int id[256];
    id['U'] = 0;
    id['D'] = 2;
    id['L'] = 3;
    id['R'] = 1;

    string ans;
    while (k > 0)
    {
        int dd = p[k][r][c];

        ans.push_back(dd);
        r += dr[id[dd]];
        c += dc[id[dd]];
        k--;
    }

    reverse(ans.begin(), ans.end());
    return ans;
}

I cannot reproduce that problem locally and I get the correct output.

→ Ответить

CodeItLikeAidos

8 лет назад, # ^ |

array p has maximal index 2999 and steps variable can be 3000.

→ Ответить

egor.okhterov

8 лет назад, # ^ |

Thank you, now passed all systests ;(

→ Ответить

pakhandi

8 лет назад, # |

← Rev. 2 →

+15

Screencast-HackPhase

→ Ответить

selfcompiler

8 лет назад, # |

Can anyone please explain DIV 2 500 problem ?

→ Ответить

SarvagyaAgarwal

8 лет назад, # ^ |

The way i solved it : Write a recursive function bool canSolve(int row,int col,int stepsLeft) which tells you if it is possible to reach cell (n-1,m-1) from cell (row,col) in exactly stepsLeft steps . Transitions are pretty straightforward , just recurse on all 4 adjacent cells .

→ Ответить

selfcompiler

8 лет назад, # ^ |

where to stop that recursion when steps left becomes zero ?

→ Ответить

SarvagyaAgarwal

8 лет назад, # ^ |

Base Case : if(stepsLeft == 0) { return row == n-1 && col == m-1 ; }

→ Ответить

selfcompiler

8 лет назад, # ^ |

← Rev. 3 →

can we have this approach 1. find the shortest path such that ((K-pathlength)==even_number) 2. print that path 3. repeat last two consecutive characters (K-pathlength) times .

→ Ответить