| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
2 января 2016 в 02:17 (время московское) открылся первый этап SnarkNews Winter Series 2017. Как и несколько предыдущих серий, SNWS-2017 пройдёт на системе Яндекс.Контест. Опубликовано расписание серии.
По просьбам участников отдельно публикую ссылку на вход в первый раунд. Здесь же по окончании раунда в соответствии с расписанием можно будет обсудить задачи первого раунда.
Что со вторым раундом? На сайте ссылка есть, но Яндекс пишет "У вас нет прав просматривать это соревнование".
Check now?
Теперь работает
tourist, ты в D писал корневую?
Мне до tourist-а далеко, но я сдал в дорешку корень лог. Зашло за 3 секунды из 10 даже без подгона размера блока.
Было обидно, дифф с решением с контеста -- четыре символа.
Мне было интересно, нельзя ли придумать что-то за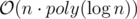
, мало ли.
UPD: А лог под корнем или снаружи?
Знаю, что zemen и Endagorion писали какие-то деревья отрезков, но никто из них в итоге не довёл до решения. Так что мне тоже интересно.
Ну я тоже написал какое-то дерево отрезков, и тоже не довёл до ОКа — получил ТЛ на контесте.
Давай хранить в каждой вершине мапу — сколько и каких чисел есть на данном отрезке. Поддерживаем инвариант, что в "некоторых" вершинах эта мапа корректна. Кроме мапы проталкиваем вниз число — на этом отрезке нужно сделать min= с числом x. Когда приходим в вершину, просто берем честно все числа, которые больше, чем x, и склеиваем их в x (суммарно вроде таких операций должно быть не очень много, т.к. либо одно число за лог, либо склеились два числа и ~ навсегда (нет, но чтобы их разъединить нужен будет еще запрос на более коротком отрезке)). Кроме того, когда приходит запрос "сделать новое min= на каком-то отрезке", разбиваем этот отрезков на вершины в дереве, в каждой из них все числа большие x склеиваем в x, и кроме того, в каждом из предков этой вершины повторяем те же самые действия. Таким образом, после обработки запроса корректны все мапы, в которых максимальное число не больше xv соответствующей вершины.
Это похоже на какой-то log3, можно ускорить минимум на один логарифм если вместо мапы хранить отсортированные массивы со всеми числами, которые когда-либо появлялись на этом отрезке (их тоже не много, n log). На случайных тестах на 10^6 даже укладывается в десять секунд.
Под корнем. Стандартная штука с блоками размером по корню, в каждом блоке отсортированный массив.
Уведомления работают! :)
Да, у меня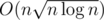
.
Я написал в задаче B суффиксный массив и получил TL. Потом в дорешке добавил отсечение "брейкнуться, если количество классов эквивалентности уже равно n" и получил AC. Это какая-то особенность местных тестов? Или наоборот, известный хак? Потому что вроде бы на строке из всех одинаковых букв процесс построения должен был затянуться до максимума.
Я всегда это отсечение пишу, ровно потому, что оно иногда спасает в случае не очень сильных тестов. Здесь, видимо, именно такая ситуация.
А ты же знаешь, что эту задачу можно без суффструктур решать?
Знаю, но на контесте не придумал.
Просто совсем немного удивительно, что для стандартного суффиксного массива худшим случаем оказывается рандомная строка, а не строка из одинаковых букв. Может, конечно, дело в том, что в случае строки из одинаковых букв почти последовательный доступ к памяти.
Почему худшим? Как раз если отсекаться, когда количество классов эквивалентности стало равно |S|, то на случайной строке ты почти сразу остановишься, потому как для сравнения любых двух суффиксов достаточно малого количества символов.
Под стандартным я имел в виду e-maxxовский вариант, который без этого отсечения :-)
Только что попробовал на задаче X случайную строку и строку из одинаковых букв, и оно все-таки на случайной работало немного медленнее даже с отсечением. А без него вообще 2.3 против 0.4.
Как решать C и F?
C: если ответ существует, то среди любых трех точек хотя бы две лежат на одной прямой. Переберем пару из первых трех точек и для каждой такой пары проверим, можно ли построить ответ.
А вообще на контесте у меня зашло решение "на любителя": пока не нашли ответ и не превысили некоторого порога времени (TL — 0.1 секунды), выбираем две случайные точки и проверяем, не нашли ли мы ответ. Нетрудно заметить, что если ответ есть, то он найдется довольно быстро :)
В C есть забавное рандомизированное решение: выберем две случайные точки и предположим, что одна из прямых проходит через них. Тогда легко проверить, правда ли не попавшие на эту прямую точки лежат на некоторой другой прямой. Если решение существует, то вероятность успеха >= 1/2.
F: ответ min(sumA / 2, sumA - maxA)
Почему: рассмотрим тупое решение, на каждой итерации будем брать 2 самых популярных предмета, тогда в конце останется один вид, в количестве X > = 0. В случае X = 0, 1 — ответ это sum / 2, в случае X > 1 это остаток от самой популярной кучки (причем ее изначальный размер больше половины от суммы), а значит все остальные предметы мы ставили с предметами из этой кучки, в таком случае ответ — sumA - maxA.
Третий раунд не работает, ситуация как была со вторым раундом "У вас нет прав просматривать это соревнование".