rofi93's blog

Help needed for a data structure problem
By rofi93, history, 8 years ago, In English

Problem: You are given an array consisting of n elements and q queries in the form of [L,R]. You have to output the maximum occurrences of a number in the segment [L,R] for each query.

How to solve these kind of problems using Segment Tree ?? I can solve this using sqrt decomposition, but got stuck trying to solve using segment tree.

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Still thinking about how you would do it with a segment tree, but here is a way you can do it in log n:

Store each number in an array of vectors, with the array indexed by each value in the input array. (You can use a map if values are very large.) In the vector you store the index of the respective value. You can binary search for the lower bound and upper bound of the segment in the vector and subtract their indices to get the answer.

The problem is that update queries are slow.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Wouldn't that output just the occurence of a particular number in the segment? But I thought he asked for the maximum frequency of all possible numbers in that segment..

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh...Seems like I misread the problem :/

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        May be i couldn't describe the problem well enough. I want to find the mode number (most frequent number) and the times it occurs in the given segment.

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Maybe I'm misunderstanding the question, but wouldn't you need to check all (up to N) numbers after doing this?

    rofi93, what is your sqrt decomposition solution? The best solution I see is O( ( N + Q ) sqrt N log N).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You can do it using MO's algorithm with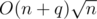 complexity. Let's compress coordinates and store for each number it's frequency (easy to update), and for each frequency list of numbers with this frequency in linked list. Because it's linked list we still can do updates in O(1) time, because we can store pointers for all numbers and find number in linked list in O(1) time and move element to other list in O(1) time. Now we just need to find list with maximal frequency which is not empty. Key idea is if we changed one element (like we do in MO's algorithm), answer can change only by 0, 1, -1. So if last answer was x, we just need to check if x — 1, x, x + 1 lists are not empty.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      My sqrt decomposition solution is O((N+Q)sqrt N).

      → Reply
»
8 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Found a link to similar discussion here. http://codeforces.net/blog/entry/19710?#comment-245484

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Read the solution for problem PATULJCI. I think that is what you need.

→ Reply