Hi everyone!
Thank you for joining Weekly Training Farm 19. The solution codes will be uploaded later.
Congratulations to:
Problem A. Aligned Text
This problem is equivalent to finding the longest arithmetic progression of a given set S. We can always enumerate the common difference w and use another loop to find the maximum length.
Problem B. Bitcount
If we want to count something that can be represented as a sum of values taken within an interval [a, b], we can always translate them as count([a, b]) = count([0, b]) - count([0, a - 1]). Usually this will make the implementation easier (and safer).
Moreover, in this problem, we can even deal with each binary digit separately. Hence, given an upper bound m ( = b or = a - 1) and a position 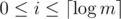 , we can focus on counting the number of 1-bits in the i-th position between 1 and m.
, we can focus on counting the number of 1-bits in the i-th position between 1 and m.
Problem C. Crossing River
There are "forward" methods and "reversed" methods. The "forward" idea is to identify dp[i] to be the smallest possible jumping gap from the left river bank to the i-th rock. However, the table is not easy to build in  time. Although I believe it is achievable using
time. Although I believe it is achievable using set iterators, but no one use it during the contest =)
The key to this problem is to use the "reversed" idea: binary search. We first guess an answer m and then decide if the frog can cross the river with jumping distance no more than m. There are several way to do this. The first idea (coincident to the author's solution) is to use the sliding window technique: keeping all reachable rocks within the range [i - m, i - 1]. If any of these rocks has value less or equal to ai, then the i-th stone is reachable. We can use a deque to achieve linear time testing given m.
The second idea is to first sort the rocks according to their values: we don't need sliding windows anymore! We use sliding ubuntu! Then, we greedily consider each rock in the order of their values, if we can jump furtherer, we jump. This solution is simpler and looks elegant to me.
- There are other solutions uses BIT or sets, make acceptable
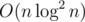 solutions.
solutions.
Problem D. Dice Rolling
Tricky case-study problem. Define the opposite faces as a "set". The key to this problem is the following lemma:
Lemma: Let {l, r} be a "set". In any dice rolling sequence, between two occurrence of l there must exist an r.
So, let the sum be the sum of two numbers in a "set", the answer must be a multiple of sum plus some remaining extra (at most three) larger number in some sets. So the special cases started by studying n = 1 or m = 1, then n = 2 or m = 2, then n ≥ 3 and m ≥ 3. The very special case is when (n, m) = (2, 4) or (4, 2).
Problem E. Escaped String
At first glance, it seems to be a classical O(n2) dynamic programming: dp[i][j] is defined to be the shortest possible length of subsequence s of A[0..i] and the first occurrence in string B as a subsequence ending at j-th character. Then we have the following:
- dp[i][j] = dp[i - 1][j], if A[i] ≠ B[j].
- dp[i][j] = min{dp[i - 1][j], dp[i - 1][prevB(j - 1, A[i - 1])]}, if A[i] = B[j], where prevB(j - 1, A[i - 1]) is the previous occurrence of A[i - 1] appear in string B before index j - 1.
However, this needs an O(n2) size memory, which is unaffordable. By observing that the dynamic programming state is meaningful only when A[i] = B[j], we can use a memory efficient encoding for storing these DP states. Please refer to My code for implementation.
The second solution is to notice that the answer is always less or equal to 1 + the maximum occurrence of any single letter (i.e., ≤ 501). This is because one can greedily choose the character α such that the index that the "next α" occurring in A ≤ the index of the "next α" occurring in B, among these character we choose the largest indexed α in B. It gives us a solution of length no more than 501. Now, we can use the LIS idea: let 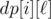 to be the largest index j in B such that there exists a subsequence of A[0..i] of length
to be the largest index j in B such that there exists a subsequence of A[0..i] of length 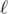 occurs in B[0..j] (or set j = n if this sequence is not a subsequence of B) but not B[0..j - 1].
occurs in B[0..j] (or set j = n if this sequence is not a subsequence of B) but not B[0..j - 1].
Then the recurrence relation is: 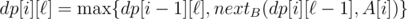 .
.










Auto comment: topic has been updated by tmt514 (previous revision, new revision, compare).
I'm able to understand the first solution of E, but was stuck on the second one: I'm feeling that the operator should be min rather than max.
If I got it right, that indicates the subsequence ends with b[j], causing every larger possible index j' > j not to satisfy the condition "... not in B[0... j' - 1]". Therefore the DP value dp[i][l] is the smallest length of a prefix of B containing a subsequence of A[0... i] with length l. In this way the DP values should be calculated by min. Perhaps I misunderstood the meaning of DP states?
And could you please explain in greater details how we can obtain the answer with the DP values described in this solution? Thanks in advance for help.
Ah, sorry, the description is not complete. Please refer to the description below:
Imagine that we have a lot of different subsequences of A[0..i] of length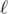 . For each subsequence x it corresponding to a index j such that x appears in B[0..j] (or j = n if there x does not appear in B at all) but not in B[0..j - 1]. In the case to find a "shortest possible solution", we want to make sure j is as large as possible.
. For each subsequence x it corresponding to a index j such that x appears in B[0..j] (or j = n if there x does not appear in B at all) but not in B[0..j - 1]. In the case to find a "shortest possible solution", we want to make sure j is as large as possible.
Thanks! Now I'm able to understand the recurrence.
BTW can I take a peek at test #53? I got RE #10 on first submission and RE #53 after doubling the array sizes, and I'm still unable to figure out what's wrong after doing stress tests myself.
It's here: https://gist.github.com/tmt514/8d999a907e334a58b2e7fc6ab0ecdcfa
Turns out that I defined the length of the answer string as signed char... (/_ ) Finally passed all tests, thanks for the help and patience!
Auto comment: topic has been updated by tmt514 (previous revision, new revision, compare).
Could you please elaborate on how to solve B?
Because getting the number of 1's linearly for every number from [0, b] does not seem the way to do it. Neither using the function __builtin_popcount. I tried to compute the number of ones from some 2**x to 2**y by using binomial coefficients, and then reduce the range to [a, b] but I believe this is again the wrong way.
Thanks,
Hi,
The key is to focus on only the i-th bit of each integer. (And we sum up for every i.) For example, if we look at the binary digit corresponds to 22 in the range [17, 25], we have: 0, 0, 0, 1, 1, 1, 1, 0, 0. The total number of 1-bits are: count2(25) - count2(17), which is 12 - 8 = 4.