Tobby_And_Friends's blog

Help on a combinatorics problem (UVA 10883)
By Tobby_And_Friends, history, 8 years ago, In English

Link: https://uva.onlinejudge.org/external/108/10883.pdf

I could figure out that let's say for 5 numbers the answer is (Arr[1] + 4 * Arr[2] + 6 * Arr[3] + 4 * Arr[4] + Arr[5])/2^16. So the problem basically reduces to finding the values in the nth row of pascal's triangle and power of 2. But I am not very sure as to how to implement the solution. Any help is really appreciated.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

HINT: If you calculate in the paper, you will see answer is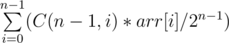

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can use the fact that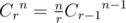 , i.e. no need of pre-computation. You can find a similar problem here

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yeah, recursively like C(n,  k)  =  C(n,  k  -  1)  *  (n  -  k  -  1)  /  k

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

HINT 2: Number of combinations can calculated recursively: C(n, k) = C(n, k - 1) * (n - k - 1) / k

Also C(n, 0) = 1

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

HINT 3: For bigger n finding combination will not be work, so use logarithm : )

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If you couldn't solve, see solution with logarithm and numerical combinations

→ Reply