Tobby_And_Friends's blog

Number Theory Problem from UVA (UVA 11774 — Doom’s Day)
By Tobby_And_Friends, history, 8 years ago, In English

Link: https://uva.onlinejudge.org/external/117/11774.pdf

I understand that the for n == m answer is 2. But I can't figure out the solution when n != m. I mean I basically do not understand the theory behind the solution (apart from trying out for small test cases). Any help is really appreciated.

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Let's decrease all numbers by 1 as real programmers do :).

Now we can observe that if we had a number x on some place then after one permutation we have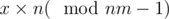 . Now we just want to know what is the minimum power of n which gives 1 modulo nm - 1.

A similar problem but harder: Problem B

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If it is not too much of a trouble can you please elaborate a bit? I could not understand to be honest. :( :'(

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Look at the first picture 9*3. We see that 3 becomes 1 (I calculate with 1 decreased from every number — actually it's 4 becomes 2). Now let's see that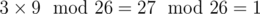 . The same could be observed for every other number except the one in the right bottom.

      Now let's take 1. We want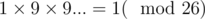 for some number of multiplications. That's what I meant saying about lowest power of n.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Observe grid when n=m. In this case answer is always 2. If n!=m if you look some cases you will see answer is n+m. Good luck :)

→ Reply