| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3831 |
| 3 | Radewoosh | 3646 |
| 4 | jqdai0815 | 3620 |
| 4 | Benq | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | gamegame | 3386 |
| 10 | ksun48 | 3373 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 164 |
| 1 | maomao90 | 164 |
| 3 | Um_nik | 163 |
| 4 | atcoder_official | 160 |
| 5 | -is-this-fft- | 158 |
| 6 | awoo | 157 |
| 7 | adamant | 156 |
| 8 | TheScrasse | 154 |
| 8 | nor | 154 |
| 10 | Dominater069 | 153 |
Given an integer n you need to calculate the number of distinct permutations {1, 2, 3, ..., n} such that the permutation represents a linear max heap.
In other words for each position from 1 to n: p[i] > p[2*i] and p[i] > p[2*i+1]
Example: Input: 4 Output: 3
I need help solving this problem, at least a hint please.
Here
Is the runtime O(N) (assume we have preprocessed factorial and modular inverse of factorial) .
No, it's O(NlogN), because the modular inverse is calculated in O(log), atleast I don't know how to do it faster :)
If you know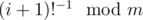
, you can find out 
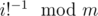in O(1). 
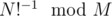can be computed in O(n).
Ohh yeah I just noticed it now
(n!) - 1 = (n + 1) * ((n + 1)!) - 1
Is this correct ?
Yes, that's the recurrence. Another way to do it, using one more array, is to precompute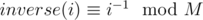
for every i in 
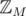, then 
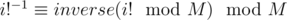. Here are some ideas to compute inverse efficiently.
I don't think it would be possible to precompute for all i because M can be very large (109 + 7)
In that problem M is 666013.
Yeah you are right . The preprocessing part takes O(NlogN) , and the part to calculate the number of heaps till N can be done in O(N) using the recurrence that you've posted . So overall it's O(NlogN) .
Thanks!