Приветствую всех участников раунда!
215A - Цепная передача
Из-за совсем небольших ограничений мы переберем i от 1 до n, переберем j от 1 до m, проверим, что bj делит ai нацело без остатка и среди всех таким пар найдем максимальное значение величины 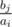 . Затем запустим этот алгоритм еще раз, таким образом найдем искомое количество пар, где достигается максимальное значение.
. Затем запустим этот алгоритм еще раз, таким образом найдем искомое количество пар, где достигается максимальное значение.
215B - Олимпийская медаль
Пусть нам известны выбранные значения r1, p1 и p2. Запишем равенство:
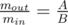
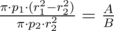
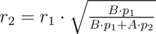
Нетрудно заметить, что для того, чтобы максимизировать величину r2 необходимо взять r1 и p1 — максимальными, а p2 — минимальным среди предоставленных значений. Простой перебор тремя циклами всевозможных значений не проходил из-за ограничения по времени, однако допустимо было заметить зависимость хотя бы для одной величины, а две другие перебирать.
215C - Крестики
Переберем величины n1 = max(a, c) и m1 = max(b, d) — размеры ограничивающего прямоугольника. Далее нам надо найти значение величины f(n1, m1, s), а к ответу прибавить f(n1, m1, s)·(n - n1 + 1)·(m - m1 + 1), где последние две скобки дают количество способов расположить ограничивающий прямоугольник в данном клетчатом поле.
Теперь нам надо подсчитать величину f(n1, m1, s). Ну во-первых, если n1·m1 = s, то ответ функции равен 2·(⌊ n1 / 2⌋ + 1)·(⌊ m1 / 2⌋ + 1) - 1 (попробуйте сами догадаться почему).
Если же n1·m1 > s, то нам надо выкинуть 4 уголка, которые являются одинаковыми прямоугольниками площадью 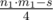 . Мы можем перебрать одну из сторон уголка, найти вторую, проверить что все ограничения выполняются, и за каждую найденную пару сторон прибавить к ответу функции по 2.
. Мы можем перебрать одну из сторон уголка, найти вторую, проверить что все ограничения выполняются, и за каждую найденную пару сторон прибавить к ответу функции по 2.
Таким образом, решение работает за O(n3), однако, с очень маленькой константой гораздо меньшей, чем 1.
215D - Жара
В этой задаче достаточно было понять, что задачу можно независимо решать по областям, и что возможно только одна из двух ситуаций при решении для каждой области: мы всех школьников рассаживаем в один автобус или берем минимальное количество автобусов так, чтобы никто из них не потребовал компенсации. То есть никогда не выгодно, чтобы часть школьников сидела в жарком автобусе, а часть – в холодном.
Достаточно подсчитать эти величины и взять минимум.
215E - Периодические числа
Скоро появится…











Имеется ввиду садим в 1 автобус?
а почему так?
Тех к сидит в жарких, можно посадить в один жаркий, тогда не нужно будет оплачивать лишние автобусы.
а почему невыгодно посадить часть в 1 жаркий, а другую часть в несколько холодных?
Я решал формулой, там получалась линейная функция относительно переменной, поэтому надо было брать либо 1 автобус, либо К автобусов так, чтобы все сидели в холодных.(Зависит от знака коэффициента при переменной)
Потому что когда мы разделяем одну группу на несколько для того что бы кто то перестал сидеть в жаре то мы или строго увеличиваем стоимость или уменьшаем.
понял, спасибо!
Какие решения ещё были по C? Может было проще что? А то я что то пока не понимаю формул в разборе.
вы можете задать интересующий вас вопрос, я поясню
Спасибо, уже разобрался.
Так, это сообщение было в другую тему.
По разбору тоже скажу — спасибо, все ясно. D была очень простой, а я, вместо того, чтобы подумать, написал дурацкий тернарник и дебажил его больше полутора часа, обидно :\
В раунде не участвовал, под конец просто открыл почитать задачки. Сразу открыл Б.... и задумался минут на 20. После 20 минут придумал что-то типа того, что в разборе, но потом перечитал условие, увидел см^3 и закрыл задачу нафиг....
У меня в Е была такая штука: Будем перебирать длину числа(в битах) и длину периода, а потом говорить сколько из них меньше заданного Н. Бинарным поиском найдем самую большую основу периода заданной длины, чтобы потом когда ее многократно склеить получить число не большее Н. Любой период меньше заданного нам подходит, поэтому добавим их к ответу, но нас интересуют только нецикличиские периоды, поскольку, меньшие мы уже посчитали. Количество нециклических периодов = все периоды минус цикличиские, то есть все делаем рекурсивно. Прим.: здесь "больший период" тот, который больше, как число, а не по длине:)
Можете по-подробнее D-шку объяснить?
Допустим, возьмем один автобус и посадим туда всех школьников. Тогда посмотрим на величины (Ti - ti)·xi и costi. Если первая меньше и температура больше критической, то выгодно выделить дополнительный автобус, причем, выделить столько автобусов, чтобы температура внутри стала меньше критической. А если вторая величина меньше, то вообще выделять дополнительные автобусы не выгодно.
Таким образом мы берем либо один автобус, либо столько, чтобы температура внутри стала ≤ Ti.
А почему цена, которая будет заплачена, если все сидят в одном или все рассажены по нежарким автобусам, будет меньше, чем если K человек сидит в жарком и n-k рассажены по нежарким?
up: все, сам разобрался. ****
0) при рассадке по дополнительным автобусам, очевидно, надо сажать по T-t человек. Если t=>T, то все едут в одном автобусе и ответом будет cost+n*x
1) если все будут сидеть в жарком автобусе, то будет потрачено n*x+cost (если все сидят в одном автобусе и он холодный, то ответом, очевидно, будет cost)
2) если k человек будут сидеть в холодных автобусах, n-k в жарком (одном автобусе, т.к. если есть несколько жарких,то надо сделать один жаркий), будет потрачено (k/(T-t))*cost + (n-k)*x + cost Теперь сравним потраченную сумму в случае 1) и в случае 2):
Сумма 2)- сумма 1)=dif= (k/(T-t))*cost + (n-k)*x + cost — n*x — cost= (k/(T-t))*cost -k*x= k*(cost/(T-t)-x )=k*(cost-x*T+x*t)/(T-t). dif <0 при cost-x*T+x*t <0 (предполагаем, что T-t>0- иначе см. пункт 0 ) т.е cost<x*(T-t). а это значит, что автобус стоит дороже, чем сумма всех неустоек его пассажиров, но, тогда этих пассажиров не надо рассаживать. Т.е. dif>=0 , т.е. сумма1)<=сумма2).
Аналогично доказывается, что сумма2)>= суммы в случае, если все рассажены по холодным автобусам
215D - Жара
Arcady27, мне не очевидно. Объясните, пожалуйста.
Потому что если посадить меньше чем T-t, то останется лишнее место, а если посадить больше чем T-t, то тогда не будет смысла этого делать, т.к. мы заплатим и неустойку, и за лишний автобус. Таким образом температура в автобусе будет на пределе.
Спасибо.
Это максимальное число учеников, которых можно посадить в один автобус так, чтобы они не просили неустойку, то есть
(T — t) + t не превышает T, но если посадить еще одного ученика, то они будут просить неустойку.
Спасибо.
Можно для дураков, как из второго предложения следует третье? У меня получается наоборот.
Блиин такая обида... D — шку оказывается правильно написал, и все случаи точно так же разобрал. Единственное — long long не поставил. Вот и 8 протест не проходил.
"протест", а не "претест" — прикольная опечатка:)
Бррр гоню))) вот что значить коментить посреди ночи)
А оказывается не очень и сложно)))
Why in problem D (Hot Days) you only need to consider the two situations mentioned? Thank you.
because the cost is a linear function about the number of buses
I also can't understand the solution
Supose that we will arrange n buses in ith city: If T[i]-t[i]>m/n , no children will get compensations.
If T[i]-t[i]<k/n , ans=cost[i]*n+{m-(T[i]-t[i])*(n-1)}*x[i] =cost[i]*n+m*x[i]-(T[i]-t[i])*n*x[i]+(T[i]-t[i])*x[i] ={cost[i]-(T[i]-t[i])*x[i]}*n+(T[i]-t[i])*x[i]
cost[i],x[i],T[i],t[i],m is known,and it's a linear function about "n".So the MinCost must appear on the endpoints.
Thanks a lot. I get it now :)
Жду с нетерпением разбор Е. Сам сдал, но интересно, как это сделать проще.)
Задача С: при вычисление функции F в разборе вероятно допущена ошибка — площади прямоугольников ("уголков"), которые следует вычесть из площади ограничивающего прямоугольника, по формуле Spr = (s — n1 * m1) / 4 получится отрицательной, ведь на данном этапе рассматривается случай n1 * m1 > s.
спасибо, поправил
А когда появится разбор на задачу E? Очень хотелось бы узнать решение...
Уже есть неофициальный разбор.
если n1·m1 = s, то ответ функции равен 2·(⌊n1 / 2⌋ + 1)·(⌊m1 / 2⌋ + 1) - 1
Если s четное, ответ равен 0.Правильно?
да
I didnt get the solution for Crosses. Here f(n1,m1,s) denotes the number of crosses that can be created with area s and n1 = max(a,c) & m1 = max(b,d). But why are we adding f(n1,m1,s).(n-n1+1).(m-m1+1) to the answer ?
Because we can additionally position the center of the cross in (n - n1 + 1)·(m - m1 + 1) ways on the given grid.
So will you write the solution for the last problem too?
Why the solution to problem E still hasn't been published?
8 лет — недостаточно скоро?