Hello Everyone,
The problem set of the 2017 Hackatari Codeathon will be available in Codeforces Gym tomorrow, Monday Feb/13/2017 19:00.
You will have 9 problems and 5 hours to solve them. However, the problems' difficulty is similar to Div.2 contests, so you might only need half of that time to solve them.
The problem set was prepared by Hasan0540, linkinu, and Maram Tuffaha.
Thanks to RetiredAmrMahmoud and Pepe.Chess for testing the problem set.
Good luck!










Well I'll probably need more than half the time to solve some of them but thanks anyways for the contest. Will there be an editorial released afterwards?
Could someone give me some hints about problem B — 2Trees please?
Check on some random trees what are the depths of leaves merging in optimal answer.
Lets precalc two arrays for each of trees: leavesOdd and leavesEven (leaves of odd and even depths from the root of tree, it doesnt matter what to choose as a root).
Then you can notice that answer is always either 2 or 3.
2 can be achieved only when (leavesOdd0 = leavesOdd1 and leavesEven0 = leavesEven1) or (leavesOdd0 = leavesEven1 and leavesEven0 == leavesOdd1). It's because all the paths will be of the same parity and thus can be colored in 2 colors (color the first root into 1 and then layer by layer alterate color).
The other cases it's 3 because in any path which is of nonoptimal parity you can color leaf in the third color and connect it to path of whatever parity tou need.
Bro , we need editorial for this sweet contest :)
There will be an editorial available ?
Could someone give me some hint about problem F — Islands II and probelm H — Arcade, please?
4-dimensional dp for max amount of certain type of characters.
Let's calc dp[i][j][k][l] — max amount of '|' characters we can collect on our path from (0, 0) to (i, j) while having k '<' characters collected and l '-' characters collected. dp array should be initialized with negative infinite values. Transitions are dependant on character a[i][j]. So it's like:
1. (a[i][j] == '>')
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i - 1][j][k - 1][l], dp[i][j - 1][k - 1][l])
2. (a[i][j] == '-')
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i - 1][j][k][l - 1], dp[i][j - 1][k][l - 1])
3. (a[i][j] == '|')
dp[i][j][k][l] = max(dp[i][j][k][l], dp[i - 1][j][k][l] + 1, dp[i][j - 1][k][l] + 1)
The answer is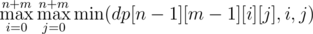
And you also need to optimize it from O(N4) memory to O(N3). Just store only previous and current layers of dp.
How to solve question F?