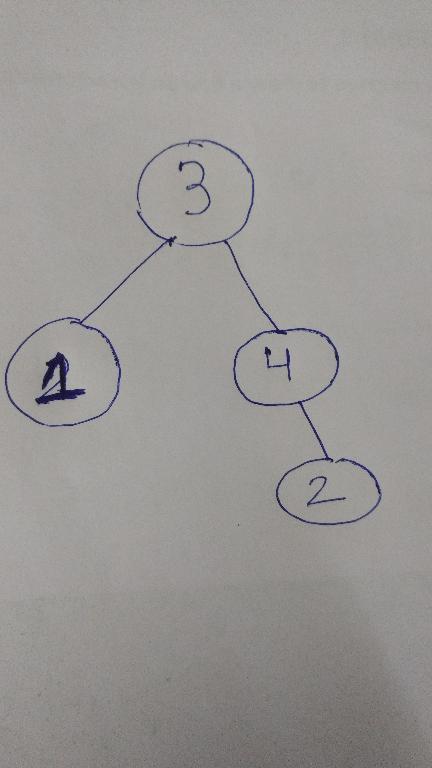
I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
- Number of Vertices :4
- Starting time ST[i]:2 4 1 3
- Ending time FT[i]:2 4 4 4
The Tree Looks Like:
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 4039 |
| 2 | tourist | 3841 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3590 |
| 5 | ecnerwala | 3542 |
| 6 | Benq | 3535 |
| 7 | orzdevinwang | 3526 |
| 8 | gamegame | 3477 |
| 9 | heuristica | 3357 |
| 10 | Radewoosh | 3355 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | atcoder_official | 160 |
| 3 | Um_nik | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
The Tree Looks Like:

| Name |
|---|



There exists a unique tree for each VALID start and end time arrays.
A small hint for the tree construction : The direct parent of a node i shall be a node j with maximum start time, following the constraint that start[j] < start[i] and end[j] ≥ end[i].
There exists such a node j for each node i, except the root.
A node having s_t == f_t must be leaf node. First insert the node having s_t == 1 into the tree and set pos(a variable) equal to this node. This "pos" will tell u the the position where to append the next_node into the tree. Along with it maintain a parent array. After appending a node(say i) at pos, check if s_t[i] == f_t[i], If yes then backtrack to the parent until u find a parent having f_t greater than the s_t of node i. This will become the new pos pointer. And if "no" then pos will be set to i for next node.In this way u can insert all nodes.