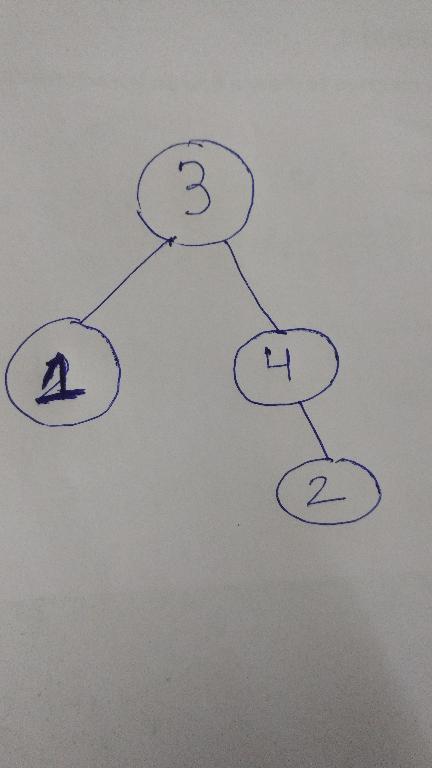
I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
- Number of Vertices :4
- Starting time ST[i]:2 4 1 3
- Ending time FT[i]:2 4 4 4
The Tree Looks Like:
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 4039 |
| 2 | tourist | 3841 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3590 |
| 5 | ecnerwala | 3542 |
| 6 | Benq | 3535 |
| 7 | orzdevinwang | 3526 |
| 8 | gamegame | 3477 |
| 9 | heuristica | 3357 |
| 10 | Radewoosh | 3355 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | atcoder_official | 160 |
| 3 | Um_nik | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
I'm interested in whether we can Construct a tree if we know the Starting Time and Ending Time of all the Vertices.
For Example:
The Tree Looks Like:

Hello everyone,
I was working on a problem where i was given an integer p and was asked to calculate the number of digits after the decimal point in 1/p.
Ex:- Input: 100 Output: 2 as (1/100=0.01)
#include<bits/stdc++.h>
using namespace std;
int main()
{
float p;
cin>>p;
float q=1/p;
int cnt=0;
cout<<q<<"\n";
while(fmod(q,10.0)!=0)
{
q=q*10;
cnt++;
//cout<<q<<" "<<cnt<<"\n";
}
cout<<cnt-1<<"\n";
}
What i was trying to do is multiply (1/n) till it is divisible 10 and then simply print count-1 .
But the output this code is giving me is 12 in place of 2 for p=100.
Help would be appreciated :)
| Name |
|---|


