let there be 3 integers x, y, z
their multiplication (x * y * z) is can be calculated either as (x * y) * z or x * (y * z) // associativity holds
now assume x / (y * z) = x * (1 / y) * (1 / z)
let Y and Z be the multiplicative modular inverse of (1 / y) and (1 / z) respectively
then result can be written as x * Y * Z
here (x * Y) * Z != x * (Y * Z) { WHY ? } // associativity does not holds
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:45:47
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
31:45:47
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 09:49:14 (j3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Why do you think associativity does not hold on the last line? It does.
For example, let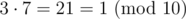 ) and
) and 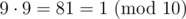 ). After you have the values which you are going to multiply, the order does not matter again:
). After you have the values which you are going to multiply, the order does not matter again: 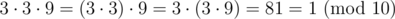 .
.
x = 3,y = 7, andz = 9, and let the modulo be10. We haveY = 3(sinceZ = 9(sinceNow, if you have different results with different orders, it probably means you have an error elsewhere. For example, you may be trying to multiply integers of order 109 in an
int32type, which is wrong since the result can of the order 1018.Gassa Sir, thanks for reply, but I am still confused.
I was refering to this question on codechef.
here is the accepted solution link.
here is the wrong one link.
only difference in the above submissions is different association while calculating answer.
I am pretty sure that i am taking care of overflow.
Where am I wrong then ?
In the second one, the expression is essentially
res += (A * (B * C) % M) % M;which is evaluated as
res += ((A * (B * C)) % M) % M;See, since
*and%have the same priority, it goes as follows: first calculatetemp = B * C, then multiplyAbytemp(here is the overflow), and only then take the result moduloM. Perhaps you meantres += (A * ((B * C) % M)) % M;The
(B * C)parens don't matter for the compiler, but(B * C % M)do.Thanks.
That was very silly on my part.
It would have cost me lots of wrong submissions in future.