The USACO US Open contest for the 2016-2017 season is going to run from 3/10 to 3/13. Let's discuss the contest and the problems here after the contest :)
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:10:36
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
25:10:36
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/22/2024 16:24:25 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Participation link please?
I think the contest will held in usaco.org according to clist.by
UPD: Yes, I was true.
The contests is running.
The input/output file name of problem Switch Grass in Platinum division is incorrect. It should be "grass.in/.out".
Is the second test case of problem 1 pelatinum correct?!
UPD: it's correct
The contest isn't over yet.
Common...!!!
One test of the first problem which mey be wrong!!!
I doubt that their test cases are wrong, but if they are, you should just email them.
What's the Email?
[email protected]
I had the same wrong test,which is test 2.I think there is something we do not considered.
I think the test case is correct. I know people that have gotten it.
It's definitely correct. My AC solution passed it.
So hard contest... How to solve SWITCH GRASS from platinum?
I think there is still 1 hour in the contest. Edit: When I started the contest, I checked the latest time you could start the contest, and it was four hours ago.
clist
Unlike last time, this contest was 5 hours instead of 4 (clist didn't take this into account).
Didn't get it in contest but I think this should work: sort the edges in increasing order of their weights and suppose at some point of time edge u-v is the lightest active edge. This means that for all edges which are lighter than this edge, the id's of their vertices are equal. Now the key observation is that in most of the cases this implies the id's of u and v are equal too. So you only need to consider the "important" edges- i.e. add the edges one by one in increasing order of weight, and reject edge u-v if u and v are already in the same connected component. Notice that is basically Kruskal's algorithm for finding a minimum spanning tree, so it suffices to solve the problem on a tree. This should be easy by keeping a bunch of multisets for each node.
Can you please explain how you will solve the problem for a tree using multisets?
Here's my implementation (gets AC): code. For each vertex I maintain a map of multisets which store for each color the list of its children with that color and an additional multiset which stores the weights of the optimal children of each color. Details should be clear from the code.
You can still start the contest on the website, so discussion should probably not happen yet.
How to solve Platinum 2?
I wrote an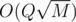 solution which passed just 3 test (the same as the stupid one with checking the all adjacent vertices). The basic idea is to divide the updates in sqrtM equal parts .Did someone do that and if so
solution which passed just 3 test (the same as the stupid one with checking the all adjacent vertices). The basic idea is to divide the updates in sqrtM equal parts .Did someone do that and if so
Notice that in any cycle of the graph, if there are at least two types of grass, then there are at least two edges that connect different types of grass. Therefore, the largest edge in any cycle will never be used as the answer, so it can be removed. This is equivalent to reducing the graph to its minimum spanning tree. The rest is just lazy propagation to update the children of the node changed in each update.
How does the lazy propagation work?
Let each node store the distance to its parent. Order these values such that for each node, all its children (and only its children) exist as a subarray, and that all children with the same grass type are also consecutive. Build a segment tree on this array. Now when we update node I from A to B, we make invalid all its children with type B (add infinity to all these nodes), and similarly make valid all children with type A (subtract infinity from these nodes). This is a range update, so we use lazy propagation. We should change the validity of node I as well, depending on the grass type of its parent. To get the answer, just query for the minimum value in the entire range. There are some annoying details to take care of, such as how changing the grass types of the nodes changes their ordering, but it can be done.
I also saw this in-contest, but couldn't figure out how to change the ordering of the children if one of their grass types changed. Can you elaborate on this section?
Simply leave extra spaces in the array to move nodes around. Before building the array, read the queries and calculate where the extra spaces are needed.
Cool! thanks :)
Are you sure about your complexity? My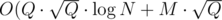 (~ 10^9 operations) passed 7 cases out of 10.
(~ 10^9 operations) passed 7 cases out of 10.
Oh actually its something like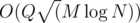 but I still don't think it should have TLEd on everything. Probably it TLEd because of a big constant. Thanks for the response. At least now I know that I probably got the idea for the solution.
but I still don't think it should have TLEd on everything. Probably it TLEd because of a big constant. Thanks for the response. At least now I know that I probably got the idea for the solution.
It can actually be solved in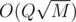 , but the solution has many little complications to avoid the log factor. One of the cooler things I to avoid using set is buckets to create a structure which provides insertion and deletion of elements in O(1) and minimum query in
, but the solution has many little complications to avoid the log factor. One of the cooler things I to avoid using set is buckets to create a structure which provides insertion and deletion of elements in O(1) and minimum query in 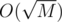 which is fine since you have only Q queries for minimum. However, I haven't submitted it, does anyone know when will the problems be available for upsolving?
which is fine since you have only Q queries for minimum. However, I haven't submitted it, does anyone know when will the problems be available for upsolving?
It's actually one of the most beautiful problems I've seen :D
That's weird. I think you should solve more beautiful problems.
How do you solve it?
I agree lol. Did you solve it in contest? How did you do on the other problems?
So how do you solve it?
bad matrix multiplication
Anyone have something faster than O(100 ^ 4 * lg(100000)) in platinum P3? Such solution should pass (as it's hard to make constant factor large. I think it will go down as low as /16 ~ /50) but I wonder if there is any solution with better asymptotics.
My guess (which could be completely wrong) was that there is no faster solution aside from improvements in matrix multiplication. This problem seems to be equivalent, in some sense, to multiplying and exponentiating matrices.
Technically you can go down to something like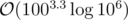 because matrix multiplication can be optimized.
because matrix multiplication can be optimized.
Is there faster solution for P2? Faster than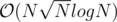 ?
?
UPD: Oh! I find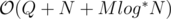 solution! :)
solution! :)
I only got 9/16 test cases on platinum #3 because I forgot to run the variable-mapping procedure parallely at one place :((( Couldve gotten a full score on that and a nonzero chance at camp with a simple 2 line fix :(((
Does anyone have any idea when the results will be released?
http://www.usaco.org/index.php?page=open17results
usaco gold problem 2:" we unfortunately had to revoke this problem since an algorithmic flaw was identified that invalidates the solution approach we had in mind -- making the problem far harder than intended" But Why? isnt it far harder? why not giving its score for those who solved it and spend a lot of time on it ?
By "far harder", we mean NP-complete. So it would be extraordinary if you did actually solve it.
I did solve this problem and got all 10 test cases. Actually this took up the bulk of my time, as I didn't have enough time to do the last problem. So I got 633. My argument is that the problem shouldn't be thrown out if it is indeed solvable, and if it had been factored in, then the cutoffs would have been far lower, and I would have possibly qualified.
The problem, as it was stated, was impossible to solve with the given constraints (unless P=NP). The judge solution was incorrect because it was finding a longest path in a DAG, whereas the nature of the graph meant it could have had cycles, in which finding longest path is NP complete.