Перед вами разбор задач сегодняшнего контеста. Я постарался расписать решения задач как можно более подробно, но если что-то будет непонятно, смело пишите в комментариях! :)
404 Not Found
#include <iostream>
#include <map>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
map<string, int> vals;
vals["Tetrahedron"] = 4;
vals["Cube"] = 6;
vals["Octahedron"] = 8;
vals["Dodecahedron"] = 12;
vals["Icosahedron"] = 20;
int n; cin >> n;
int res = 0;
for (int i = 0; i < n; i++) {
string s; cin >> s;
res += vals[s];
}
cout << res << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class PolyhedronSums {
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
HashMap<String, Integer> vals = new HashMap<String, Integer>();
vals.put("Tetrahedron", 4);
vals.put("Cube", 6);
vals.put("Octahedron", 8);
vals.put("Dodecahedron", 12);
vals.put("Icosahedron", 20);
int n = Integer.parseInt(reader.readLine());
int res = 0;
for (int i = 0; i < n; i++) {
res += vals.get(reader.readLine());
}
writer.write(Integer.toString(res));
reader.close();
writer.close();
}
}
vals = {
'Tetrahedron': 4,
'Cube': 6,
'Octahedron': 8,
'Dodecahedron': 12,
'Icosahedron': 20
}
n = int(input())
ans = 0
for i in range(0, n):
ans += vals[input()]
print(ans)
Подумайте, какие отрезки выгодно брать, если Антон сначала занимается шахматами, потом программированием, и наоборот.
#include <iostream>
#include <algorithm>
const int infinity = 1234567890;
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int n; cin >> n;
vector<pair<int, int> > a(n);
for (int i = 0; i < n; i++) {
cin >> a[i].first >> a[i].second;
}
int m; cin >> m;
vector<pair<int, int> > b(m);
for (int i = 0; i < m; i++) {
cin >> b[i].first >> b[i].second;
}
int minR1 = infinity, maxL1 = -infinity;
int minR2 = infinity, maxL2 = -infinity;
for (int i = 0; i < n; i++) {
maxL1 = max(maxL1, a[i].first);
minR1 = min(minR1, a[i].second);
}
for (int i = 0; i < m; i++) {
maxL2 = max(maxL2, b[i].first);
minR2 = min(minR2, b[i].second);
}
int res = max(maxL2 - minR1, maxL1 - minR2);
cout << max(res, 0) << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class TwoSegments {
public static final int infinity = 1234567890;
public static class Segment {
public int l;
public int r;
public Segment(int aL, int aR) {
l = aL;
r = aR;
}
}
private static Segment[] readList(BufferedReader reader) throws Exception {
int n = Integer.parseInt(reader.readLine());
Segment[] res = new Segment[n];
for (int i = 0; i < n; i++) {
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
int l = Integer.parseInt(tokenizer.nextToken());
int r = Integer.parseInt(tokenizer.nextToken());
res[i] = new Segment(l, r);
}
return res;
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
Segment[] a = readList(reader);
Segment[] b = readList(reader);
int minR1 = infinity, maxL1 = -infinity;
int minR2 = infinity, maxL2 = -infinity;
for (int i = 0; i < a.length; i++) {
maxL1 = Math.max(maxL1, a[i].l);
minR1 = Math.min(minR1, a[i].r);
}
for (int i = 0; i < b.length; i++) {
maxL2 = Math.max(maxL2, b[i].l);
minR2 = Math.min(minR2, b[i].r);
}
int res = Math.max(maxL2 - minR1, maxL1 - minR2);
writer.write(Integer.toString(Math.max(res, 0)));
reader.close();
writer.close();
}
}
infinity = 1234567890
minR1 = minR2 = infinity
maxL1 = maxL2 = -infinity
n = int(input())
for i in range(0, n):
(l, r) = map(int, input().split())
maxL1 = max(maxL1, l)
minR1 = min(minR1, r)
m = int(input())
for i in range(0, m):
(l, r) = map(int, input().split())
maxL2 = max(maxL2, l)
minR2 = min(minR2, r)
res = max(maxL2 - minR1, maxL1 - minR2);
print(max(res, 0))
В этой задаче были слабые претесты. Это было сделано для того, чтобы спровоцировать побольше взломов. И да, я предупреждал в анонсе :)
Промоделируйте процесс, чтобы узнать, как изменялось количество зерна в амбаре.
#include <iostream>
#include <cstdint>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
int64_t n, m;
cin >> n >> m;
if (n <= m) {
cout << n << endl;
} else {
n -= m;
int64_t l = 0, r = 2e9;
while (l < r) {
int64_t m = (l + r) / 2;
int64_t val = m * (m+1) / 2;
if (val >= n) {
r = m;
} else {
l = m+1;
}
}
cout << l + m << endl;
}
return 0;
}
import java.io.*;
import java.util.*;
public class SparrowsJava {
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
long n = Long.parseLong(tokenizer.nextToken());
long m = Long.parseLong(tokenizer.nextToken());
if (n <= m) {
writer.write(Long.toString(n));
} else {
n -= m;
long l = 0, r = (long)2e9;
while (l < r) {
long med = (l + r) / 2;
long val = med * (med+1) / 2;
if (val >= n) {
r = med;
} else {
l = med+1;
}
}
writer.write(Long.toString(l + m));
}
reader.close();
writer.close();
}
}
(n, m) = map(int, input().split())
if n <= m:
print(n)
else:
aM = m
n -= m
(l, r) = (0, int(2e9))
while l < r:
m = (l + r) // 2;
val = m * (m+1) // 2;
if val >= n:
r = m
else:
l = m+1
print(l + aM)
Решите упрощенную версию задачи. Пусть в нашей последлвательности сначала идет x открывающих скобок, потом y закрывающих скобок, притом последнюю открывающую скобку обязательно включать в ППСП. Используйте наивное решение, чтобы посмотреть, как будет выглядеть ответ. Подумайте, как действовать дальше.
#include <iostream>
#include <vector>
#include <cstdint>
using namespace std;
int mod = (int)1e9 + 7;
int64_t extGcd(int64_t a, int64_t b, int64_t& x, int64_t& y) {
if (!a) {
x = 0;
y = 1;
return b;
}
int64_t x1, y1;
int64_t d = extGcd(b % a, a, x1, y1);
x = y1 - (b / a) * x1;
y = x1;
return d;
}
inline int addMod(int a, int b, int m = mod) {
return ((int64_t)a + b) % m;
}
inline int mulMod(int a, int b, int m = mod) {
return ((int64_t)a * b) % m;
}
inline int divMod(int a, int b, int m = mod) {
int64_t x, y;
int64_t g = extGcd(b, m, x, y);
if (g != 1) {
cerr << "Bad gcd!" << endl;
for (;;);
}
x = (x % m + m) % m;
return mulMod(a, x, m);
}
const int factRange = 1000000;
int fact[factRange];
inline void precalcFactorials() {
fact[0] = 1;
for (int i = 1; i < factRange; i++) {
fact[i] = mulMod(fact[i-1], i);
}
}
inline int F(int n) {
return (n < 0) ? 0 : fact[n];
}
inline int C(int k, int n) {
return divMod(F(n), mulMod(F(n-k), F(k)));
}
int main() {
ios_base::sync_with_stdio(false);
string s;
cin >> s;
int len = s.size();
precalcFactorials();
vector<int> opnLeft(len), clsRight(len);
opnLeft[0] = (s[0] == '(') ? 1 : 0;
for (int i = 1; i < len; i++) {
opnLeft[i] = opnLeft[i-1] + ((s[i] == '(') ? 1 : 0);
}
clsRight[len-1] = (s[len-1] == ')') ? 1 : 0;
for (int i = len-2; i >= 0; i--) {
clsRight[i] = clsRight[i+1] + ((s[i] == ')') ? 1 : 0);
}
int res = 0;
for (int i = 0; i < len; i++) {
if (s[i] != '(' || clsRight[i] == 0) {
continue;
}
int add = C(opnLeft[i], opnLeft[i] + clsRight[i] - 1);
res = addMod(res, add);
}
cout << res << endl;
return 0;
}
import java.io.*;
import java.util.*;
public class BracketsJava {
public static int mod = (int)1e9 + 7;
public static class ExtGcdResult {
long x;
long y;
}
public static long extGcd(long a, long b, ExtGcdResult res) {
if (a == 0) {
res.x = 0L;
res.y = 1L;
return b;
}
ExtGcdResult newRes = new ExtGcdResult();
long d = extGcd(b % a, a, newRes);
res.x = newRes.y - (b / a) * newRes.x;
res.y = newRes.x;
return d;
}
public static final int addMod(int a, int b) {
return (int)(((long)a + b) % mod);
}
public static final int mulMod(int a, int b) {
return (int)(((long)a * b) % mod);
}
public static final int divMod(int a, int b) {
ExtGcdResult res = new ExtGcdResult();
long g = extGcd(b, mod, res);
if (g != 1) {
System.out.println("Bad gcd!");
for (;;);
}
int q = (int)((res.x % mod + mod) % mod);
return mulMod(a, q);
}
public static final int[] precalcFactorials() {
int[] fact = new int[factRange];
fact[0] = 1;
for (int i = 1; i < factRange; i++) {
fact[i] = mulMod(fact[i-1], i);
}
return fact;
}
public static final int factRange = 1000000;
public static final int[] fact = precalcFactorials();
public static final int F(int n) {
return (n < 0) ? 0 : fact[n];
}
public static final int C(int k, int n) {
int res = divMod(F(n), mulMod(F(n-k), F(k)));
return divMod(F(n), mulMod(F(n-k), F(k)));
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
String s = reader.readLine();
int len = s.length();
int[] opnLeft = new int[len], clsRight = new int[len];
opnLeft[0] = (s.charAt(0) == '(') ? 1 : 0;
for (int i = 1; i < len; i++) {
opnLeft[i] = opnLeft[i-1] + ((s.charAt(i) == '(') ? 1 : 0);
}
clsRight[len-1] = (s.charAt(len-1) == ')') ? 1 : 0;
for (int i = len-2; i >= 0; i--) {
clsRight[i] = clsRight[i+1] + ((s.charAt(i) == ')') ? 1 : 0);
}
int res = 0;
for (int i = 0; i < len; i++) {
if (s.charAt(i) != '(' || clsRight[i] == 0) {
continue;
}
int add = C(opnLeft[i], opnLeft[i] + clsRight[i] - 1);
res = addMod(res, add);
}
writer.write(Integer.toString(res));
reader.close();
writer.close();
}
}
Приношу извининения, что эта задача не была оригинальной. Я постараюсь, чтобы такое больше не повторилось.
Если у вас в этой задаче TL или ML, не стоит думать, что ограничения по времени/памяти слишком узкие. Авторское решение работает за 1.2 секунды и тратит 9 МБ памяти.
Разделите все запросы на 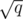 блоков. Затем разделите элементы на подвижные (те, которые будут изменяться в данном блоке) и неподвижные. Подумайте, как действовать дальше.
блоков. Затем разделите элементы на подвижные (те, которые будут изменяться в данном блоке) и неподвижные. Подумайте, как действовать дальше.
// Thanks to netman for the idea for this wonderful solution :)
#include <iostream>
#include <fstream>
#include <vector>
#include <cstdint>
#include <algorithm>
using namespace std;
class SQRTDecomposition {
private:
int n, sz;
vector<int> val;
vector<int> blocks;
public:
inline void add(int v, int delta) {
val[v] += delta;
blocks[v / sz] += delta;
}
inline int sum(int l, int r) {
if (l < 0) {
l = 0;
}
if (r >= n) {
r = n;
}
r++;
int res = 0;
int lBlock = (l + sz - 1) / sz, rBlock = r / sz;
for (int i = lBlock; i < rBlock; i++) {
res += blocks[i];
}
int lBlockR = lBlock * sz, rBlockR = rBlock * sz;
if (lBlockR >= rBlockR) {
for (int i = l; i < r; i++) {
res += val[i];
}
} else {
for (int i = l; i < lBlockR; i++) {
res += val[i];
}
for (int i = rBlockR; i < r; i++) {
res += val[i];
}
}
return res;
}
inline void clear() {
val.assign(val.size(), 0);
blocks.assign(blocks.size(), 0);
}
SQRTDecomposition(int n, int sz)
: n(n), sz(sz), val(n, 0), blocks((n + sz - 1) / sz, 0) {
}
};
struct ToProcess {
int x, y1, y2, sgn, id;
};
const int BLOCK_SZ_Q = 256;
const int BLOCK_SZ_N = 512;
const int MAX_N = 200000;
int n, q;
vector<ToProcess> sortedL[MAX_N], sortedR[MAX_N];
SQRTDecomposition sum(MAX_N, BLOCK_SZ_N);
int64_t ans[MAX_N], preAns[MAX_N];
pair<int, int> queries[MAX_N];
vector<int> goods;
int p[MAX_N];
bool good[MAX_N];
inline void add(int q, int sgn, int id) {
if (q-1 >= 0) {
sortedL[q-1].push_back({q-1, p[q]+1, n-1, sgn, id});
}
if (q+1 < n) {
sortedR[q+1].push_back({q+1, 0, p[q]-1, sgn, id});
}
}
int main() {
ios_base::sync_with_stdio(false);
cin >> n >> q;
for (int i = 0; i < n; i++) {
p[i] = i;
}
for (int i = 0; i < q; i++) {
cin >> queries[i].first >> queries[i].second;
queries[i].first--; queries[i].second--;
}
int64_t cnt = 0;
for (int i = 0; i < q; i += BLOCK_SZ_Q) {
int iEnd = min(q, i + BLOCK_SZ_Q);
for (int j = 0; j < n; j++) {
good[j] = false;
}
for (int j = i; j < iEnd; j++) {
good[queries[j].first] = true;
good[queries[j].second] = true;
}
goods.clear();
for (int j = 0; j < n; j++) {
if (good[j]) {
goods.push_back(j);
}
}
int64_t goodCnt = 0;
for (int j = 0; j < n; j++) {
sortedL[j].clear();
sortedR[j].clear();
}
for (int j = i; j < iEnd; j++) {
int a = queries[j].first, b = queries[j].second;
if (a == b) {
ans[j] += goodCnt;
continue;
}
for (int k = 0; k < (int)goods.size(); k++) {
int q = goods[k];
if (q == a || q == b) {
continue;
}
if ((p[q] < p[a] && q > a) ||
(p[q] > p[a] && q < a)) {
goodCnt--;
}
if ((p[q] < p[b] && q > b) ||
(p[q] > p[b] && q < b)) {
goodCnt--;
}
if ((p[q] < p[b] && q > a) ||
(p[q] > p[b] && q < a)) {
goodCnt++;
}
if ((p[q] < p[a] && q > b) ||
(p[q] > p[a] && q < b)) {
goodCnt++;
}
}
if ((a < b && p[a] > p[b]) ||
(a > b && p[a] < p[b])) {
goodCnt--;
} else {
goodCnt++;
}
ans[j] += goodCnt;
add(a, -1, j);
add(b, -1, j);
swap(p[a], p[b]);
add(a, +1, j);
add(b, +1, j);
}
sum.clear();
for (int j = 0; j < n; j++) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (int k = 0; k < (int)sortedL[j].size(); k++) {
ToProcess &cur = sortedL[j][k];
int64_t res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
sum.clear();
for (int j = n-1; j >= 0; j--) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (int k = 0; k < (int)sortedR[j].size(); k++) {
ToProcess &cur = sortedR[j][k];
int64_t res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
for (int j = i; j < iEnd; j++) {
if (j != i) {
preAns[j] += preAns[j-1];
}
ans[j] += cnt + preAns[j];
}
cnt = ans[iEnd - 1];
}
for (int i = 0; i < q; i++) {
cout << ans[i] << "\n";
}
return 0;
}
import java.io.*;
import java.util.*;
public class InversionNSqrtNNoVectors {
private static final int BLOCK_SZ_Q = 256;
private static final int BLOCK_SZ_N = 512;
public static class ToProcess {
public int x, y1, y2, sgn, id;
public void set(int pX, int pY1, int pY2, int pSgn, int pId) {
x = pX;
y1 = pY1;
y2 = pY2;
sgn = pSgn;
id = pId;
}
public ToProcess() {
}
}
public static class ToProcessCompareAsc implements Comparator<ToProcess> {
@Override
public int compare(ToProcess o1, ToProcess o2) {
return o1.x - o2.x;
}
}
public static class ToProcessCompareDesc implements Comparator<ToProcess> {
@Override
public int compare(ToProcess o1, ToProcess o2) {
return o2.x - o1.x;
}
}
static int n, q;
static int[] p;
static ToProcess[] queryL, queryR;
static int queryLCnt, queryRCnt;
static SQRTDecomposition sum;
static ToProcessCompareAsc ascCmp = new ToProcessCompareAsc();
static ToProcessCompareDesc descCmp = new ToProcessCompareDesc();
public static final void add(int q, int sgn, int id) {
if (q-1 >= 0) {
queryL[queryLCnt++].set(q-1, p[q]+1, n-1, sgn, id);
}
if (q+1 < n) {
queryR[queryRCnt++].set(q+1, 0, p[q]-1, sgn, id);
}
}
public static void main(String[] args) throws Exception {
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer tokenizer = new StringTokenizer(reader.readLine());
n = Integer.parseInt(tokenizer.nextToken());
q = Integer.parseInt(tokenizer.nextToken());
int[] qL = new int[q], qR = new int[q];
long[] ans = new long[q], preAns = new long[q];
p = new int[n];
for (int i = 0; i < n; i++) {
p[i] = i;
}
for (int i = 0; i < q; i++) {
tokenizer = new StringTokenizer(reader.readLine());
qL[i] = Integer.parseInt(tokenizer.nextToken()) - 1;
qR[i] = Integer.parseInt(tokenizer.nextToken()) - 1;
}
long cnt = 0;
boolean[] good = new boolean[n];
int[] goods = new int[n];
int goodsSize = 0;
queryL = new ToProcess[4 * BLOCK_SZ_Q]; queryR = new ToProcess[4 * BLOCK_SZ_Q];
for (int j = 0; j < 4 * BLOCK_SZ_Q; j++) {
queryL[j] = new ToProcess();
queryR[j] = new ToProcess();
}
SQRTDecomposition sum = new SQRTDecomposition(n, BLOCK_SZ_N);
for (int i = 0; i < q; i += BLOCK_SZ_Q) {
int iEnd = Math.min(q, i + BLOCK_SZ_Q);
Arrays.fill(good, false);
for (int j = i; j < iEnd; j++) {
good[qL[j]] = true;
good[qR[j]] = true;
}
goodsSize = 0;
for (int j = 0; j < n; j++) {
if (good[j]) {
goods[goodsSize++] = j;
}
}
long goodCnt = 0;
queryLCnt = 0;
queryRCnt = 0;
for (int j = i; j < iEnd; j++) {
int a = qL[j], b = qR[j];
if (a == b) {
ans[j] += goodCnt;
continue;
}
for (int k = 0; k < goodsSize; k++) {
int q = goods[k];
if (q == a || q == b) {
continue;
}
if ((p[q] < p[a] && q > a) ||
(p[q] > p[a] && q < a)) {
goodCnt--;
}
if ((p[q] < p[b] && q > b) ||
(p[q] > p[b] && q < b)) {
goodCnt--;
}
if ((p[q] < p[b] && q > a) ||
(p[q] > p[b] && q < a)) {
goodCnt++;
}
if ((p[q] < p[a] && q > b) ||
(p[q] > p[a] && q < b)) {
goodCnt++;
}
}
if ((a < b && p[a] > p[b]) ||
(a > b && p[a] < p[b])) {
goodCnt--;
} else {
goodCnt++;
}
ans[j] += goodCnt;
add(a, -1, j);
add(b, -1, j);
int tmp = p[a];
p[a] = p[b];
p[b] = tmp;
add(a, +1, j);
add(b, +1, j);
}
sum.clear();
Arrays.sort(queryL, 0, queryLCnt, ascCmp);
int curL = 0;
for (int j = 0; j < n; j++) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (; curL < queryLCnt; curL++) {
ToProcess cur = queryL[curL];
if (cur.x != j) {
break;
}
int res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
sum.clear();
Arrays.sort(queryR, 0, queryRCnt, descCmp);
int curR = 0;
for (int j = n-1; j >= 0; j--) {
if (!good[j]) {
sum.add(p[j], 1);
}
for (; curR < queryRCnt; curR++) {
ToProcess cur = queryR[curR];
if (cur.x != j) {
break;
}
int res = sum.sum(cur.y1, cur.y2);
res *= cur.sgn;
preAns[cur.id] += res;
}
}
for (int j = i; j < iEnd; j++) {
if (j != i) {
preAns[j] += preAns[j-1];
}
ans[j] += cnt + preAns[j];
}
cnt = ans[iEnd - 1];
}
for (int i = 0; i < q; i++) {
writer.write(Long.toString(ans[i]));
writer.newLine();
}
reader.close();
writer.close();
}
}
class SQRTDecomposition {
private int n;
private int sz;
private int[] val;
private int[] blocks;
public final void add(int v, int delta) {
val[v] += delta;
blocks[v / sz] += delta;
}
public final int sum(int l, int r) {
if (l < 0) {
l = 0;
}
if (r >= n) {
r = n;
}
r++;
int res = 0;
int lBlock = (l + sz - 1) / sz, rBlock = r / sz;
for (int i = lBlock; i < rBlock; i++) {
res += blocks[i];
}
int lBlockR = lBlock * sz, rBlockR = rBlock * sz;
if (lBlockR >= rBlockR) {
for (int i = l; i < r; i++) {
res += val[i];
}
} else {
for (int i = l; i < lBlockR; i++) {
res += val[i];
}
for (int i = rBlockR; i < r; i++) {
res += val[i];
}
}
return res;
}
public void clear() {
Arrays.fill(val, 0);
Arrays.fill(blocks, 0);
}
SQRTDecomposition(int pN, int pSz) {
n = pN;
sz = pSz;
val = new int[n];
blocks = new int[(n + sz - 1) / sz];
}
}
Альтернативное решение от Vladik:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <set>
#include <map>
#include <vector>
#include <iomanip>
#define sqr(a) (a)*(a)
#define all(a) (a).begin(), (a).end()
using namespace std;
template <typename T>
T next_int() {
T ans = 0, t = 1;
char ch;
do { ch = getchar(); } while(ch <= ' ') ;
if(ch == '-') {
t = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
ans = ans * 10 + (ch - '0');
ch = getchar();
}
return ans * t;
}
string next_token() {
char ch;
string ans = "";
do { ch = getchar(); } while(ch <= ' ') ;
while(ch >= ' ') {
ans += ch;
ch = getchar();
}
return ans;
}
const long long INF = (long long)1e18 + 227 + 1;
const int INFINT = (int)1e9 + 227 + 1;
const int MAXN = (int)2e5 + 227 + 1;
const int MOD = (int)1e9 + 7;
const long double EPS = 1e-9;
long long bin_pow(long long n, long long k) {
if(!k) return 1;
long long ans = bin_pow(n, k / 2);
ans = ans * ans % MOD;
if(k % 2) ans = ans * n % MOD;
return ans;
}
struct tree {
int size_block;
int len;
tree(int len) : len(len) {
size_block = sqrt(len);
kek.resize(len / size_block + 1, vector<int>(size_block, 0));
pr_block.resize(len / size_block + 1, 0);
}
vector<int> pr_block;
vector<vector<int> > kek;
void inc(int pos, int num) {
int x = pos / size_block;
for(int i = pos % size_block; i < size_block; i++) {
kek[x][i] += num;
}
for(int i = 0; i <= len / size_block; i++)
if(i == 0) {
pr_block[i] = kek[i][size_block - 1];
} else {
pr_block[i] = pr_block[i - 1] + kek[i][size_block - 1];
}
}
int f(int a) {
return a / size_block;
}
long long get(vector<int> &a, int l, int r, bool ok = 1) {
if(ok == 1) {
l %= size_block;
r %= size_block;
}
return a[r] - (l ? a[l - 1] : 0);
}
int get(int l, int r) {
if(l > r) return 0;
r = min(r, len);
if(f(l) == f(r))
return get(kek[f(l)], l, r);
int ans = 0;
if(l % size_block) {
ans += get(kek[f(l)], l, size_block - 1);
l += size_block - l % size_block;
}
if(r % size_block != size_block - 1) {
ans += get(kek[f(r)], 0, r);
r -= r % size_block + 1;
}
ans += get(pr_block, f(l), f(r), 0);
return ans;
}
int get_pref(int p) {
return get(1, p - 1);
}
int get_suff(int p) {
return get(p + 1, len);
}
} ;
struct mda {
vector<int> a;
vector<tree> t;
int len, sz;
long long ans;
mda(int len) : len(len) {
sz = 2000;
ans = 0;
a.resize(len + 1);
for(int i = 1; i <= len; i++)
a[i] = i;
for(int i = 1; i <= len; i += sz) {
t.push_back(tree(len));
for(int j = i; j < i + sz && j <= len; j++)
add(j, j);
}
}
int get_pref(int L, int R, int k) {
int ans = 0;
for(int l = 1; l <= R; l += sz) {
int r = l + sz - 1;
if(r < L || l > R) continue;
if(L <= l && r <= R)
ans += t[(l - 1) / sz].get_pref(k);
else
for(int i = max(l, L); i <= min(r, R); i++)
ans += (a[i] < k);
}
return ans;
}
int get_suff(int L, int R, int k) {
int ans = 0;
for(int l = 1; l <= R; l += sz) {
int r = l + sz - 1;
if(r < L || l > R) continue;
if(L <= l && r <= R)
ans += t[(l - 1) / sz].get_suff(k);
else
for(int i = max(l, L); i <= min(r, R); i++)
ans += (a[i] > k);
}
return ans;
}
void del(int p, int k) {
p = (p - 1) / sz;
t[p].inc(k, -1);
}
void add(int p, int k) {
p = (p - 1) / sz;
t[p].inc(k, 1);
}
void sw(int i, int j) {
if(i == j) return;
if(i > j) swap(i, j);
ans -= get_pref(i, j, a[i]);
ans -= get_suff(i, j, a[j]);
if(a[i] > a[j]) ans++;
del(i, a[i]);
del(j, a[j]);
swap(a[i], a[j]);
add(i, a[i]);
add(j, a[j]);
ans += get_pref(i, j, a[i]);
ans += get_suff(i, j, a[j]);
if(a[i] > a[j]) ans--;
}
} ;
int main() {
// freopen(".in", "r", stdin);
int n, m; cin >> n >> m;
mda t(n);
for(int i = 0; i < m; i++) {
int x, y; cin >> x >> y;
t.sw(x, y);
cout << t.ans << "\n";
}
}
Альтернативное решение от netman:
import java.io.*;
import java.util.*;
public class NsqrtNlogNnetman implements Runnable {
static class InputReader {
BufferedReader reader;
StringTokenizer tokenizer;
InputReader(InputStream in) {
reader = new BufferedReader(new InputStreamReader(in), 32768);
tokenizer = null;
}
String next() {
while (tokenizer == null || !tokenizer.hasMoreTokens()) {
try {
tokenizer = new StringTokenizer(reader.readLine());
} catch (IOException e) {
e.printStackTrace();
throw new RuntimeException(e);
}
}
return tokenizer.nextToken();
}
int nextInt() {
return Integer.parseInt(next());
}
long nextLong() {
return Long.parseLong(next());
}
double nextDouble() {
return Double.parseDouble(next());
}
}
static class Fenwick {
int[] ft;
Fenwick(int n) {
ft = new int[n];
}
void add(int r, int val) {
while (r < ft.length) {
ft[r] += val;
r |= r + 1;
}
}
int sum(int r) {
int res = 0;
while (r >= 0) {
res += ft[r];
r = (r & (r + 1)) - 1;
}
return res;
}
void clear() {
Arrays.fill(ft, 0);
}
}
static class Query {
int x, bound, sign, id;
Query(int x, int bound, int sign, int id) {
this.x = x;
this.bound = bound;
this.sign = sign;
this.id = id;
}
}
static void getOnPrefSmaller(List<Query> qrs, int r, int y, int id, int sign) {
qrs.add(new Query(r, y, sign, id));
}
static void getOnPrefBetween(List<Query> qrs, int r, int x, int y, int id, int sign) {
getOnPrefSmaller(qrs, r, y, id, sign);
getOnPrefSmaller(qrs, r, x, id, -sign);
}
static void getOnSegmentBetween(List<Query> qrs, int l, int r, int x, int y, int id, int sign) {
if (x > y) return;
getOnPrefBetween(qrs, r, x, y, id, sign);
getOnPrefBetween(qrs, l, x, y, id, -sign);
}
@Override
public void run() {
InputReader in = new InputReader(System.in);
PrintWriter out = new PrintWriter(System.out);
int n = in.nextInt();
int q = in.nextInt();
int[] l = new int[q];
int[] r = new int[q];
for (int i = 0; i < q; i++) {
l[i] = in.nextInt() - 1;
r[i] = in.nextInt() - 1;
}
int[] perm = new int[n];
for (int i = 0; i < n; i++) {
perm[i] = n - i - 1;
}
final int BLOCK = 300;
long inv = 0L;
boolean[] isInteresting = new boolean[n];
long[] add = new long[q];
Fenwick f = new Fenwick(n);
for (int i = 0; i < q; i += BLOCK) {
int from = i, to = Math.min(i + BLOCK, q) - 1;
List<Integer> lst = new ArrayList<>();
for (int j = from; j <= to; j++) {
lst.add(l[j]);
lst.add(r[j]);
}
lst.sort(Integer::compareTo);
lst = new ArrayList<>(new HashSet<>(lst));
int[] interestingPositions = lst.stream().mapToInt(x -> x).toArray();
for (int pos : interestingPositions) {
isInteresting[pos] = true;
}
List<Query> qrs = new ArrayList<>();
for (int j = from; j <= to; j++) {
if (l[j] == r[j]) continue;
if (l[j] > r[j]) {
int tmp = l[j];
l[j] = r[j];
r[j] = tmp;
}
if (perm[l[j]] < perm[r[j]]) {
getOnSegmentBetween(qrs, l[j], r[j], perm[l[j]], perm[r[j]], j,-1);
int leftValue = perm[l[j]];
int rightValue = perm[r[j]];
for (int pos : interestingPositions) {
if (pos > l[j] && pos < r[j] && perm[pos] > leftValue && perm[pos] < rightValue) {
add[j] -= 2;
}
}
add[j]--;
} else {
getOnSegmentBetween(qrs, l[j], r[j], perm[r[j]], perm[l[j]], j,1);
int leftValue = perm[l[j]];
int rightValue = perm[r[j]];
for (int pos : interestingPositions) {
if (pos > l[j] && pos < r[j] && perm[pos] > rightValue && perm[pos] < leftValue) {
add[j] += 2;
}
}
add[j]++;
}
int tmp = perm[l[j]];
perm[l[j]] = perm[r[j]];
perm[r[j]] = tmp;
}
qrs.sort(Comparator.comparingInt(a -> -a.x));
f.clear();
for (int pos = 0; pos < n; pos++) {
if (!isInteresting[pos]) {
f.add(perm[pos], 1);
}
while (!qrs.isEmpty() && qrs.get(qrs.size() - 1).x == pos) {
Query t = qrs.get(qrs.size() - 1);
qrs.remove(qrs.size() - 1);
add[t.id] += 2 * t.sign * f.sum(t.bound);
}
}
for (int j = from; j <= to; j++) {
inv += add[j];
out.println(inv);
}
for (int pos : interestingPositions) {
isInteresting[pos] = false;
}
}
out.close();
}
public static void main(String[] args) {
new Thread(null, new NsqrtNlogNnetman(), "1", 1L << 28).run();
}
}











Автокомментарий: текст был обновлен пользователем gepardo (предыдущая версия, новая версия, сравнить).
Auto comment: topic has been updated by gepardo (previous revision, new revision, compare).
Also notice that k can be found using a formula, but such solutions could fail by accuracy, because the formula is using the square root function.Is there any way to get the solution by formula either in c++ or python while still retaining accuracy?
use long double throughout
Can you tell why double gives error and not long double ?? I didn't get convincing proof about it.
it's because of how the IEEE 754 standard encodes floating point numbers. double is a 64-bit floating point type which means it has less than 64 bits for the mantissa (meaning it has less than 64 bits of precision; I think it has 53 bits of precision)
long double however is typically an 80-bit type which is AFAIK made specifically to have 64 bits for the actual data we care about.
even though the problem can be solved by this method, alternative methods that don't require fidgeting with extra precision floating point types are less likely to produce errors so I can't really recommend doing this always.
I did exactly that :)
25530268
Click
I thick you can get this ... solution
785A - Anton and Polyhedrons Hint: 404 Not Foundquit interesting:)Thanks! I like the way the editorial is written :D
Wow, Great Editorial. Equality of all languages.
Если в задаче C использовать long double (C++), то точности хватает. Тест на котором не хватает double: 999999998765257152 10 (ответ 1414213572)
long long is enough
25534855
This editorial with hints and opening blocks! Something new and beautiful in this edutorial! I've never senn something like this!
the iterative solution of C passes in time limit ... should've taken care about that..
It's hard to hack such solutions because of the following:
109 passes the time limit.
The constraints cannot be increased because 1018 is an almost maximal range for the constraints.
Test cases could have been added so that these kind of solutions get TLE. Anyways the contest was really good, so is the editorial. Thanks! :)
Do you really know the test that can cause these solutions to fail? As mentioned above, 10^9*(some really simple operations) fits the TL.
I was talking about multiple test cases in a single judge input file. One single test will always pass..
Or you can lowering the time limit :)
gepardo why you searched in 2*10^9 ? How you guess that for 10^18 1 ans will must between them ? What is the proof ?
If you see a formula given in the editorial and try k = 2·109, you'll see that it's quite enough to be the right binary search range.
It is also possible to solve C using linear search: 25518550
salute to alex256.. this is the best editorial i've ever seen..i've always wanted to have those "hints" kind of thing
Range tree + decard tree = O((n + q) * log n ^ 2) in problem E
Можешь объяснить свою идею?
Я пытался хранить в каждой вершине дерева отрезков декартово. При свапах я сначала удавляю элементы из соответстующих деревьев (пересчитывая инверсии в "соседних" вершинах ДО), а потом добавляю. O(n log n + q log^2 n). Но это не заходит по времени (я пытался запустить на кфе — оно на макстестах работает около 5.5 сек).
Рисуночек с объяснением и посылка
Мое решение за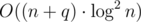 использовало похожую идею, только я хранил декартки не внутри ДО, а внутри дерева Фенвика.
использовало похожую идею, только я хранил декартки не внутри ДО, а внутри дерева Фенвика.
Еще одна идея, как соптимизировать решение и отказаться от декарток: давайте запомним, какие значения могли оказаться в каждой вершине дерева Фенвика и вместо декарток внутри будем использовать деревья Фенвика только по сжатым значениям. Такое решение уже работает достаточно быстро, в отличие от первого.
У меня зашло и на дереве отрезков, когда я понял, что инверсии слева и справа связаны, и начал считать только одну из них. Но все равно 3.5сек: посылка.
А еще у меня где-то там UB, видимо, потому что я ловлю WA1 на c++ 14, на котором мой прошлый код работал быстрее, чем на MSVC10.
Ошибка в разборе задачи D: "количество закрывающих скобок до данной". Правильно будет "после"
Спасибо, исправлю.
UPD: Уже исправлено :)
problem E:
(what i'm doing wrong?)
I also passed with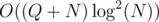 . Are you sure your solution with square root decomposition isn't actually
. Are you sure your solution with square root decomposition isn't actually 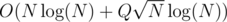 because if it is it actually makes sense that your
because if it is it actually makes sense that your 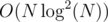 TLEd.
TLEd.
UPD: Your solution really is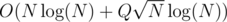 .
.
yeah, you are right
I passed in under 2000ms when i changed to BIT from segment tree with Order statistics tree in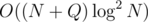
How would you use BiT instead?
You need two information to perform the swaps in every query:
At any index i, how many a[j] > a[i] such that j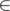 [1, i-1]. Let this value be x
[1, i-1]. Let this value be x
At any index i, how many a[j] < a[i] such that j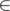 [i+1, n]. Let this be y
[i+1, n]. Let this be y
I only maintain the first information using BIT. The second information can be extracted as y = (a[i] - 1) - ((i - 1) - x)
25530551
Does the ordered tree act as multiset? Can we erase single value from ordered tree as we can delete a single value from multiset using iterator.
logx has a higher growth rate than sqrt(x) for larger inputs
nooo... its just some hidden constant in pb_ds and segment tree
I have a completely different algorithm that runs in time O(n log n + q sqrt(n)). It's here: 25590906 It is much simpler than the one in the editorial.
Draw the permutation as a 2-D plot. The key things that you need to be able to do are to (1) count the number of points below and to the left of a query point and (2) insert and delete points into the plot.
So we use a sqrt(n) decomposition of the plot into sqrt(n) by sqrt(n) squares of size sqrt(n). For each square we keep the number of points in it. We also keep a hierarchy of squares doubled in size. So there are .5 log n of these levels.
To solve a query we first note that there is an ell-shaped part that is that is outside of the squares described above. These can be counted in O(sqrt(n)) time. We maintain the permutation and its inverse. So the horizontal part of the ell (and the vertical too) can be counted row by row. Now to count the number of points in the squares we peel off possibly the top row and column and just count them. Now we move into the next level of boxes that are twice as big. The total time for this count is therefore O(sqrt(n)).
Inserting and deleting from the boxes is easy. Just make a pass through the levels. This takes O(log n) time.
This is truly one of the best editorials on CF till date. Giving hints and then the complete idea to the question is a good way to help us improve ourselves. Also, giving reference code in three different languages is a very appreciable effort. Congratulations to the writers of the contest for this excellent editorial and we hope to look more such editorials in the future.
Can anyone help me get rid of that 1e018 in 9th test case in problem C. 25537798 There are other submissions where the same formula is used but have an AC.
In problem C why do we have to binary search up to 2e9 not 1e9(it give WA)?Look at my submission with 1e9(25537413) and 2e9(25538410)???
for test case n = 1e18 m =1 ans is greater than 1e9 (approx. sqrt(2)*1e9)) put n,m values in the equation you will get maximum possible ans for the problem n — m <= k * (k + 1)/ 2
Can someone help me with the proof of — 785D — Anton and School — 2 , I am not getting the explanation given in tutorial . Thanks in advance
Where didn't you undestand it? I'll try to explain it better.
this part,
this formula also means the number of ways to match the string with the sequence of zeros and ones of the same length
Consider the number of ways to make a sequence of length x + y with x ones and y zeros. Won't it be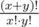 ?
?
Later, it's explained how to match an RSBS to every such sequence.
Is empty RSBS included in the answer?, e.g. for n=3,m=3 and string ((( ))), we include empty RSBS corresponding to 111000.
Yes, in the simplified version an empty string is included to the answer. Later in the solution, there won't be empty RSBS, because it will contain the iterated opening bracket.
It's kind of equivalent to stars and bars also.
I understand the significance of (x+y)C(x) but I don't know how the author originally came up with it. I had the formula given below in mind, but I don't know how to reduce it. xC1*yC1 + xC2*yC2 + xC3*yC3 +....+ xC(min(x,y))*yC(min(x,y)) I would appreciate it if you could please explain the formula using stars and bars. Thank you!
I couldn't think of any intuitive way of explaining the problem from a stars and bars perspective. I'm just noting that its equivalent.
write xCi as xC(x-i).
Observe that sigma(xCi*yCi) is coefficient of a^x in (1+a)^x * (1+a)^y.
Convince yourself that x+yCx -1 is your reduced from.
IDK why in editorial -1 is absent.
In editorial it is mentioned
But we also have an additional condition: we must necessarily take the last opening bracketThus we are interested in sigma{ xCi * (y-1)C(i-1) ) } = (x+y-1)Cx
[from i=1 to i=min(x,y)]
How do you justify the statement " Also opening brackets appear earlier than closing brackers " ??
I think it's obvious because in the simplified version we deal with the sequence like "((((...((()))))))))...))))" and every its subsequence will contain opening brackets earlier than closing brackets.
Thanks a lot !! I forgot the earlier explanation of simplified version .
Has anyone got AC in E using segment tree with multiset(supporting order stats)? I am getting TLE on #7.
TheTerminalGuy did, I guess. Here's his code. 25524777
3978ms seems quite a risk. The same solution may not pass again.
My code, 3337 ms.
cin / coutare to blame mostly.I too used cin/cout. I guess the time is due to the find function being called every time before erasing some value. As we have inserted tge value in set we can be sure that it will be present in set and remove it without worrying about runtime error.
Было бы очень здорово, если все авторы оформляли разбор так же, как и вы. Спасибо!
if problem E2 is data structures, it may be not hard to solve =))
My funny task A solution.
Also fan fact, that all task contains test case with "404" answer.
Haha! That is awesome, I had to stare at it for quite a long time to figure out how it worked. Excellent practice, thanks. May I ask how you fit that polynomial function?
I know your program was meant to be cool and not short, but anyway it made me think of writing something where the main logic was in a one-line formula, like yours.
So here's my "shortest code" submission, 127 non-whitespace characters (http://codeforces.net/contest/785/submission/25567260):
Would love to see shorter solutions .. in any language!
25547848 — just one line in python2
25745756 — just minified your code (without any thinking, only deleting unnessesary code)
Knew people would make it shorter but not THAT MUCH shorter. :-O :-)
Presentation of the editorial is really amazing... I think I'd never seen that before. Thanks a lot.
for question E Can we have a 2D BIT where BIT[x][y] where x will denote block no and y is actual number depending on given input.Then each query is solved in sqrt(N)+log(block)*log(N) and updates also in sqrt(N)+ log(block)*log(N). Correct me if I am wrong..
Very detailed & useful tutorial. Thank you very much!
First time in my whole journey (which is albeit short), I have seen an editorialist with so much creativity and patience taking so much interest in really explaining the solutions in a comment. It's sad how whistle blogs about complaining all about this contest. More power to you, gepardo.
Thank you :)
D is a very nice especially if one derives it without using the identity directly! Thank you for this problem.
I tried to solve problemE with segment tree plus ordered multisets but I am getting TLE on test 7.
The complexity of build function in my code in O(N * LOGN * LOGN * C). where C is the constant factor in segment tree.(C ≈ 4).
http://codeforces.net/contest/785/submission/25568923
Is there any way to optimize the build function.
What do the query1 and query2 methods do?
query1 calculates no of elements greater than val in ranger l to r and query2 calculates no of elements less than val in ranger l to r.
These 2 values are connected.
Suppose you have the element
xin the positioniin the array and you know the answer to one of the queries, e.g. there areanselements greater thanxin[1,i-1]. This necessarily means there arei-1-anselements smaller thanxin[1, i-1]. Since the total amount of elements smaller thanxisx-1, therex-1-(i-1-ans) = x-i+anselements smaller thanxin[i+1, N]. Thus, the total amount of inversions isx-i+2*ANS.This thing should reduce the constant of your solution. Also, don't use long long everywhere — this slows down the solution, which already runs pretty close to the TL.
Thanks for this idea but I want to reduce the complexity of build function which works in O(n * log(n)2 * c) because for 7th test case , even the build function is not able to execute in 4s.
Does it? I just ran your build() function of CF for 250000 and it seems to take about 1.3s.
Is there any divMod explanations? I don't understand how it works. Thanks
Is there any divMod explanations? I don't understand how it works. Thanks
divModis a function that computesa / bmodulomAt first instead of dividing it computes
(a * inv(b)) % mwhereinv(b)is an inverse element forb. Inverse element can be computed using an extended Euclidian algorithm. You can learn more about this hereThank you! That article is very easy to understand.
why is it low+m and not the midvalue+m? in 785C
Because I write the binary search in this way. I exit from the binsearch when
l=r. So the answer will be stored obviously inlCan Someone explain me why number of total possible valid sub sequence is x+yCx as explained in Editorial in 4th Question ? I am not able to understand that
Which part of the editorial you don't understand? I'll try to explain it better.
"At first, let's simplify the problem: let our string consists of x + y characters, begins with x characters "(" and ends with y characters ")". How to find the number of RSBS in such string?
Let's prove that this number is equal to x+y C x.
This is what I am not able to understand. If we take a string that consists of x + y characters, begins with x characters "(" and ends with y characters ")", then how total number of RSBS is (fact(x+y) / fact(x)*fact(y) ) ?
There's a proof in the editorial. What exactly you don't understand in it?
I didn't understand how did you decide to represent which bracket with 0 and which with 1. and so I am not able to understand the proof. Sorry if this is silly but I seriously do not get it
OK. Let's take ANY sequence of x ones and y zeros. Now write it under the bracket sequence in the following way:
Now let's take opening brackets under which we have zero and closing brackets under which we have one (green brackets on the picture).
Now, we must prove that number of opening brackets will be equal to number of closing brackets. How to do it? Suppose we have z zeros under opening brackets and, therefore, x - z ones (because we have x opening brackets)under opening brackets. So the rest of ones are under closing brackets. Their count will be x - (x - z) = z (because we have x ones. So we have equal count of opening and closing brackets. So we took an RSBS in this way.
Now more understandable?
Okay.. Now I completely got it.. Now it is much easier to visualize for me for the further part of your tutorial. So thank you so much for tolerating and quickly answering to my silly doubt. Truly appreciate your quick reply to each and every comment. Thank you so much.
Does the difficulty of this task correspond to Div2?
I think yes, because 94 people in Div. 2 solved it. But I agree that it's harder than Div. 2 D level.
How do we assign 0s and 1s?
You can choose any of the sequences that contain x ones and y zeros.
in the problem:B we have to calculate the max distance between the periods that is the time between end of first period and start of second period but in the editorial why we are calculating int minR1 = infinity, maxL1 = -infinity; int minR2 = infinity, maxL2 = -infinity; for (int i = 0; i < n; i++) { maxL1 = max(maxL1, a[i].first); minR1 = min(minR1, a[i].second); } for (int i = 0; i < m; i++) { maxL2 = max(maxL2, b[i].first); minR2 = min(minR2, b[i].second); }
maxL1, maxL2 — maximum left ranges in chess variants and programming variants
minR1, minR2 — minimum right ranges in chess variants and programming variants
Then we use them for both cases. In first case we need the distance between minimum right chess range and maximum left programming range. So we simply use
maxL2 - minR1. The same in the second case.In problem 785D Anton and School 2 for the case when we have x opening brackets and then y closing, total number of RSBS according to the editorial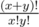
Should we subtract 1 from it? (case when we have x ones in the beginning and then y zeros as I understand is empty sequence which is not RSBS according to the statement).
I was thinking in a bit different way about number of RSBS when we have x opening brackets and then y closing, if we sum over the length of first half we can find that number of RSBS is:
But I don't know how to simplify this one. Maybe someone was doing similar things and achieved result?
Yes, because in this formula we count an empty string as an RSBS. But in the further problem we don't have to subtract 1, because we always take the last opening bracket, so RSBS won't be empty.
Do you know is there a way to simplify this sum: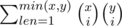 ?
?
No, unfortunately I know a normal way how to simplify this to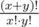 . I came to this simple formula bruteforcing the answer and then found that beautiful proof. So I didn't try to simplifity such expression.
. I came to this simple formula bruteforcing the answer and then found that beautiful proof. So I didn't try to simplifity such expression.
Hi did you find any way to simplify this equation, Even the approach I am thinking boils to this equation
This may help — Vandermonde's Identity
We can count this as taking i objects from a pile of x objects, and y - i objects from a pile of y objects, where i varies from 0 to Min(x, y). This is basically equivalent to taking a total of y objects total, from a collection of x + y objects. Hence, our summation above can be rewritten as:
Multiply (1+x)^n1 and (x+1)^n2 See its binomial expansion. You will find the required ans to be coefficient of n1+1 in (1+x)^(n1+n2). Again use binomial to find coefficient. You will get formula given in editorial. Here n1=x, n2=y
I just solved problem E today. I can see somebody here has same approach with me: using Balanced BST (I choose Treap) on segment tree. My second submission run in O((N + Q) × log2(N)) time complexity and I got TLE. Then I reduce my solution to O(N × log(N) + Q × log2(N)) time complexity and got AC by reducing the build tree step to O(N × log(N)) time. More over, each node is a treap can be built in O(N) time. Hope this help someone implement this problem easier.
Isn't it the algorithm for Problem D?
But I am getting Memory limit exceeded on test 6 verdict :(
Consider how much memory the line
consumes. It'll be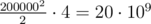 bytes, which is about 20 GB. It won't fit any time limit.
bytes, which is about 20 GB. It won't fit any time limit.
Yes, it is, but you need a way to find the number of combinations faster. To do this, you can look at my code, which is in the editorial.
To do this, you can use a naive formula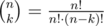 . To calculate this fast, you can do the following:
. To calculate this fast, you can do the following:
Precalculate all the factorials under 106 by modulo.
Learn how to divide by modulo. Dividing by modulo means multiplying by an inverse element. How to find the inverse element, see the article
P. S I recommend you not to place you code directly in the comment. You may place a link to submission instead, or place your code to ideone or pastebin and provide a link to it. Or you can use spoilers, like this:
Thank you so much for the link :)
P.S:The comment has been edited as it is recommended.
Thank you so much for the great editorial.
For modular multiplicative inverse by extended Euclidean algorithm, we have a statement x = (x % m + m) % m. This will give an element in the range [0,m), right? My doubt here is can the modular inverse be negative. Else we could have written x = (x % m) directly. Sorry if this doesn't make any sense.
No, the modular inverse cannot be negative. When we deal with arithmetics by modulo, we always take integers in the
[0;m)range.Hello, can some tell me what is wrong with this solution with C problem? 25806694
Thanks in adavanced.
In the 7th test case your
l > 2e9, sol > rand you don't enter the binary search and just printm+1(that isl).why to use the logn time complexity ? This can be done in O(1). We dont need to use the binary search.
At the end of mth day the no of grains in the barn is n — m; from the next day it will be like (m — (m+1) , (m — (m+2)), ... , (m — (m+k)) which can be written as k * (k+1)/2. lets formulate the equation n = (k *(k+1))/2. hence k^2 + k — 2*n = 0; the root is (-1 + (sqrt(1 + 4*2*n))/2. let this be s. if(s*s + s < 2*n) then add a day. day = m + s is the answer.
785D — Anton and School — 2
I think this sentence is not correct in solution : number of RSBS in string that begins with x characters "(" and ends with y characters ")" equal to ( x + y)! / ( x! * y! )
it must be : ( ( x + y)! / ( x! * y ! ) ) — 1
Why we subtract 1 ?
In solution written that : formula also means the number of ways to match the string with the sequence of zeros and ones of the same length, which contains exactly x ones
Lets look picture in example : ( ( ( ) ) ) )
one combination is 1 1 1 0 0 0 0 If we create string with following algorithm which is written in solution : all the opening brackets that match zeros and all the closing brackets that match ones Resulting string will be empty string. And empty string is not RSBS. And this means we must subtract 1 . But Code work fine. Because in code we write ( x + y-1)! / ( x! * (y-1)! )_ ( explained in solution ). This prevent taking empty string
Can someone help me with my solution of Problem E ? Link: https://ideone.com/500vNF I am using segment tree with each node having a set .
In the solution of problem C,why is the upper limit of binary search 2e9??
Because the maximum possible answer is around $$$1.414\cdot10^9$$$. But I just took a larger boundary for binary search.
thanks....