Yes, exactly. In D we have this: if m ≥ 2n + 2, we construct the answer as a rectangle 1 × x and a number of unit squares. Otherwise if m < 100, do a straightforward dp. Otherwise iterate for possible rectangle a × b to obtain m ≥ 2n + 2 in remains. We checked that this works on the contest by a straightforward dp for reasonable values of n, m.

I have O(n^2*logn) DP.

We need to take a set of pairs a,b such that sum(a*b)=x and sum(a+b)=y. a=1,b=1 adds 1 to x and 2 to y, so our DP can be: for a given parity of y, and a given value of 2x-y, what is the smallest possible y? We have O(n) states and O(nlogn) possible rectangles for transitions.

OMG. Stupid knapsack in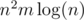 with bitsets works 0.2 seconds.

We need to choose for each cell if it's covered by row or column, and in the end for each row or column with 2 different symbols multiply the answer by 2. Do dp[row][mask], where row means that we already chose cells for first row rows and mask stores for each column how many cells in that column we did not choose yet(it's  ≤ 2, so there are only 3ⁿ masks).

M: Sum of depth of subtrees for all vertices is O(n). So you can do whatever you want if it is linear with small constant. Looks like problem with bigints is that constant isn't so small.