How can i optimize my code?
#include <bits/stdc++.h>
using namespace std;
int n, m, a[30005];
int bs;
vector<int> block[300];
int sqrtDecomposition(int l, int r, int v){
if(l / bs == r / bs){
int cnt = 0;
for(int i = l; i <= r; i++){
if(a[i] > v) cnt++;
}
return cnt;
}
int cnt = 0;
for(int i = l; i / bs == l / bs; i++){
if(a[i] > v) cnt++;
}
for(int i = r; r / bs == i / bs; i--){
if(a[i] > v) cnt++;
}
for(int i = l / bs + 1; i < r / bs; i++){
cnt += (block[i].end() - upper_bound(block[i].begin(), block[i].end(), v));
}
return cnt;
}
int main(){
cin >> n;
for(int i = 0; i < n; i++){
scanf("%d", a + i);
}
bs = sqrt(n);
for(int i = 0; i < n; i++){
block[i/bs].push_back(a[i]);
}
for(int i = 0; i < 300; i++){
sort(block[i].begin(), block[i].end());
}
cin >> m;
for(int i = 0; i < m; i++){
int l, r, v;
scanf("%d %d %d", &l, &r, &v);
l--; r--;
int ans = sqrtDecomposition(l, r, v);
printf("%d\n", ans);
}
}










Sqrt decomposition is probably just to slow here
(30000+200000) * sqrt(30000) = 39837168
should pass the time limit.
Upper_bound has complexity of so your solution's complexity is
so your solution's complexity is 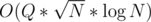 which will fail for KQUERY. If you submit it on KQUERYO (the online version at spoj) it should pass.
which will fail for KQUERY. If you submit it on KQUERYO (the online version at spoj) it should pass.
The total time complexity turns out to be nlogn + (q + n)*root(n) that is: 30000*log(30000) + (30000+200000) * root(30000) = 446100 + 39837168 = 40283268 ~ 4 * 10^7. Now about 10^8 operations are carried in one second and time limit for this problem is 0.184s. Therefore upper bound on permissible number of calculations are 0.184*10^8 ~ 2*10^7 (> 4*10^7). Thats why Mo algorithm gives TLE.
You can do this by two pointer technique.
hmm... right..
any idea to optimize?
I think you can compress numbers and store prefix sums for each block.
You can use BIT instead of Mo
1) Make a vector of pairs and put (array element , its index) and sort it in reverse order (that is greater element comes first).
2) Now sort queries such that query having larger K comes first.
3) Now use 2 pointer technique, before processing a query update in the BIT (add 1) to all indices having elements greater than k of this query. And now query on the BIT.
Complexity will be O((n+q)logn).