Aeon's blog

GP of Tatarstan
By Aeon, 8 years ago, In English

Lets discuss problems.

How to solve C?

  • Vote: I like it
  • +36
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

In problem B, there're no restrictions of coordinates (I can only find the assurance of coordination). However, I got AC by adding the restrictions of maximal cooordinates to WA code after contest.

Is the checker of B correct?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    I got a WA for the same reason. It is not mentioned in the statement that whether your results should be in [-1e9,1e9]. Maybe they forgot to...

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Strange. I didn't check for that and got accepted without any problems. The problem asked for the answer with absolute precision, so maybe, you don't have enough precision for such big coordinates, but enough, when they are smaller than 109?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Is the checker of B correct?

    For first sample, we output (5.52, 7.36), (-6, 4) and (10, -8), but got WA on test 1...

    And we thought it's a valid solution. Not sure whether the checker is correct, or we misread the problem.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      The checker was wrong! It required that (X,Y,Z) be a clockwise traversal around the triangle. And this condition is not part of the problem statement.

      Note that if there is any solution then there is one in clockwise order. You can simply reflect the triangle about the line through A and B to reverse its orientation.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve E?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Let's divide the K digits into N - 1 groups. We add a two-digit number xy to the set of working stations if x and y are in the same group. It's clear that this is a valid set. It seems the optimal solution is always of this form. Does anyone have a proof?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +25 Vote: I do not like it

      (I assume n ≤ k). First, we need to take numbers of form dd to deal with numbers dn.

      After that, let's look at rwo digits numbers as edges in directed graph with k vertices. Now consider increasing numbers (digits are in increasing order) and edges xy where x < y (edges xy, where x ≥ y, don't influence them), let's call them increasing edges.

      So, we want to take some subset of increasing edges in our graph so graph does not contain an undirected anticlique of size n. By Turan's theorem, minimum number of such edges is achived on union of (undirectedly) complete graphs of almost same sizes. Same for decreasing edges.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

We solved F using suffix array with O(n * n*m * log(n*m) ).

Is there any easier solution?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +44 Vote: I do not like it

    O(n2 * m2) brute force works...

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +2 Vote: I do not like it

      Wow. And why does it?

      Upd: It's easy: we ingore all string with lengths smaller than k. Now there are SUM/k vertices. So the asymptotic is much lower.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can use hashes instead of suffix array

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Hashes are slower.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it -18 Vote: I do not like it

        Our solution is O(n^3) 'cause we replaced O(n*m) parth with O(Log(n*m)) via hashes and it runs in 0.03 so who cares

        → Reply
»
8 years ago, # |
  Vote: I like it +18 Vote: I do not like it

How to solve K ?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it +3 Vote: I do not like it

    Let's learn how to find the boundaries of a "good" segment (that is, the segment where the current tile can go).

    Let's assume that some column L is located to the left from the column C where the tile appears. One can see that it's impossible to go to the left from L if num_rows - h[L] <= C - L or, equivalently, num_rows - C <= h[L] - L. The right hand side is a function in one variable L, so we can keep a segment tree with values h[i] - i for all valid i and find the left boundary of the "good" segment efficiently (finding the largest value of L such that the maximum of the [L, C] range is greater than a fixed value is a standard problem).

    We can find the right border in the same manner.

    Once we know the boundaries of the "good" segment, we can split it into two parts: [L, C] and [C, R], find the leftmost and the rightmost minimum for each range and pick the best one (we can keep one more segment tree to keep track of the minimum and its positions).

    A proper implementation uses O(log N) time per query.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +13 Vote: I do not like it

C: First, let's focus on solving this problem for one query and small n. We can assume that all lower bounds for heights are 0 (otherwise we can just subtract them from A and corresponding upper bound). By well known formula, there is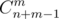 ways to express m as sum of n non-negative integer summands (if order matters). Why answer is not 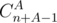? Because we could violate some restrictions. To deal with this, we will use inclusion-exclusion principles. Number of ways we can violate restrictions h1, h2, ..., hk on heights of some buildings and still sum up to A, is 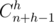. where A ≥ h = h1 + h2 + ... + hk + k (if A < h, it is zero). If multiset of all building restrictions is H and 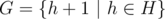(counting with multiplicities), then we want to know value of .

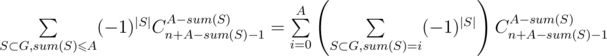So, to solve this problem, we want to recalculate coefficients in brackets after each query of type 1 (then we can find answer in O(A) for each query, because we can precalculate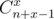 for 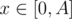before answering any queries).

Now, we just want to calculate this coefficients after each query of type 1. Because there are only Q = 30 queries of first type, buildings are always separated in at most 2Q + 1 segments with same height restrictions (it's conventient to think that there is also starting restriction on heights of all buildings: they should be in range [0, 1000]). The other way to put is that there are at most 61 pairs of numbers di and ki, that there are di buildings with upper bound on height equal to ki and .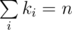

After that, we can just do following dp, which is somehow hard for me to explain in words:

Code

It works in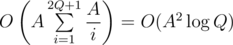 , so total complexity is .

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

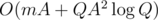    Nice, I thought FFT was necessary.

    If you use FFT the TL is tight. My initial solution with O(Q2 logA) FFTs got TL (maybe because my FFT was slow, did anyone get AC this way?), and a solution with O(QlogA) FFTs got AC.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      There is solution that works in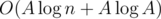 per query of the 1st type and answers in O(1) to queries of the 2nd type.

      Detailed analysis is quite long, but here is some hints:

      To achieve this complexity one should be able to compute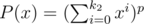 and 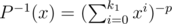(where p = (r - l + 1) is range of houses, k1 — old limits for heights and k2 is new limits) in 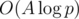and just multiply obtained polynomails to the resulting polynomial.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      My solution with O((Q * A * logA) * (logN + Q)) passed quite easily under 1 second.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      I did accept it after contest with much optimisations. It was crucial to change long long mod = ... to const long long mod = ... :) And do 2 FFTs instead of 3 when possible.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can any one explain the fft based solution?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
          ← Rev. 3   Vote: I like it +8 Vote: I do not like it

          You need to multiply n polynomials of type xc + xc + 1... + xd. There are at most q + 1 distinct polynomials, so you can do fast exponentiation. The modulo allows to use integer FFT, since it is like a × 211 + 1

          → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve I?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Binsearch on 'K': take all prefixes of cyclic shifts of len K, build bipartite graph between strings and these cyclic shifts(there's an edge from string to every its cyclic shift), check if maximum bipartite matching is of size N.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Let's assume that K is fixed. We can ignore all strings shorter than k (they're unique, anyway). Let's imagine that we can construct a bipartite graph, where there's a vertex for each string in the left part and a vertex for each cyclic substring of length k in the right part. If we add edges from each string to its substrings in this graph, we just need to check if this graph has a matching that covers all vertices in the left part. There're at most N vertices in the left part and at most S edges in this graph (where S is the total length of all strings).

    We can binary search over k and use a standard algorithm to find a matching. The time complexity of this solution is O(N * S * log S).

    The only question is how to build such a graph efficiently. One can use hashes or some suffix data structure to do it.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We can solve this problem bit faster than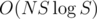 . If a string has at least N different substrings of length k, we can ignore the string when considering bipartite matching. This reduces the number of edges in the graph to O(N2). Thus the overall time complexity becomes .

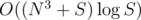    The correctness of this algorithm is confirmed by Hall's Theorem.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +15 Vote: I do not like it

How to solve Problem G?

We have thought about some complex ways to do but there is no time left.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    Sort points by angle from the river source. Go there using the "outer convex hull", and back using the remaining points (both parts in order of angle from river source).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      There will be no solution if and only if this construction doesn't work?

      How can we prove it?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        If you have two points from this convex hull then you must have also visited every point in the convex hull between them. So one of two paths should contain all points from this convex hull.

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +15 Vote: I do not like it

        Yeah, what -XraY- said. Also note that here we need the convex hull that includes the intermediate points on the sides.

        There's also a slightly tricky case when the inner polyline passes exactly through the river source, and there are many points on that line: in that case we must make sure to order the points before passing the source towards it, and after parsing the source away from it.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How to solve H and N? For N we tried finding which of the edges of the triangle are visible from the hovercraft and then doing a ternary search on them to find a point which would give the shortest time. For H we tried to model the situation as a graph and find the shortest path between the first and last nodes, however we ran into a problem with continuous blocks of type 2 rows. We tried to sort them in some order which we thought would give the best answer, but got WA.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Ternary search in N is ok. But you should consider all edges of triangle and run ternary searches separately for each one. Because sometimes it is better to enter into triangle from the rear side.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    H:

    Finish position can be transformed to [n+1]-th row of type 1.

    It can be shown, that there are only 4 optimal orders of 2-type groups: [ascending, descending] × [all on left half, all on right half].

    We get AC with dp, but shortest-path search algorithm is dp too, there is shouldn't be a difference.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you! :)

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How did you guys solve problem A so fast? I had to figure out primes for 1/p1 + 1/p2 + ... + 1/pn = 1, and after that combine them to form solutions for k > 1. It was not obvious to me...

→ Reply