Hi,
I am trying to implement a 2-D segment tree, seg with N = 100000... The catch is that I only need to get the query answer for Q(100000) nodes say query(i,j) : denoting the value in seg[i][j]... but i need to online (lazily) update the seg tree, seg[lx...rx][ly...ry].
Can anyone help me with this problem?











Auto comment: topic has been updated by zeref_dragoneel (previous revision, new revision, compare).
What is the problem with using a dynamic 2D segment tree?
Another way which is much easier and faster is using 2D compressed Fenwick tree but it will be offline.
http://www.spoj.com/problems/XXXXXXXX/
Did not get to any solution other than dynamic 2D segment tree with range updates.
Well in this problem you don't need an online solution. As I said you can use 2D compressed Fenwick tree. You also can replace the inner dynamic segment tree in your solution with a compressed Fenwick or Treap. In such a way you could make the solution faster and make it use less memory. If you didn't get what I meant by compressed Fenwick, here is an implementation. If you didn't get what I meant by "replacing the inner segment tree" you can take a look at my solution to this problem (solution). I used a similar approach. It won't be hard to figure out how to reapply the same approach to the problem you've linked.
Actually why do you need range update?
Lets find for every i the last occurrence of a[i] and denote it by left[i] (if i is the first occurrence then left[i] = - 1).
Then the query becomes:
given L, R, find the sum of a[i] for L ≤ i ≤ R such that left[i] < L. This can be done with range query in any 2D data structure. So the overall query complexity is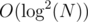 .
.
And in the update you should change the left value of the next occurrence of a[i] and then make O(1) point updates in the 2D data structure. So the overall update complexity is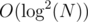 .
.
PS: Also in the update you should change the left value of the next occurrence of V (V is the value we update the position with). And also of course we need to update the left of the current position we update and do a point update in the data structure for every update of left we make. Overall we should make 6 point updates in the 2D data structure.
Can you please elaborate on "given L, R, find the sum of a[i] for L ≤ i ≤ R such that left[i] < L. This can be done with range query in any 2D data structure."?
On one dimension you have the indexes in the array and on the other one you also have the indexes in the array. Then the query becomes:
Find sum in sub-rectangle with upper left point (L, 0) and lower right point (R, L). And when we do update we update point (i, left[i]) with value a[i].
Just so that I understood it correctly, is this similar to a segment tree where each node is a treap so node (l,r) gives the treap for present indices in [0, r].
except you are having a compressed fenwick tree instead of a treap.
Exactly. That's why I mentioned that it also can be done with treap, but unfortunately I think it will not be fast enough.
Thanks a lot. You helped me a lot understanding a new datastructure. :)