Has anyone looked into the problem of determining the algorithmic complexity of a solution to a problem using the maximum solving time on test cases of different sizes? I imagine you could use least squares where the basis functions include some polynomials, some powers of log, an exponential and products of these up to a certain fixed size. It might be an interesting thing to calculate for complex solutions.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 166 |
| 2 | maomao90 | 163 |
| 2 | Um_nik | 163 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 160 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | nor | 153 |
| 9 | Dominater069 | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 17.11.2024 20:51:13 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










The biggest problem that I can see here is I/O time. What I mean is that solution with only N in the input and the same complexity solution, but with array of N numbers will be quite different in their run time.
solution with only N in the input and the same complexity solution, but with array of N numbers will be quite different in their run time.
I might be missing something but won't these differences be taken into account by different constant terms? The way I am thinking such a program would output something like instead of leaving it in O form and you could compare the different coefficients of the
instead of leaving it in O form and you could compare the different coefficients of the 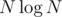 terms in the I/O solution and the vector solution.
terms in the I/O solution and the vector solution.