Задачи раунда были подобраны Олегом snarknews Христенко.
Задача A. Арифметическая задача
В данной задаче требовалось написать ровно то, что требуется в условии — начать перебирать целые числа, начиная с единицы, дойти до первого числа, которое не делит n, и вывести его. Несмотря на то, что само n достаточно больше, это работает быстро, так как в ограничениях задачи ответ всегда не превосходит 22 (наименьшее общее кратное всех целых чисел от 1 до 23 это 5354228880, что уже превосходит максимально возможное значение n).
Это была одна из самых простых задач контеста, в которой, тем не менее, многие участники по причине спешки на первых минутах контеста получали WA 4 из-за того, что машинально перебирали ответ не от 1 до бесконечности, а от 1 до n, что, конечно же, не работает при n = 1 и n = 2. Особенно, наверное, обидно допустить такой баг, отправив задачу втёмную :)
Задача B. Построение четырёхугольника
Наряду с задачей А данная задача была одной из самых лёгких. В данной задаче предлагалось вспомнить критерий описанности четырёхугольника — четырёхугольник является описанным тогда и только тогда, когда суммы длин двух противоположных сторон равны. Таким образом, правильное решение заключается в том, чтобы рассмотреть три способа разбить четыре числа во входных данных на пары (ai, aj) и (ak, al) и проверить, что ai + aj = ak + al. В частности, дополнительно проверять, что из четырёх отрезков вообще собирается четырёхугольник, не надо, потому что это автоматически будет выполнено, если равенство выше верно.
Задача C. Циклопы и линзы
Данную задачу можно решить с помощью какого-либо жадного соображения. Будем говорить, что циклопы спарены, если они носят линзы из одной пары. Очевидно, мы хотим максимизировать количество спаренных циклопов.
Рассмотрим циклопа с минимальным li, пусть это значение равно x. Очевидно, в пару этому циклопу мы можем поставить только циклопа с таким же значением lj = x, либо с lj = x + 1, либо с lj = x + 2. Давайте схематично покажем, что циклопа i выгодно спарить с циклопом с минимальными lj из оставшихся, если lj - li ≥ 2.
Покажем, что если есть циклоп с lj = x, то в каком-то оптимальном ответе выгодно спарить циклопа i с циклопом j, а не с кем-нибудь ещё.
Если циклоп i не спарен ни с кем, то просто поставим циклопа j в пару к нему, таким образом мы либо одну пару циклопов потеряем (если j находился в паре с кем-то), а пару (i, j) образуем, либо же мы спарим двух неспаренных циклопов (если j был тоже одинок). Видно, что это не ухудшает ситуацию.
Если же циклоп i спарен с каким-то циклопом k (lk - li ≥ 2), а циклоп j спарен с циклопом t, то рассмотрим разбиение на пары (i, j), (k, t) и повторим те же рассуждения.
Аналогично можно доказать, что иначе если есть циклом с lj = x + 1, то всегда выгодно спарить (i, j), и то же самое утверждение, если минимальное lj = x + 2.
Таким образом, мы получили простой жадный алгоритм (гораздо более простой, чем его строгое обоснование!): мы идём по циклопам в порядке возрастания li и пытаемся спарить каждого очередного циклопа со следующим, если это возможно. Если не получилось, покупаем пару линз только на текущего и переходим к следующему циклопу, иначе покупаем на них одну пару линз на двоих, и переходим дальше. Данное решение работает за время сортировки последовательности входных данных.
Задача D. Два преобразования
Во-первых, оставим от каждого числа во входных данных только его остаток от деления на 2. Отдельно разберём случай n = 1, который не доставляет особых трудностей.
Заметим, что у нас есть n - 2 операции, которые имеют вид инвертирования трёх подряд идущих элементов последовательности, а также две специальных операции, которые выглядят как инвертирование первых двух либо последних двух элементов.
Очевидно, порядок применения операций не имеет значения, а значит, каждую операцию мы применим не более, чем один раз. Пусть мы, для определённости, делаем все числа чётными, то есть, нулями. Переберём два варианта: либо мы будем использовать инвертирование двух первых элементов, либо нет. Если мы решили использовать, инвертируем их.
Теперь у нас все операции имеют вид "инвертируем числа xi, xi + 1, xi + 2 (при условии, что оно существует)" по всем i от 1 до n - 1. Заметим, что теперь однозначно определяется, надо ли использовать каждую следующую операцию: действительно, если x1 = 1, то мы точно будем использовать первую операцию, иначе точно не будем. Инвертируем x1, x2, x3, потом, глядя на x2 мы однозначно понимаем, надо ли использовать вторую операцию, и так далее.
Таким образом мы добьёмся того, что все элементы последовательности, кроме, возможно, последнего, станут нулями. Если последний не стал единицей, значит зафиксированный нами вариант использования операции над x1 и x2 был неудачным, и в нём вообще невозможно добиться требуемого. Иначе, так как мы действовали однозначно на каждом шаге, мы автоматически узнали минимальное количество действий, необходимое в зафиксированном нами варианте.
Найдём общий ответ как минимум из ответов для двух вариантов того, используем ли мы операцию над x1 и x2 в начале, или нет.
Аналогично поступим, чтобы сделать все числа нечётными. Сложность полученного решения — O(n).
Задача E. Точки и окружности
У данной задачи есть два подхода к решению. Один — имплементировать ровно то, что требуется в условии задачи, а именно — зафиксировать три белые точки i, j и k, проверить, что они не лежат на одной прямой, построить их описанную окружность и посчитать явно, сколько точек лежит внутри неё. Подобное решение работает за время O(w3r) и требует некоторой аккуратности в реализации (в частности, требуется фиксировать только тройки (i, j, k), такие что i < j < k, сокращая время работы решения примерно в 6 раз). Ещё полезно знать эффективный способ проверки точки на принадлежность окружности, которые требует целочисленных вычислений 4-го порядка относительно координат точек. Можно показать, что точка p = (px, py) лежит внутри окружности, описанной около точек a = (ax, ay), b = (bx, by), c = (cx, cy), тогда и только тогда, когда знак определителя
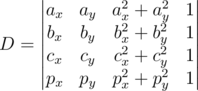
совпадает со знаком минора
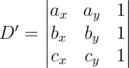
Данное решение требует только вычислений в целых числах, является абсолютно точным и весьма эффективным.
Данная задача также допускает решение за время 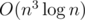 , использующее преобразование геометрической инверсии, но его мы подробно разбирать не будем, так как оно работает примерно столько же, сколько и решение за четвёртую степень. Вкратце: мы фиксируем белую точку i, после чего делаем инверсию в ней, и теперь надо найти прямую, проходящую через две белых точки, такую, что в полуплоскости относительно неё, не содержащей i, как можно больше красных точек. Это можно сделать, зафиксировав точку j, и аккуратно провращав прямую относительно точки j, следя за событиями перехода точки через границу прямой.
, использующее преобразование геометрической инверсии, но его мы подробно разбирать не будем, так как оно работает примерно столько же, сколько и решение за четвёртую степень. Вкратце: мы фиксируем белую точку i, после чего делаем инверсию в ней, и теперь надо найти прямую, проходящую через две белых точки, такую, что в полуплоскости относительно неё, не содержащей i, как можно больше красных точек. Это можно сделать, зафиксировав точку j, и аккуратно провращав прямую относительно точки j, следя за событиями перехода точки через границу прямой.
Задача F. Обслуживание сети
Данная задача сводится к задаче нахождения потока минимальной стоимости.
Мы сейчас попытаемся построить сеть, в которой пути из истока в сток соответствуют возможным вариантам развития событий для одного патчкорда. Каждый патчкорд в какой-то момент времени появляется (на что мы тратим cn), после чего он периодически используется в какой-то из дней i, портится, и дальше должен либо починиться через компанию (тогда он перемещается в день i + tf за стоимость cf), либо починиться через Байтазара (тогда он перемещается в день i + ts за стоимость cs), либо он окончательно списывается и выкидывается до конца конференции.
Давайте это интерпретировать следующим образом: рассмотрим сеть, в которой есть исток s, сток t, а также n пар вершин (1 + , 1 - ), (2 + , 2 - ), ... (n + , n - ), соответствующих дням конференции. Зачем каждому дню сопоставлять две вершины будет объяснено отдельно.
Скажем, что из истока s в вершину i - входит ребро стоимости cn и пропускной способности ∞. Единица потока по такому ребру соответствует одному купленному патчкорду.
Скажем, что из вершины i + в вершину i - ведёт ребро пропускной способности ri и стоимости - A, где A — некоторая положительная величина. Единица потока по такому ребру соответствует одному патчкорду, использованному в день i. Назовём рёбра такого вида важными.
Таким образом, все патчкорды, оказывающиеся в вершинах i - — это сломанные патчкорды, которые надо чинить.
Скажем, что из вершины i - исходит ребро пропускной способности ∞ и стоимости 0 в t. Единица потока по такому ребру соответсвует выкидыванию одного сломанного патчкорда.
Скажем, что из вершины i - исходит ребро пропускной способности ∞ и стоимости cf в (i + tf) + . Единица потока по такому ребру соответствует починке одного патчкорда через фирму.
Скажем, что из вершины i - анаологичнымбразом исходит ребро пропускной способности ∞ и стоимости cs в (i + ts) + . Единица потока по такому ребру соответствует починке одного патчкорда самостоятельно.
Наконец, скажем, что из вершины i + исходит ребро пропускной способности ∞ и стоимости 0 в (i + 1) + . Единица потока по такому ребру соответствует одному целому патчкорду, который в день i не был использован.
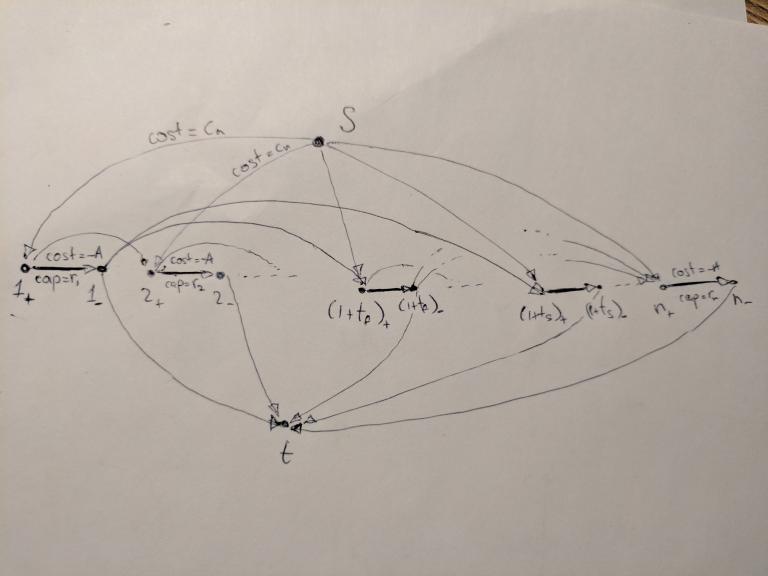
Любой корректный поток в такой сети соответствует какому-то набору патчкордов и стратегии их использования, но этот набор патчкордов, возможно, не до конца удовлетворяет потребности в каждый день. Нас интересуют только такие потоки, которые насыщают все важные рёбра. Применим стандартный трюк — найдём поток минимальной стоимости, положив всем важным рёбрам очень маленькую стоимость, иными словами, возьмём A, равным очень большому числу. Тогда итоговая стоимость потока будет равна - A·satcnt + opcost, где satcnt — количество насыщенных важных рёбер, а opcost — стоимость покупки/починки всех использованных патчкордов.
Найдём поток минимальной стоимости (обратите внимание, он не обязательно является максимальным потоком в данной сети). Несложно видеть, что такой поток в первую очередь максимизирует количество насыщенных важных рёбер, то есть, достигает требования, что в каждый день нам хватает целых патчкордов, а во вторую минимизирует затраты на соответствующий план использования.
Таким образом, мы получили решение, работающее за время одного запуска алгоритма нахождения потока минимальной стоимости в сети без отрицательных циклов. Алгоритм нахождения кратчайшего увеличиавающего пути с помощью Форда-Беллмана работает без особых проблем при данных ограничениях.











В Е еще можно построить KD-дерево по красным точкам и считать число точек внутри окружности с помощью него. Это вроде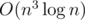 в среднем, и заходит с проверками на даблах влоб. Хотя видимо это все равно 4 степень в худшем.
в среднем, и заходит с проверками на даблах влоб. Хотя видимо это все равно 4 степень в худшем.
в задаче Б отсортировал массив по неубыванию и проверил, что a[0] + a[3] == a[1] + a[2]. Где ошибка?
Видимо, ошибка в реализации, потому что у меня такое же решение и зашло без проблем. По собственному опыту, могу посоветовать проверить правильность вывода "Yes", "No" — большие/маленькие буквы
Да, спасибо, нашел багу. Код Строчка 103 ничего не делает)))
ad E: Determinants are sorcery, inversion is dark sorcery. My solution in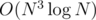 for non-wizards uses the fact that if
for non-wizards uses the fact that if 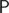 lies in the circumcirle of
lies in the circumcirle of  , then
, then 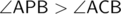 or
or 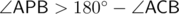 for
for 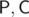 respectively on the same side and on opposite sides of
respectively on the same side and on opposite sides of  (collinearity is a special case). Angles can be computed using the law of cosines. If we fix
(collinearity is a special case). Angles can be computed using the law of cosines. If we fix 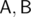 , the problem becomes sorting and two-pointer (well, 3-pointer if we split red points by
, the problem becomes sorting and two-pointer (well, 3-pointer if we split red points by  ) iteration. Precision wasn't an issue here thanks to additional constraints.
) iteration. Precision wasn't an issue here thanks to additional constraints.
В задаче E же можно перебрать пару точек, перебором найти 3ю точку, наиболее удаленную от прямой проходящей через первые две (вернее, две таких точки, одну над и одну под прямой), и рассмотреть, сколько красных точек входит в искомые окружности, O(N2 * (N + M)), нет?
Ограничиться двумя наиболее удалёнными точками недостаточно:
Видно, что если зафиксировать две точки, через которые нарисована прямая, то наилучшая окружность на этих двух точках будет маленькая.
Тем не менее, это не контртест против упомянутого решения, потому что оно сможет по-прежнему окружить все точки, выбрав в качестве опорных крайние слева и справа, но утверждение, во всяком случае, неверно.
Действительно. Пострессил свое решение, сделал два вывода.
1). У меня был баг, вроде бы я все время выбирал в качестве третьей точки первую из тех, которая не лежит на одной прямой с первыми двумя. И это зашло..
2). После того, как я это пофиксил, нашел следующий простой контрест:
Правильный ответ (0, 2, 3) таким решением не находится.
В F заходила следующая жадность (строгого доказательства нет, но контрпример не придумывается и она довольно интуитивна).
Переберем, сколько патчкордов мы купим. Их, очевидно, выгодно купить сразу.
Далее будем итерироваться по дням. Может случиться ситуация, что у нас не хватает патчкордов. Ее можно решить, отправив на ремонт патчкорды из прошлых дней. При этом мы сначала пробуем отремонтировать их сами (то есть использовать какой-то древний день, самый ранний из доступных), а если не получается — ремонтируем при помощи фирмы (используя самый поздний из доступных дней). Процесс несложно моделируется при помощи deque.
Код (Я спешил и написал за O((sum(r[i]))2), но не сложно модифицировать до O(sum(r[i])·n)
А в задаче D вообще может быть такое, что невозможно получить все четные/нечетные числа?
Да, например если исходная последовательность выглядит как
0 1.А для размерностей больше 2?
Например:
1 1 1 1 0В разборе задачи E минор D' вроде должен быть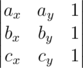
Вы правы, это была опечатка. Спасибо за указание!
I think problem E's D' is not correct. It doesn't pass first sample.
Is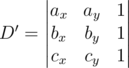 correct?
correct?
Yes, you are right. That is a typo, as it was already noticed in Russian version of the site. Fixed.
Geometric meaning of sign(D') in this formula is 2-d orientation of triple a, b, c.