We were waiting several weeks to setting this contest and hope the problem was good enough.
Events
There was a difficulty with 805E - Ice cream coloring/804C - Ice cream coloring. A little bug in the checker fortunately yields accepting an incorrect solution of only one person during the contest. I should apologize all of you because of this.
For this sentence, Vertices which have the i-th (1 ≤ i ≤ m) type of ice cream form a connected subgraph. You can find the meaning of "connected subgraph" with connected and subgraph, thus it can be empty as it is more logical. How ever, I should apologize all of the participants because of weak sample tests in the statement.
I will write the full editorial in the few next days, now some hints and short solutions exist here.
Hints
Almost half of numbers are divisible by two.
For the string shouldn't be any i ≤ n - 2, si = si + 2. Make some examples of little sizes.
805C - Find Amir / 804A - Find Amir
Find minimum weighted edges.
There is some edges with weight 0, try to connect them in a carefully way.
805D - Minimum number of steps / 804B - Minimum number of steps
The last situation is some 'a' characters after some 'b' ones.
The last situation is unique.
The number of steps is also unique.
Each 'b' character makes a number of 'b' characters in the last situation according to the number of 'a' characters before it.
805E - Ice cream coloring / 804C - Ice cream coloring
We want to color the ice creams in a way that all of ice creams in a vertex would be different with this condition that if two vertices u and v have ice cream i, then all of vertices in the unique path of u and v would have it.
Let's have a trivial lower-bound for the answer.
The trivial lower-bound should be maximum size of vertices' sets.
You can prove that by induction on leaves of the tree. And code it how you proved it.
805F - Expected diameter of a tree / 804D - Expected diameter of a tree
Let's solve the problem for just two tree.
dt is diameter of t-th tree and fi is the maximum path starting from vertex i, for all valid i and j, assume that the edge is between them and find the diameter with max(fi + fj + 1, max(d1, d2)).
consider this trivial 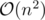 solution and try to improve it to
solution and try to improve it to 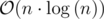 .
.
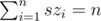
seems SQRT.
For every new query, try to do it with the complexity of 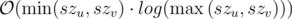 , which szi means size of the components of i-th vertex. Prove its complexity is
, which szi means size of the components of i-th vertex. Prove its complexity is 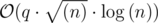 .
.
You can prove, we need even number of swaps to reach the same permutation. So 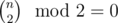 and the answer for 4·k + 3 and 4·k + 4 is -1.
and the answer for 4·k + 3 and 4·k + 4 is -1.
The solution almost is constructive.
And then solve n = 8 by n = 4.
Let's partition n = 4·k numbers to classes, each class contains a 4 consecutive numbers. And when n = 4·k + 1 there is a class with 5 consecutive numbers.
The problem consists two parts, the first part is to find mni and mxi, the minimum and the maximum score i-th vertex may get after the score distribution. The second part is to finding the answer and all your need to solve this part is those two arrays. It is trivial mni is number of real bullion of golds in i-th vertex.
Let's find the scores for two vertices u and v, u have a directed edge to v.
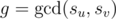
If i-th element from u-th vertex was painted and j-th element from v-th vertex was unpainted such that 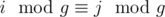 then j-th element from v-th vertex will be painted quickly. For two vertex, we can do it in complexity
then j-th element from v-th vertex will be painted quickly. For two vertex, we can do it in complexity 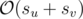 .
.
If we have this directed walk {w1, w2, ..., wk}, you should affect v1 on vk how I said in the previous hint with 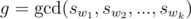 .
.
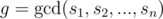
In this components if i-th element from u-th vertex was painted then for all of j such that 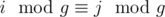 , j-th element from all vertices will be painted quickly. For this components, we can do it with complexity
, j-th element from all vertices will be painted quickly. For this components, we can do it with complexity 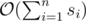 . In the main problem, we can suppose all of a strongly conected component a vertex with size g in this way and we can calculate mxi with answer of its component's vertex multiplied by
. In the main problem, we can suppose all of a strongly conected component a vertex with size g in this way and we can calculate mxi with answer of its component's vertex multiplied by 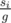 .
.
SCC of the tournament yields a Hamiltonian path of strongly connected components( if we consider each component a vertex ). The problem decreased to solve this path. we can solve the path with the complexity of sum of vertices' sizes.
Now, for every vertex we have minimum and maximum score it may get. For B known vertices, to check if they can be the wanted set, we can assume their score be maximum possible and the other scores be minimum possible. If they were top, then they can be a sample of the wanted set.
Consider a sorted sequence of combination of two array mn and mx.
For every vertex, consider the number of ways it(with its maximum score) can be the minimum score of the set of B vertices.
Solutions
Time Complexity: 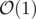
Memory complexity: 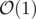
l,r=list(map(int,input().split()))
print(2 if l<r else l)
int main(){
int l, r;
scanf("%d%d", &l, &r);
printf("%d", l == r ? l : 2);
}
Time Complexity: 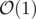
Time Complexity: 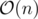
Memory complexity: 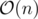
print(("aabb" * 50000)[:int(input())])
int N;
int main()
{
scanf("%d", &N);
for (int i = 0; i < N; i++)
putchar(i & 2 ? 'b' : 'a');
puts("");
}
Time Complexity: 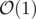
Time Complexity: 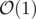
Memory complexity: 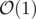
print((int(input())-1)//2)
int main(){
int n;
scanf("%d", &n);
printf("%d\n", (n-1)/2);
}
From: MohammadJA, Writer: MohammadJA
Time Complexity: 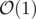
Time Complexity: 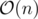
Memory complexity: 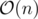
s = input()
cnt = 0
m=10**9 + 7
t = 0
for i in range(len(s)):
if s[~i] == 'a':
cnt = (cnt+t)%m
t = (t*2)%m
else:
t += 1
print(cnt)
int c,d,i,n,m,k,x,j=1000000007;
string s;
main(){
cin>>s;
for(i=s.size()-1;i>=0;i--){
if(s[i]=='b')c++;else{
k+=c;c*=2;k%=j;c%=j;
}
}
cout<<k;
}
Time Complexity: 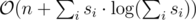
Memory complexity: 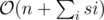
// +-- -- --++-- +-In the name of ALLAH-+ --++-- -- --+ \\
int const N = 3e5 + 10 ;
int n , m , ans = 1 , res[N] ;
vector <int> g[N] , vec[N] ;
inline bool cmp (int a , int b) {
return res[a] < res[b] ;
}
void dfs (int v , int par = -1) {
int col = ans , p = (int)vec[v].size() - 1 ;
sort(vec[v].begin() , vec[v].end() , cmp) ;
for (int x : vec[v]) {
if (res[x]) {
continue ;
}
while (p >= 0 && col == res[vec[v][p]]) {
col -- ;
p -- ;
}
res[x] = col ;
col -- ;
}
for (int u : g[v]) {
if (u != par) {
dfs(u , v) ;
}
}
}
int main(){
ios::sync_with_stdio(false) , cin.tie(0) , cout.tie(0) ;
cin >> n >> m ;
for (int i = 0 ; i < n ; i ++) {
int sz ;
cin >> sz ;
ans = max(ans , sz) ;
while (sz --) {
int x ;
cin >> x ;
x -- ;
vec[i].push_back(x) ;
}
}
for (int i = 0 ; i < n - 1 ; i ++) {
int u , v ;
cin >> u >> v ;
u -- , v -- ;
g[u].push_back(v) ;
g[v].push_back(u) ;
}
dfs(0) ;
cout << ans << '\n' ;
for (int i = 0 ; i < m ; i ++) {
cout << max(res[i] , 1) << ' ' ;
}
cout << '\n' ;
}
Time Complexity: 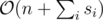
Memory complexity: 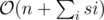
vector <int> Vs[300050];
vector <int> conn[300050];
int ans[300050];
bool chk[500050];
bool dchk[300050];
vector <int> Vu;
void DFS(int n) {
dchk[n] = true;
for (auto it : Vs[n]) {
if (ans[it]) chk[ans[it]] = true;
else Vu.push_back(it);
}
int a = 1;
for (auto it : Vu) {
while (chk[a]) a++;
ans[it] = a++;
}
for (auto it : Vs[n]) chk[ans[it]] = false;
Vu.clear();
for (auto it : conn[n]) {
if (dchk[it]) continue;
DFS(it);
}
}
int main() {
int N, M, i;
scanf("%d %d", &N, &M);
for (i = 1; i <= N; i++) {
int t1, t2;
scanf("%d", &t1);
while (t1--) {
scanf("%d", &t2);
Vs[i].push_back(t2);
}
}
for (i = 1; i < N; i++) {
int t1, t2;
scanf("%d %d", &t1, &t2);
conn[t1].push_back(t2);
conn[t2].push_back(t1);
}
DFS(1);
int mx = 0;
for (i = 1; i <= M; i++) {
mx = max(mx, ans[i]);
if (ans[i] == 0) ans[i] = 1;
}
mx = max(mx, 1);
printf("%d\n", mx);
for (i = 1; i <= M; i++) printf("%d ", ans[i]);
return !printf("\n");
}
From: MohammadJA, Writer: MohammadJA
Time Complexity: 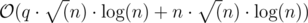
Memory complexity: 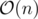
using namespace std ;
#define int long long
const int MAXN = 1e5 + 100 ;
vector<int>ver[MAXN] , com[MAXN] , ps[MAXN] ;
int vis[MAXN] , dis[MAXN] ;
int mxr , mxid ;
void dfs(int v , int col = -1 , int h = 0 , int par = -1){
vis[v] = max(vis[v] , col) ;
if(mxr < h)mxid = v , mxr = h ;
dis[v] = max(h , dis[v]) ;
if(col > 0)com[col] . push_back(dis[v]) ;
for(auto u : ver[v]){
if(u == par)continue ;
dfs(u , col , h + 1 , v) ;
}
}
map<pair<int , int> , int> check ;
int32_t main(){
ios_base::sync_with_stdio(0) ;
cin . tie(0) ; cout . tie(0) ;
int n , m , q ; cin >> n >> m >> q ;
for(int i = 0 ; i < m ; i ++){
int x , y ; cin >> x >> y ;
x -- , y -- ;
ver[x] . push_back(y) ;
ver[y] . push_back(x) ;
}
int cnt = 0 ;
for(int i = 0 ; i < n ; i ++){
if(vis[i])continue ;
mxr = 0 , mxid = i ;
dfs(i) ;
mxr = 0 ;
dfs(mxid) ;
dfs(mxid , ++ cnt) ; sort(com[cnt] . begin() , com[cnt] . end()) ;
ps[cnt] . push_back(0) ;
for(auto v : com[cnt])ps[cnt] . push_back(ps[cnt] . back() + v) ;
}
cout << fixed << setprecision(10) ;
while(q --){
int x , y ; cin >> x >> y ;
x -- , y -- ; x = vis[x] ; y = vis[y] ;
if(com[x] . size() > com[y] . size())swap(x , y) ;
if(x == y){cout << -1 << '\n' ; continue ; }
if(check[{x , y}] > 0){cout << double(check[{x , y}]) / (1ll * com[x] . size() * com[y] . size()) << '\n' ; continue ; }
int ans = 0 , mxd = max(com[x] . back() , com[y] . back()) ;
for(auto v : com[x]){
int num = lower_bound(com[y] . begin() , com[y] . end() , mxd - v - 1) - com[y] . begin() ;
ans += num * mxd + (com[y] . size() - num) * (v + 1) + ps[y] . back() - ps[y][num] ;
}
check[{x , y}] = ans ;
cout << double(check[{x , y}]) / (1ll * com[x] . size() * com[y] . size()) << '\n' ;
}
}
Time Complexity: 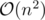
Memory complexity: 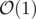
int n;
int main()
{
scanf("%d",&n);
if(n%4>1)return printf("NO\n"),0;
printf("YES\n");
for(int i=1;i<n;i+=4)
{
if(n%4)printf("%d %d\n%d %d\n%d %d\n",i+2,n,i+2,i+3,i+3,n);
else printf("%d %d\n",i+2,i+3);
printf("%d %d\n",i,i+2);
printf("%d %d\n",i+1,i+3);
printf("%d %d\n",i+1,i+2);
printf("%d %d\n",i,i+3);
if(n%4)printf("%d %d\n%d %d\n%d %d\n",i,n,i,i+1,i+1,n);
else printf("%d %d\n",i,i+1);
}
for(int i=1;i<n;i+=4)
for(int j=i+4;j<n;j+=4)
{
printf("%d %d\n",i+3,j+2);
printf("%d %d\n",i+2,j+2);
printf("%d %d\n",i+3,j+1);
printf("%d %d\n",i,j+1);
printf("%d %d\n",i+1,j+3);
printf("%d %d\n",i+2,j+3);
printf("%d %d\n",i+1,j+2);
printf("%d %d\n",i+1,j+1);
printf("%d %d\n",i+3,j);
printf("%d %d\n",i+3,j+3);
printf("%d %d\n",i,j+2);
printf("%d %d\n",i,j+3);
printf("%d %d\n",i+2,j);
printf("%d %d\n",i+2,j+1);
printf("%d %d\n",i+1,j);
printf("%d %d\n",i,j);
}
return 0;
}
Time Complexity: 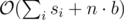
Memory complexity: 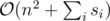
import java.io.OutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.io.BufferedWriter;
import java.util.InputMismatchException;
import java.io.IOException;
import java.util.Stack;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
import java.util.Vector;
import java.io.Writer;
import java.io.OutputStreamWriter;
import java.util.BitSet;
import java.io.InputStream;
/**
* Built using CHelper plug-in
* Actual solution is at the top
*/
public class Main {
public static void main(String[] args) {
InputStream inputStream = System.in;
OutputStream outputStream = System.out;
InputReader in = new InputReader(inputStream);
OutputWriter out = new OutputWriter(outputStream);
TaskF solver = new TaskF();
solver.solve(1, in, out);
out.close();
}
static class TaskF {
public int mod = 1000000007;
public int n;
public int a;
public int b;
public char[][] adj;
public List<Integer>[] graph;
public void solve(int testNumber, InputReader in, OutputWriter out) {
n = in.nextInt();
a = in.nextInt();
b = in.nextInt();
adj = new char[n][n];
graph = Stream.generate(ArrayList::new).limit(n).toArray(List[]::new);
for (int i = 0; i < n; i++) adj[i] = in.next().toCharArray();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (adj[i][j] == '1') {
graph[i].add(j);
}
}
}
List<List<Integer>> comp = new SCCTarjan().scc(graph);
boolean[][] can = new boolean[n][];
int[] low = new int[n];
for (int i = 0; i < n; i++) {
int q = in.nextInt();
char[] w = in.next().toCharArray();
can[i] = new boolean[q];
for (int j = 0; j < q; j++) {
can[i][j] = w[j] == '1';
if (can[i][j]) low[i]++;
}
}
int[] wcomp = new int[n];
int idx = 0;
List<BitSet> bb = new ArrayList<>();
List<Integer> bs = new ArrayList<>();
for (List<Integer> gg : comp) {
int gcd = 0;
for (int x : gg) {
gcd = Utils.gcd(gcd, can[x].length);
wcomp[x] = idx;
}
idx++;
BitSet d = new BitSet(gcd);
bs.add(gcd);
bb.add(d);
for (int x : gg) {
for (int i = 0; i < can[x].length; i++) {
if (can[x][i]) {
d.set(i % gcd, true);
}
}
}
}
for (int kk = comp.size() - 1; kk > 0; kk--) {
int g = Utils.gcd(bs.get(kk), bs.get(kk - 1));
BitSet ww = new BitSet(g);
for (int i = 0; i < bs.get(kk); i += g) {
ww.or(bb.get(kk).get(i, i + g));
}
for (int i = 0; i < bs.get(kk - 1); i++) {
if (ww.get(i % g)) {
bb.get(kk - 1).set(i, true);
}
}
}
int[] high = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < can[i].length; j++) {
if (bb.get(wcomp[i]).get(j % bs.get(wcomp[i])))
high[i]++;
}
}
long ret = 0;
int[][] comb = Utils.getComb(n + 1, mod);
for (int lowest = 0; lowest < n; lowest++) {
int countabove = 0;
for (int other = 0; other < n; other++) {
if (other == lowest) continue;
if (low[other] > high[lowest]) {
countabove++;
}
}
if (countabove >= a) {
continue;
}
int canbig = 0;
for (int other = 0; other < n; other++) {
if (other == lowest) continue;
if (low[other] <= high[lowest] && (high[other] > high[lowest] || (high[other] == high[lowest] && other > lowest))) {
canbig++;
}
}
for (int take = 0; take < b && take <= canbig && take + countabove < a; take++) {
ret = (ret + 1L * comb[canbig][take] * comb[countabove][b - take - 1]) % mod;
}
}
out.println(ret);
}
}
static class OutputWriter {
private final PrintWriter writer;
public OutputWriter(OutputStream outputStream) {
writer = new PrintWriter(new BufferedWriter(new OutputStreamWriter(outputStream)));
}
public OutputWriter(Writer writer) {
this.writer = new PrintWriter(writer);
}
public void close() {
writer.close();
}
public void println(long i) {
writer.println(i);
}
}
static class Utils {
public static int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
public static int[][] getComb(int sz, int mod) {
int[][] comb = new int[sz][sz];
for (int i = 0; i < sz; i++) {
comb[i][0] = 1;
for (int j = 1; j <= i; j++) {
comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
if (comb[i][j] >= mod) comb[i][j] -= mod;
}
}
return comb;
}
}
static class InputReader {
private InputStream stream;
private byte[] buf = new byte[1024];
private int curChar;
private int numChars;
public InputReader(InputStream stream) {
this.stream = stream;
}
public int read() {
if (this.numChars == -1) {
throw new InputMismatchException();
} else {
if (this.curChar >= this.numChars) {
this.curChar = 0;
try {
this.numChars = this.stream.read(this.buf);
} catch (IOException var2) {
throw new InputMismatchException();
}
if (this.numChars <= 0) {
return -1;
}
}
return this.buf[this.curChar++];
}
}
public int nextInt() {
int c;
for (c = this.read(); isSpaceChar(c); c = this.read()) {
;
}
byte sgn = 1;
if (c == 45) {
sgn = -1;
c = this.read();
}
int res = 0;
while (c >= 48 && c <= 57) {
res *= 10;
res += c - 48;
c = this.read();
if (isSpaceChar(c)) {
return res * sgn;
}
}
throw new InputMismatchException();
}
public String next() {
int c;
while (isSpaceChar(c = this.read())) {
;
}
StringBuilder result = new StringBuilder();
result.appendCodePoint(c);
while (!isSpaceChar(c = this.read())) {
result.appendCodePoint(c);
}
return result.toString();
}
public static boolean isSpaceChar(int c) {
return c == 32 || c == 10 || c == 13 || c == 9 || c == -1;
}
}
static class SCCTarjan {
List<Integer>[] graph;
boolean[] visited;
Stack<Integer> stack;
int time;
int[] lowlink;
List<List<Integer>> components;
public List<List<Integer>> scc(List<Integer>[] graph) {
int n = graph.length;
this.graph = graph;
visited = new boolean[n];
stack = new Stack<>();
time = 0;
lowlink = new int[n];
components = new ArrayList<>();
for (int u = 0; u < n; u++)
if (!visited[u])
dfs(u);
return components;
}
void dfs(int u) {
lowlink[u] = time++;
visited[u] = true;
stack.add(u);
boolean isComponentRoot = true;
for (int v : graph[u]) {
if (!visited[v])
dfs(v);
if (lowlink[u] > lowlink[v]) {
lowlink[u] = lowlink[v];
isComponentRoot = false;
}
}
if (isComponentRoot) {
List<Integer> component = new ArrayList<>();
while (true) {
int x = stack.pop();
component.add(x);
lowlink[x] = Integer.MAX_VALUE;
if (x == u)
break;
}
components.add(component);
}
}
}
}
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
const int maxn = 5005;
const int maxelem = 2000006;
const int MOD = 1000000007;
char gr[maxn][maxn];
string init[maxn];
int mincnt[maxn], maxcnt[maxn];
int c[maxn][maxn];
int n, m, A, B;
bool was[maxn];
vector<int> order;
vector<bool> can[maxn];
bool nowcan[maxelem];
char s[maxelem];
int gcd[maxn];
vector<int> comp[maxn];
void preorder(int cur)
{
if (was[cur]) return;
was[cur] = true;
for (int i = 0; i < n; i++) if (gr[cur][i] == '1') preorder(i);
order.pb(cur);
}
void color(int cur, int cc)
{
if (was[cur]) return;
was[cur] = true;
gcd[cc] = __gcd(gcd[cc], (int)init[cur].size());
comp[cc].pb(cur);
for (int i = 0; i < n; i++) if (gr[i][cur] == '1') color(i, cc);
}
int getc(int n, int k)
{
if (k < 0 || k > n) return 0;
return c[n][k];
}
int main()
{
scanf("%d%d%d", &n, &A, &B);
for (int i = 0; i < n; i++)
{
scanf("%s", gr[i]);
}
for (int i = 0; i < n; i++)
{
scanf("%*d");
scanf("%s", s);
init[i] = string(s);
for (int j = 0; j < (int)init[i].size(); j++) mincnt[i] += init[i][j] == '1';
maxcnt[i] = mincnt[i];
}
for (int i = 0; i < n; i++) if (!was[i]) preorder(i);
memset(was, 0, sizeof(was));
int cc = 0;
reverse(all(order));
for (auto t : order) if (!was[t])
{
color(t, cc);
cc++;
}
for (int i = 0; i < cc; i++)
{
can[i].resize(gcd[i]);
for (int j = 0; j < gcd[i]; j++) can[i][j] = false;
for (auto t : comp[i])
{
for (int j = 0; j < (int)init[t].size(); j++) if (init[t][j] == '1') can[i][j % gcd[i]] = true;
}
}
for (int i = 0; i < cc - 1; i++)
{
int g = __gcd(gcd[i], gcd[i + 1]);
for (int j = 0; j < g; j++) nowcan[j] = false;
for (int j = 0; j < gcd[i]; j++) nowcan[j % g] |= can[i][j];
for (int j = 0; j < gcd[i + 1]; j++) can[i + 1][j] = (can[i + 1][j] | nowcan[j % g]);
}
for (int i = 0; i < cc; i++)
{
for (auto t : comp[i])
{
for (int j = 0; j < (int)init[t].size(); j++) if (init[t][j] == '0' && can[i][j % gcd[i]]) maxcnt[t]++;
}
}
c[0][0] = 1;
for (int i = 1; i <= n; i++)
{
c[i][0] = 1;
for (int j = 1; j <= i; j++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % MOD;
}
int answer = 0;
for (int i = 0; i < n; i++)
{
int cntbigger = 0;
int cntupper = 0;
for (int j = 0; j < n; j++) if (i != j)
{
if (mincnt[j] > maxcnt[i]) cntbigger++;
else if (maxcnt[j] > maxcnt[i] || (maxcnt[j] == maxcnt[i] && j > i)) cntupper++;
}
if (cntbigger >= A) continue;
for (int j = max(0, B - 1 - cntbigger); j <= cntupper && j + cntbigger + 1 <= A && j + 1 <= B; j++)
{
answer = (answer + (ll)getc(cntupper, j) * getc(cntbigger, B - 1 - j)) % MOD;
}
}
cout << answer << endl;
return 0;
}
#include <bits/stdc++.h>
#define xx first
#define yy second
#define mp make_pair
#define pb push_back
#define fill( x, y ) memset( x, y, sizeof x )
#define copy( x, y ) memcpy( x, y, sizeof x )
using namespace std;
typedef long long LL;
typedef pair < int, int > pa;
inline int read()
{
int sc = 0, f = 1; char ch = getchar();
while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1; ch = getchar(); }
while( ch >= '0' && ch <= '9' ) sc = sc * 10 + ch - '0', ch = getchar();
return sc * f;
}
const int MAXN = 5005;
const int MAXM = 2000005;
const int mod = 1e9 + 7;
int n, a, b, len[MAXN], can[MAXM], id_cnt, L[MAXN], R[MAXN], C[MAXN][MAXN];
int dfn[MAXN], scc[MAXN], low[MAXN], tim, num, st[MAXN], top, w[MAXN], ans;
vector < int > G[MAXN], id[MAXN], scc_bit[MAXN], v[MAXN];
char ch[MAXM];
inline void inc(int &x, int y) { x += y; if( x >= mod ) x -= mod; }
inline void dfs(int x)
{
dfn[ x ] = low[ x ] = ++tim; st[ ++top ] = x;
for( auto y : G[ x ] )
if( !dfn[ y ] ) dfs( y ), low[ x ] = min( low[ x ], low[ y ] );
else if( !scc[ y ] ) low[ x ] = min( low[ x ], dfn[ y ] );
if( dfn[ x ] == low[ x ] )
{
num++; int t = 0;
while( t ^ x )
{
scc[ t = st[ top-- ] ] = num;
w[ num ] = __gcd( w[ num ], len[ t ] );
v[ num ].pb( t );
}
scc_bit[ num ].resize( w[ num ] );
for( auto y : v[ num ] )
for( int d = 0 ; d < len[ y ] ; d++ ) if( can[ id[ y ][ d ] ] ) scc_bit[ num ][ d % w[ num ] ] = 1;
}
}
int main()
{
#ifdef wxh010910
freopen( "data.in", "r", stdin );
#endif
n = read(), a = read(), b = read();
for( int i = 0 ; i <= n ; i++ )
{
C[ i ][ 0 ] = 1;
for( int j = 1 ; j <= i ; j++ ) inc( C[ i ][ j ] = C[ i - 1 ][ j ], C[ i - 1 ][ j - 1 ] );
}
for( int i = 1 ; i <= n ; i++ )
{
scanf( "%s", ch + 1 );
for( int j = 1 ; j <= n ; j++ ) if( ch[ j ] == '1' ) G[ i ].pb( j );
}
for( int i = 1 ; i <= n ; i++ )
{
len[ i ] = read(); scanf( "%s", ch );
for( int j = 0 ; j < len[ i ] ; j++ ) id[ i ].pb( ++id_cnt ), can[ id_cnt ] = ch[ j ] == '1', L[ i ] += can[ id_cnt ];
}
for( int i = 1 ; i <= n ; i++ ) if( !dfn[ i ] ) dfs( i );
for( int i = num ; i > 1 ; i-- )
{
int g = __gcd( w[ i ], w[ i - 1 ] );
w[ i - 1 ] = g;
for( int j = 0 ; j < w[ i ] ; j++ ) scc_bit[ i - 1 ][ j % g ] |= scc_bit[ i ][ j ];
}
for( int i = 1 ; i <= n ; i++ )
{
int x = scc[ i ];
for( int j = 0 ; j < len[ i ] ; j++ )
R[ i ] += scc_bit[ x ][ j % w[ x ] ];
}
for( int i = 1 ; i <= n ; i++ )
{
int t1 = 0, t2 = 0;
for( int j = 1 ; j <= n ; j++ ) if( L[ j ] > R[ i ] ) t1++;
if( t1 >= a ) continue;
for( int j = 1 ; j <= n ; j++ ) if( L[ j ] <= R[ i ] && mp( R[ j ], j ) > mp( R[ i ], i ) ) t2++;
for( int j = 0 ; j < b && j <= t2 && j + t1 < a ; j++ )
inc( ans, 1LL * C[ t2 ][ j ] * C[ t1 ][ b - j - 1 ] % mod );
}
return printf( "%d\n", ans ), 0;
}
As my good friend, Arpa, did, let me share with you a perfect poem of one of our best poet you might know, Molavi:
.......................................................................................بند بگسل، باش آزاد ای پسر ** چند باشی بند سیم و بند زر
O son, burst thy chains and be free! How long wilt thou be a bondsman to silver and gold?
.......................................................................................گر بریزی بحر را در کوزهای ** چند گنجد قسمت یک روزهای
If thou pour the sea into a pitcher, how much will it hold? One day's store.
..................................................................................... کوزهی چشم حریصان پر نشد ** تا صدف قانع نشد پر در نشد
The pitcher, the eye of the covetous, never becomes full: the oyster - shell is not filled with pearls until it is contented.
.............................................................................. هر که را جامه ز عشقی چاک شد ** او ز حرص و عیب کلی پاک شد
He (alone) whose garment is rent by a (mighty) love is purged entirely of covetousness and defect.











Auto comment: topic has been updated by saliii (previous revision, new revision, compare).
If we had these types of editorials for future contest as well, could be good. Sometimes all you want is hints :)
I totally agree, this is what editorials here need.
It would be awesome to have hints after every contest, it's really all you might be missing to solve a problem(especially when you're upsolving).
Thanks saliii !
YW!
We were waiting several weeks to setting this contest and hope the problem was good enough.Why didn't you write full editorial for this several weeks?
we were trying different problems, there is near 4 or 5 really good problems, we don't use them here for different reasons. And we wrote a big part of editorial! To be honest, We started preparing the contest from 4 mouth ago.
In Div2 E /Div1 C , How to implement what is written in the editorial ??? I realized the hints during the contest but I really could not come up how to implement it efficiently ???
Do dfs from any vertex T and keep set of used colors in each vertex. When you come in some vertex try to set colors for each type in way like:
After you set a color for a type do another dfs from this vertex in every other vertex which have same type and insert this color in their used sets. Total complexity is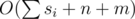 .
.
I do not understand
Vertices which have the i-th (1 ≤ i ≤ m) type of ice cream form a connected subgraphin problem. Form a connected subgraph of what graph and in which graph?? ignoring this forms G a forest like structure of cliques.tia
Forms connected subgraph in original tree. So all vertices with same type are connected by tree edges. For example 1 to 1,2 to 2 is ok, but 1 to 2 to 1,2 not okay (as 1 and 1,2 should be connected by edge to form connected subtree). It wasn't clear for me too.
thanks, i looked at your comments below, now clear why graph in your ex is invalid. so G will be a disconnected graph of cliques and hence min col is max size of a clique.
no i am not right. i'm being stupid.
nice contest
In Div1 C Editorial:
The trivial upper-bound should be maximum size of vertices sets.I think this is a trivial lower-bound of the answer, perhaps it is trivial as upper-bound too but in that case is trivial that this is the answer.
Thanks, edited.
can you please explain why is the upper bound max of vertices sets?
Okay, I understand why it's not nlogn.
Why All of my submissions show skipped? Though all of them are passed in system test.
This was my first contest, can anyone help me with Div2 D problem ? I am not able to figure out the logic from hints.
Thanks.
My approach: consider x letters 'a' in a row and a single letter 'b'. Try to figure out the required number of steps to turn this to (many letters b + x letters 'a') for an arbitrary x.
For example, x = 3 (x = 2 is given as a problem sample) aaab -> aabba -> abbaba -> bbababa -> bbbbaaba -> bbbbabbaa -> bbbbbbabaa -> bbbbbbbbaaa :)
can you pls elaborate more?? i tried but not able to follow.
Ok :) The fact that can be used to solve this one: should you have x letters 'a' and a single 'b', this will soon turn to a string of y letters 'b' and x letters 'a'. What's the value of y? :) As given in samples, aab will turn to bbbbaa.
i followed someone's solution sol and what it does is: iterate from right and find answer for index where a's are present and update number of b's right to this. is it not miscounting as in your above ex if we follow this pattern then in 4th step(bbbbaaba) leftmost a has to wait 1 more step to be interchanged. how is it compeseted overall??
Look this comment
The end of changes is string s like b....ba.....a, because you can't find substring ab.
Okey, let's try to do this string, as we can see when you meet ab it replace with bba, so a and b swap, but if we have aab it became abba, so we can find new ab and after two moves it becames bbbbaa and so on...
So, when we find new ab, it will not changes smth after it, just previous string, because of that we can iterate from left to right, count all a, and, when we find b, swap all found a with this b.
If you modulate this process, you see, that if you have n a before b you will make 1 + 2 + 4 + ... + 2n - 1 moves or 2n - 1.
And we got solution:
just use precalc or bin_pow with module
Ice coloring: Could someone explain how following given tree topology — colors it correctly? Which part of problem guarantees it?
For example not following tree, just processing by tree vertex index, would fail on test 143 that is a custom hack.
Did you understand why processing by tree vertex index is wrong?
I understand why it's wrong. But I don't understand why processing by tree edges is correct.
For example 2 3
1 1 1 2 2 1 2
1 2 2 3 Would fail when processing by tree edges, but why this input is incorrect?
Umm, is the input correct? I think the edges should be 1 3, 2 3 due to each icecream being in a connected subgraph.
Ok, thanks, now I understand that each type of ice cream must form connected subgraph in a tree.
I don't know why processing by tree vertex index is wrong though. I think there should always be enough colors to avoid clashes, which means it should work. Hopefully someone clarifies.
In 805F — Expected diameter of a tree, may I ask how to get the maximum path of each vertices in a graph? Is it run from a vertex to all vertices in its graph to get that vertex maximum path or is there a better way to do it? Thanks.
Prove me someone if I am wrong, but we can find center(es) of tree and half of diameter + distance to closest center is maximal distance
As I finding and try to learning from the provided solution, finding the diameter for each vertices in graph needed 3 times doing the dfs, the first one is finding the farthest vertex from a vertex (V), the second is calculate the diameter of the vertex from vertex V and also finding the farthest vertex again, and the third is to calculate the diameter from the other farthest vertex from second dfs. Is my understanding true? Thank you :)
In editorial, there is a code with 3 dfs! but I think we can do it by a simple dp_up down in 2 dfs maybe!
Ok. Thanks! :D
804E — The same permutation Hint 1: Should be 4*k + 2 instead of 4*k + 4.
Ok. Obviously stupid question, but still I don't know how to prove that: sum sz_i = n => sum min(sz_u, sz_v) log(max(sz_u, sz_y))=n sqrt(n) log(n)? I suppose, we should prove that sum min(sz_u, sz_u) <= n sqrt(n)... Thank you
.
Imagine you have a graph where each vertex represents one of the components and has weight equal to the size of that component. Your task is to draw n-1 edges weight of each is equal to minimum among vertexes it connects in order to maximize the total weight of edges. It's obvious that the worst case happens when you form a clique of x heaviest vertexes (such that (x — 1)x = 2n since multuedges aren't allowed). That gives you that each vertex has no more than sqrt(n) edges. That's it :)
As I didn't see anybody explaining the simple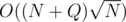 solution I decided to do so.
solution I decided to do so.
Well it's not exactly what you ask but I think you will understand my solution better (and it works in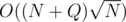 ). First you must be able to solve the problem for two trees in O(szu + szv) time. In the editorial there is a
). First you must be able to solve the problem for two trees in O(szu + szv) time. In the editorial there is a 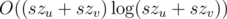 . If you do the one described in the editorial your solution will simply run in
. If you do the one described in the editorial your solution will simply run in 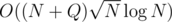 time.
time.
So now lets solve the other part of the problem. Lets consider 2 case:
1) For a query (u, v),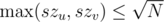 . For such queries we simply run the
. For such queries we simply run the 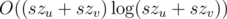 or O(szu + szv) solution. The overall complexity for such queries then will be
or O(szu + szv) solution. The overall complexity for such queries then will be 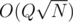 or
or 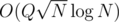 .
.
2) For a query (u, v),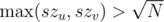 . Lets assume that szv ≤ szu. How many trees u such that
. Lets assume that szv ≤ szu. How many trees u such that 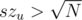 exist? Well you can simply prove that they are at most
exist? Well you can simply prove that they are at most 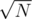 , because
, because 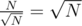 . Then we can precompute for every "heavy" tree u answer with every other tree v. For a fixed tree u this precompute will have complexity O(N) or
. Then we can precompute for every "heavy" tree u answer with every other tree v. For a fixed tree u this precompute will have complexity O(N) or  depending how you solve the problem for 2 trees. Then this part will be done in
depending how you solve the problem for 2 trees. Then this part will be done in 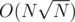 time (or
time (or 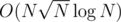 ) and will take
) and will take 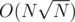 memory.
memory.
So then the whole solution will take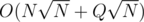 or
or 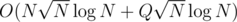 and
and 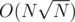 memory.
memory.
Here is my Accepted code: 26851219
PS: You can see a constant B which I use as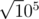 . Idk why during the contest I thought
. Idk why during the contest I thought 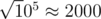 . It's actually about 315.
. It's actually about 315.
Separating big and small components is useful for analysis but in code you can just solve for each query separately and reuse the answer in case of duplicate queries
Oh nice. I actually thought about that during the contest but that the complexity seemed O(N * Q) to me. Now when I thought for a bit it actually is easily provable that the complexity will be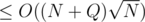 . Thanks for sharing :)
. Thanks for sharing :)
How do you solve two trees without log? You do still need to sort verticies with farthest distance from them, right? (And then two pointers)
Read your code and got it, thx.
We will use the following observations:
1) If we have a tree the furthest vertex away from any vertex u will be one of the two ends of any diameter of this tree. You can easily prove this. Let's define d(u) to be the maxiaml distance from vertex u to any other vertex in its tree. Using this observation we can find d(u) for every u in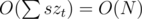 by preforming a couple of DFSes (first we find a diameter of the tree and the we do one DFS from both its ends).
by preforming a couple of DFSes (first we find a diameter of the tree and the we do one DFS from both its ends).
2) When we add the edge between the two trees we will have dimeter equal to max(diamT(u), diamT(v), d(u) + d(v) + 1). Let's define D = max(diamT(u), diamT(v)). Obviously we can solve the problem independently for one of the trees. By this I mean we pick one of the trees and then for every vertex of the other tree we get the expected diameter if we have chosen it as one of the ends of the edge we will add. Then we if that vertex is u we need to find the count of vertices v such that D > d(u) + d(v) + 1 because for them it is optimal to save our previous diameter. This inequality equivalent to D - d(u) - 1 > d(v). From right we have a constant. How can we find the number of vertices v satisfying the inequality? We can use partail sums. Same goes for the case when D ≤ d(u) + d(v) + 1 but there we do partial sums of d(v). You can reffer to my code.
805D-Minimum Number Of Steps what is wrong with this solution somebody help me.
take mod for : 1) no_b += no_b ; 2)no_b++
You get overflow in
no_bAuto comment: topic has been updated by saliii (previous revision, new revision, compare).
For Div1 C / Div2 E, would it be possible to get input data used for #17 ?
Hi, here is one question, for 804C Ice cream coloring. Will this algorithm work? During inputting tree T, record every pair of ice creams in every set of T's vertex as an edge of G. For example, if there are k ice creams in the set of a T's vertex, then we add k(k - 1) / 2 edges for G during its input(eliminating duplicates). After the construction of G, run a traditional colouring algorithm for it. Such solution doesn't use T as a tree and there is no dfs. But wrong at test case 3. I wondered what is wrong for the whole day:(
There might be O(n^2) edges on G, that doesn't fit memory/time. Edit: also, iirc coloring a general graph is np-complete (might be wrong).
me too have same problem. can't figure out what's the use of input tree T.
check this comment for detail.
Auto comment: topic has been updated by saliii (previous revision, new revision, compare).
I am getting TLE on test 25 for Div2 F/Div1 D. Can anyone tell what the problem is I can't seem to find it thanks in advance. Code : http://codeforces.net/contest/804/submission/26910532
Auto comment: topic has been updated by saliii (previous revision, new revision, compare).
Can anyone plzz explain me why my solution is wrong?? http://codeforces.net/contest/805/submission/26964381 actually it gives correct answer for test case#13 on my machine..
The calculation of
xb*(a[xa]-1)overflows ifintis 32-bit.A bit simpler solution for the problem 804E (DIV1E).
I want to ask some questions about Div1 F.I can't understand the last part that is calculating the ans knowing mincnt[i] and maxcnt[i].For every j(j+bigger+1<=A), your code adds C(upper,j)*C(bigger,b-1-j) to the ans.But j is the number of mxs that are bigger or equal to mx[j] while the problem said "if there are no more than a - 1 gangs with power strictly more than p".Then there may be some situations you do not calculate such as many mxs are equal then your j if not about the number of strictly more than p,but is about mxs that are bigger or equal.Can someone help me?Am I right?
right, fixed.
I have a question about Div1.F.
Look at this case:
As the whole graph is an SCC ,the mn and mx are:
if we set the score as follow:
then we can choose any 2 gangs from gang 1,3,4,5, so the answer should be 6.
But the std code gives 4.
I wonder if i understood the problem incorrectly.Thanks!
In the question A (fake np) the answer in the second example (which is 3) is different from the answer that is tested during compiling the program on the website , why did the author do such a thing??
both 2 and 3 are right answers
what should be the answer if l and r given is 26 and 27?.... acc. to me it should be 3 ..correct me If I m wrong?
2,3,9,13,26 and 27 are correct answers
but 27=3x3x3...and 26=2x13....so 3 occurs most times...so only 3 would not be the answer
dude
3 is written only once
oh...I got it..thanku
I think in solution of problem C, there was a kind of mistake (python)
(int(input())-1)//2 just '/' instead of "//" maybe
all is right, '//' means integer dividing
oh, ok , sorry
what would be the answer in question A ...if l and r given is 26 and 27... answer should not be equal to 3 instead of 2...correct me if I m wrong !!
Am I only one who doesn't understand div1C/div2E problem statement???