→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 4039 |
| 2 | tourist | 3841 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3590 |
| 5 | ecnerwala | 3542 |
| 6 | Benq | 3535 |
| 7 | orzdevinwang | 3526 |
| 8 | gamegame | 3477 |
| 9 | heuristica | 3357 |
| 10 | Radewoosh | 3355 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | atcoder_official | 160 |
| 3 | Um_nik | 160 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/22/2025 18:54:46 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











The basic idea is: For every i, it makes sense either not to swap A[i] and B[i] at all, or to swap them exactly once. So every choice of (non)-swaps for the whole pair of strings can be represented as some n-bit binary number (i-th digit is 1 IFF you want to swap A[i] and B[i]). Since n < 16, it is feasible to try out all 2n possible numbers (i. e. all possible choices of (non)-swaps) and calculate max(n(A'), n(B')) naively (for example, by using two sets of characters, one for A', one for B'). Time complexity of this solution is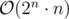 (possibly n + |Σ| for bigger alphabets).
(possibly n + |Σ| for bigger alphabets).
Hope I've been comprehensible enough.
I also suspect one can solve the task in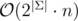 , but that's slower for our constraints anyway
, but that's slower for our constraints anyway
Actually if we see:
(2^16)*16*100 = 104857600 + some few operators ( which is greater than 10^8 computations for 1 s ( time complexity ), won't it time out.
100 is for test cases
Please helm me in this.
Oh, I forgot about the test cases...
Well, I'm not too sure about whether my solution would pass the 1s limit, but I think it could, since the actual running time depends a lot on what operations you perform. In this particular case, you just increment some numbers, do bitshifts and keep a 26-sized array (for counting distinct letters) which you can BTW replace with another bitmask (I'm not sure if it is actually faster or not). Since the memory complexity is nearly constant, I would say you are also kind to caches, which could help, too.
I think you could achive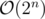 complexity by iterating over the bitmasks in a clever way (so there would be only one bit changed between two iterations), but personally, I would probably code the more naive solution and try to "prove by submit" first :-).
complexity by iterating over the bitmasks in a clever way (so there would be only one bit changed between two iterations), but personally, I would probably code the more naive solution and try to "prove by submit" first :-).
EDIT: I tried to implement the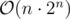 (more precisely,
(more precisely, 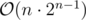 ) solution, it passed CF's custom invocation with t = 100, n = 16 in about 400 ms.
) solution, it passed CF's custom invocation with t = 100, n = 16 in about 400 ms.
EDIT 2: The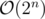 solution isn't as complicated as I expected. On the same test it runs for about 30 ms.
solution isn't as complicated as I expected. On the same test it runs for about 30 ms.
Could you share both of those solutions?
Okay (hope they are actually correct):
O(2^n)
O(2^n n)