yelghareeb's blog

Floating Point Precision
By yelghareeb, history, 7 years ago, In English

Hello Codeforces community,

In problem D (Area of Two Circles' Intersection), I wanted to calculate the angle between two vectors.

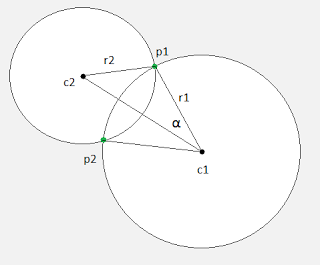
I calculated the angle α using the dot and cross products of the vectors c1p1 (name it V1) & c1c2 (name it V2) using the following equation:

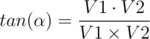
Then used the atan2 function to get the angle. I got a WA with a small precision drift in test 41. I changed the implementation to what was described in the editorial and calculated α using the low of cosines as follows:

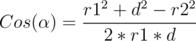
where d is the distance between the centers of the circles. I used the acos function to get the angle, this passed the system tests.Those are the links of my submissions:

Wrong: http://codeforces.net/contest/600/submission/27546617
Correct: http://codeforces.net/contest/600/submission/27546673

I wonder why my first approach failed.

Another problem, Nearest Vectors:
You are given the set of vectors on the plane, each of them starting at the origin. Your task is to find a pair of vectors with the minimal non-oriented angle between them.

I sorted the vectors w.r.t their angles, then looped on them minimizing the value of angle[i + 1] — angle[i]. I wrote the following function to get the angle between each vector and the positive direction of the X-Axis

long double get_ang(pii coords) {  
  double res = atan2(coords.second, coords.first);  
  if (res < 0) res += 2 * PI;  
  return res;  
}

This gave me WA in a test case 140, where 2 answers were very close in the difference. I modified the function and converted the angles to degrees and it passed. 

long double get_ang(pii coords) {  
  double res = atan2(coords.second, coords.first) * 180 / PI;  
  if (res < 0) res += 2 * PI;  
  return res;  
}

Wrong submission: http://codeforces.net/contest/598/submission/27534014
Correct submission: http://codeforces.net/contest/598/submission/27534469

I also wonder how this very slight modification affected the differences between angles.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

For the first problem, test 41 are one large circle and one small circle. In the first approach, calculating V1 cross V2 involves a subtraction of two near values, which will result in a lot of precision lost (and the division will magnify the error).

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

There is a stable version of Heron's formula, due to Kahan, at https://people.eecs.berkeley.edu/~wkahan/Triangle.pdf Have you considered using that for D? It's a very general idea, finding the area/angle of a possibly very thin triangle, and Heron's formula (the numerically stable version of it) is a nice primitive operation for it.

→ Reply