| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Hello.
Recently, I was solving a problem to which I simplified it to evaluating this summation:
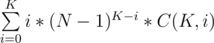
C is n choose k. N is up to 1000, and K is up to 2^30.
Answer appears to be I guess {K * (N - 1)K}
I can't get however how to arrive at this, or perhaps compute the original summation in a smart way, I tried messing expanding nCk to factorials, but didn't get anywhere. <.<
Hi. Do you have to modulo the answer by some prime number?
Modulo any number from 1 to 10^5 range.
Answer should be K·NK - 1.
You can see it like this: For all sequences constisting of 0 and 1 we sum number of ones multiplied by (N - 1)zeroes. It is equal to sum for all sequences for all ones (N - 1)zeroes. Then group summands by index of 1. We will get Sum for all positions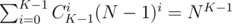
.
Nice solution. Thanks !
If someone else searches this in future or interested, there is also another way to look at it : Imagine K loops each from 1 to n, and in the final one you pick the K items your indices chose from N. It's equivalent to the summation. There will be K*N^K values picked in total, so you can see each element will contribute (K * NK) / N times.
The answer is K·NK - 1.
The last equality follows from the binomial theorem.
I initially could arrive at the second equation but didn't figure out the third simplification, do you mind explaining how did you move from the second one to the third? Maybe it's easy but I don't seem to see it. :(
Thanks!
Just expand the formula for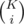
and simplify. Alternatively, there's a combinatorial explanation. We count the number of ways to choose a team of i people from K and choose a observer from the rest K - i.
Answer 1: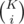
ways to choose the team. K - i to choose the observer. The answer is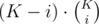 
Answer 2: This time we choose the observer first. He can be chosen K ways. The team can be chosen from the rest K - 1 in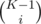
ways. The answer is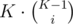 
Great!
Thanks again.