rachitiitr's blog

Introduction to New Data Structure: Wavelet Trees
By rachitiitr, history, 7 years ago, In English

Hi CF Community,

http://rachitiitr.blogspot.in/2017/06/wavelet-trees-wavelet-trees-editorial.html

I think it's safe to assume that this is a new data structure for most of us.
Consider the following problems:
1. Number of elements in subarray A[L...R] that are less than or equal to y.
(Persistence Segment Tree? Ordered multiset + BIT ?)
2. Number of occurrences of element x in subarray A[L...R].
(Subpart of 1st problem)
3. The kth smallest element in subarray A[L...R].
(Ordered multiset + BIT would work for subarrays beginning from index 1)

I know you might have many other solutions, and you might think what I am trying to prove.

What if I told you, all of the above can be easily done in O(logn) using Wavelet Trees :o. Plus, its very easy to code :D Awesome, isn't it?

Check the implementation here.

The post just introduces the basic usage of wavelet trees. There is still more that you can do with them.
I will write about them later, once I gain enough sleep maybe?

  • Vote: I like it
  • +256
  • Vote: I do not like it

Comments Comments (48)
| Write comment?
»
7 years ago, # |
  Vote: I like it +6 Vote: I do not like it

What about "change an element" queries? If we solve the problem offline, they can be reduced to two "toggle" queries. But is it possible to solve it online? For example, by using order statistic tree instead of BIT?

Also can someone explain why this structure is called a "wavelet tree"?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Wikipedia:

    The name derives from an analogy with the wavelet transform for signals, which recursively decomposes a signal into low-frequency and high-frequency components.

    → Reply
»
7 years ago, # |
  Vote: I like it +51 Vote: I do not like it

Author sleeping since 32 hours

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +17 Vote: I do not like it

    Lol, I have just graduated from college and started off with a new job in a new place. So, I am busy with the new life and searching for flats which is tiring af.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Very nice blog post.

But I would like to add 1 and 2 can be done in O(logn) using regular segment tree if queries can be handled offline(and no updates).

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Maybe I can't get how the first problem can be solved using segment tree offline,could you please explain it in detail? Thanks!

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Keep 2 kinds of queries:
      1. (x,i) : The ith position is supposed to be assigned value x
      2. (x,l,r): Count number of elements in [l,r] which are less than x

      So obviously the queries are of the form (a[i],i) for i from 1 to n, and the range queries that we have. Now sort all the queries by x. Keep a segment tree over 1 to n. Initially, all the nodes have the value 0. Now whenever you encounter the first query, set the value at i to 1. For the second query the answer is just the number of 1's from l to r, which is a normal range sum query.

      You can see pretty easily that this works.

      → Reply
»
7 years ago, # |
  Vote: I like it +73 Vote: I do not like it

Is it correct that wavelet tree is conceptually just a merge-sort-like-tree built on top of values instead of positions?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Not sure what you mean, but probably not. Haven't you mixed up "values" and "positions"?

    Wavelet tree was designed to overcome binary alphabet size limitation of succinct bit-vectors with constant-time rank and select queries. Thus the essence of wavelet trees is splitting the sequence over alphabet into series of bit-vectors in a balanced way. It certainly doesn't merge nor sorts anything.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      No, I did not.

      By "merge-sort-like-tree" I mean the following: suppose we have a standard segment tree over an array, but each node stores (instead of a fixed-size value) a sorted list of all values in the corresponding subtree. Here is an example for array 4 6 2 1 7 3 8 5:

      [1  2  3  4  5  6  7  8] - values on positions 1-8 (node 1)
[1  2  4  6][3  5  7  8] - values on positions 1-4, 5-8 (nodes 2 and 3)
[4  6][1  2][3  7][5  8] - values on positions 1-2, 3-4, 5-6, 7-8 (nodes 4-7)
[4][6][2][1][7][3][8][5] - values on positions 1, 2, ..., 8 (nodes 8-15)

      That data structure can easily calculate number of elements less than X whose positions are between L and R in — just split [L;R] into nodes and run binary search inside each node. With fractional cascading we can reduce that time into by running binary search on the top level only.

      Wavelet tree does something similar: instead of looking at values

      (1, 4); (2, 6); (3, 2); (4, 1); (5, 7); (6, 3); (7, 8); (8, 5)

      it looks at

      (4, 1); (6, 2); (2, 3); (1, 4); (7, 5); (3, 6); (8, 7); (5, 8)
similar to
(1, 4); (2, 3); (3, 6); (4, 1); (5, 8); (6, 2); (7, 5); (8, 7)

      and builds something similar to the structure we had above: each node corresponds to a sub-segment of possible values and contains their sorted positions (we have no need to store the positions explicitly, we just pretend that they're here):

      [1  2  3  4  5  6  7  8] - positions of values 1-8 (node 1)
[1  3  4  6][2  5  7  8] - positions of values 1-4, 5-8 (nodes 2-3)
[3  4][1  6][2  8][5  7] - positions of values 1-2, 3-4, 5-6, 7-8 (nodes 4-7)
[4][3][6][1][8][2][5][7] - positions of values 1, 2, ..., 8 (nodes 8-15)
      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Seems like one could say that these data structures are transposed versions of each other.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Having come up with another solution to your three problems,we can use a persistent segment tree to deal with all three problems online(We can deal with 1 and 2 directly,and for problem 3,we can do binary search on the persistent segment tree which is still O(logn)).So we can have an alternative way to solve your three problems in O(nlogn) memory and time complexity.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you explain how binary search on segment tree would be O(logn)?

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Are you considering updates as well?

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I haven't figured out how to do the "toogle" update with persistent segment tree — you have to actually update linear number of versions.

    Also, persistent segment tree is not, more strictly speaking, — it's 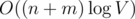memory and time, where n is the length of the array, m is the number of queries and V is the maximal value. By adding garbage collection we can reduce memory consumption to 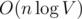, but that makes code harder (and if you use standard pointer like shared_ptr it significantly increases hidden const).

    On the other hand, wavelet tree takes memory without garbage collection and 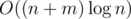time.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      If we can compress values, persistent segment tree is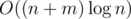 . If we can't, wavelet tree is also .

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

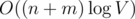        Fair enough. Is there any situation where we cannot compress values, but can build wavelet tree?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          For example, if we need to process online "push_back" updates.

          → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I didn't mean persistent segment tree is better than wavelet tree,and wavelet tree certainly does better in these kind of problems.I just point out that there exists an alternative way to solve these kind of problems.

      What's more,if we are asked to update values and even insert new values,we can use binary search tree without rotations(In China it's called Scape-Goat Tree) and segment tree to solve the problem in O(nlog^2n) time complexity.

      There is a problem of this kind which you're asked to ask queries of the k-th smallest element in a range as well as update and insert elements.

      Problem Link(in Chinese)

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        Would you mind elaborating what is Scape-Goat tree a little? Is it like segment tree for 109 leaves with dynamically allocated nodes?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          Scape-Goat Tree on Wikipedia

          Scape-Goat tree is a kind of binary search tree like Treap and Splay. But it makes itself balanced by reconstruction instead of rotation.Practically,if we find the size of the root's left son becomes larger than k*size of the tree or smaller than (1-k)*size of the tree,we just collect all its vertices and rebuild a new binary search tree.Usually k is set to be between 0.7 and 0.8.There is a proof why its complexity is O(nlogn) just as Treap and Splay.

          → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Could you please elaborate how would we solve this problem with segment tree and space-goat tree?

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Nice Substitute For Persistent Segment Tree.But how Can we add Update part to it?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +31 Vote: I do not like it

Published version Direct link to the paper :)

As one of the authors of the paper, if anyone has any doubt about the structure, my mail is [email protected]

Ps: A paper about how to answer the same querys in a Tree in an efficient and elegant way is going to be published soon ;)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What is the complexity of solving 3rd problem from the blog using wavelet tree? Also, can it support updates?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      You should read the paper :) the first question is answered in detail there. The answer for the simplest case when you have an array of N elements (in a reasonable alphabet, for example, numbers < 10^9) is O(lg(N)) per query.

      For the updates, in the paper we covered some cases, like toggling, adjacent-swapping, push_back and push_front.

      → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Hi, I'm trying to use wavelet tree for MKTHNUM problem on SPOJ, but I keep getting runtime error.

Can anyone tell me what's wrong with my submission? Code

I used the template and just changed the main function.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    i also copied those code too, but getting wrong answer instead. here is my submission ideone

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Have you used index compression? The numbers can be up to 10^9

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        thanks, i use index compression and got AC. I safely assume RTE in your submission is not related about the DS.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        does compression matter for getting the correct output?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Compression is needed due to the input constraint that can be up to 10^9. I don't think you can make any array of that size without compressing the value first..

          → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I also tried the same problem and im getting WA. I implemented by myself but I compared with some other codes and seems pretty much the same. Can anyone help me? code

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is it possible to support the following type of update using wavelet tree?

Given l, r, x, add x to all the elements from al to ar.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is It possible to delete Element Or Update the Value of element ?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, but you have to use something else instead of arrays to store the bitarray for efficiency

    I used a bst here

    → Reply
»
4 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

It would be great if you (rachitiitr)can write another blog explaining about Wavelet Trees.

→ Reply
»
4 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Link is broken :(

→ Reply
»
4 years ago, # |
← Rev. 3   Vote: I like it +9 Vote: I do not like it

I don't actually know the English name but there is indeed a similar data structure in China, called “主席树” or HJT seg-tree, and there are a bunch of problems like that in China.

The main idea was to save a single-point change of a segment tree in $$$O(\log n)$$$ memory & time complexity.

First, we do discretization for all numbers.

Second, we build an empty seg-tree with the size of n, we'll let it be version[0].

Then we let i from 1 to n, we make the element in place a[i] $$$+1$$$ and make a new version i (based on version[i-1])

Similar to prefix, all data of numbers in $$$a_l$$$ to $$$a_r$$$ will be in version[r]-version[l-1], we can than perform these operations in $$$O(\log n)$$$ time.

The total complexity will be $$$O(n\log n+q\log n)$$$

→ Reply
»
17 months ago, # |
  Vote: I like it 0 Vote: I do not like it

it's too bad this is named "wavelet tree". I feel "quick sort tree" is better, especially since it parallels "merge sort tree"

nme origin:

The name derives from an analogy with the wavelet transform for signals, which recursively decomposes a signal into low-frequency and high-frequency components.

https://en.m.wikipedia.org/wiki/Wavelet_Tree

→ Reply
»
4 weeks ago, # |
  Vote: I like it 0 Vote: I do not like it

I will take this blog to add my own comments about Wavelet Tree, since this is the only catalogue entry about wavelet tree.

Wavelet Tree at first glance seems useless. To solve the tasks as described, you can use merge-sort tree in $$$O(n log^2n)$$$, or $$$O(n log n)$$$ with fractional cascading (note that it cannot do k-th smallest without an extra log). The generally better option, is that you can use persistent segment tree, with a trick of multi-descend (see https://codeforces.net/blog/entry/79669 for an explanation), to also do this in $$$O(n log n)$$$. Indeed, when I initially tried out wavelet tree, both of these alternatives has basically the same speed as wavelet tree.

So all of the above are $$$O(n log n)$$$ memory with complexity $$$O(log n)$$$. n log n is the theoretical memory minimum, so what is the point?

The critical difference is that $$$O(n log n)$$$ memory does not discuss the constant factor. Wavelet tree only needs n log n bits! (not integers!), making it practically (n log n /32) memory. Wavelet tree is the only implementation that can take advantage of a bitset-like optimisation. This savings is very substantial on arrays with large size.

To actually take advantage of this, the most important vector b must really be a bit vector, and not just an integer array of prefix sum. You need to perform some bit operations to extract the prefix sum of the bit vectors, but as a profiler shows easily, the runtime is negligible compared to the time of memory access.

→ Reply