dheeraj_1997's blog

How to solve http://www.spoj.com/problems/SUMMUL/

By dheeraj_1997, history, 7 years ago, In English

Hi, I am struck at this problem http://www.spoj.com/problems/SUMMUL/ . I think this can be solved using Matrix Exponentiation but I am unable to come up with the recurrence relation for this. Can someone please guide me towards the equations for this problem.

  • Vote: I like it
  • +13
  • Vote: I do not like it

Comments Comments (14)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Let's also add a decomposition of n to the one term, the answer will be easier. Can you write any slow solution (DP or even bruteforce) to calculate it? It's really easy to guess the formula by values for small n.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Found the relation as you told: F(n) = 5*F(n-1)-8*F(n-2)+5*F(n-3)-F(n-4). But still can you tell me how to approach such type of problems? Thanks

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Your coefficients looks correct. But in my first sentence i meant that there is an easier way: let's consider a function g(n) = f(n) + n. 1, 3, 8, 21, 55. Something familiar, isn't it? I don't know how I came up with this, though.

      Generating functions are a rather universal way of solving such problems. I'm pretty sure that in this problem you can apply them, although I haven't tried.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 3   Vote: I like it +8 Vote: I do not like it

        We can write the recurrence relation as f(n + 1) = 3·f(n) - f(n - 1) + n and substituting g(n) gives g(n + 1) = 3·g(n) - g(n - 1) which is the bisection of Fibonacci sequence.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 10   Vote: I like it 0 Vote: I do not like it

          Once you get f(n+1) = 3*f(n) — f(n-1) + n you can solve it directly using matrix exponentiation. You don't need to reduce it again to a function g(n).

          F(n+1) = 3*F(n) + (-1)*F(n-1) + 0*F(n-2) + 1*n

          F(n) = 1*F(n) + 0*F(n-1) + 0*F(n-2) + 0*n

          F(n-1) = 0*F(n) + 1*F(n-1) + 0*F(n-2) + 0*n

          n = 0*F(n) + 0*F(n-1) + 0*F(n-2) + 1*n

          You can express the 4 eq's in the form of a matrix.

          Link:- http://zobayer.blogspot.in/2010/11/matrix-exponentiation.html.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            That's the standard thing to do after finding the recurrence, but it's much more satisfying to represent it in terms of a known sequence.

            → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

f(N) = fibonacci(2*N) — N. I used this formula

→ Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

We know that
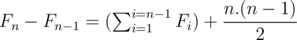Fn = 1(Fn - 1 + n - 1) + 2.(Fn - 2 + n - 2) + ...
Fn + 1 = (Fn + n) + 2.(Fn - 1 + n - 1) + ...
So, subtracting these terms we get
and .
Subtracting these terms again we get Fn + 1 = 3Fn - Fn - 1 + n. We are lucky in this case as we can substitute Fn = gn - n to remove the polynomial term and solve it using matrix exponentiation. However, in the general it might not be so. But nevertheless, we can still find the solution in such cases. For example, take a look at this article. recurrences

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is easy to see that F(n)=F(n-1)*1+F(n-2)*2+F(n-3)*3+... but where do the terms (n-1)+(n-2)*2+... come from? @I_love_Equinox

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You dont need to remove polynomial term, because if we store 1 and n in vector then n=(n-1)+1 and it is a linear transformation. Similarly n^2=(n-1)^2+2n-1 and so on.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      As I am a novice will you please explain a bit more clearly?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        Vector you need to maintain: v(n) = (F[n], F[n-1], n, 1). Just find a matrix A, so that A*v(n-1) = v(n). Then to find f(n) just compute (A^n)*v(0). If your polynomial terms were bigger your v would look something like: (f[n], f[n-1],1,n,n^2,n^3,...).

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks I didn't know that too,but my question was that how does one get to the basic recursive formula ?

          → Reply
»
5 years ago, # |
← Rev. 5   Vote: I like it 0 Vote: I do not like it

I went through the comments by others which were helpful, but how can I derive the basic recursive formula or is it just intuition?

→ Reply