Hello Codeforces Community!

I have been solving some interesting bitmasks problems. In some problems, we have to generate all possible subsets from a set. Obviously, if our set is a bitmask with all its bits on, we can iterate from 0 to 2ⁿ - 1

However, if we need to generate all the subsets from another subset (subset-ception), we can do it with the following procedure:

for(subset = set; subset > 0; subset = (subset - 1)&set)

(The code above ignores the empty subset)

Generate all the subsets from all possible subsets has O(3ⁿ) complexity. Now, I can intuitively confirm this, because we can represent our subsets as a string with 3 possible values: while 1 and 0 at position i means that the object i is in our subset or not respectively, 2 means that the object i is not present in the set at all.

However, mathematically:

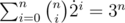
Amazing! I cannot find a way to prove this though. Do you know how to prove this interesting property?

Update: Solved, thanks! It was very simple :(