We are given an array of size N and Q queries (1 <= N, Q <= 100000). Each query has 4 parameters: index i, index j, length L, and differences D (0 <= D <= 1). We must answer "YES" if a permutation of the subarray from arr[i] to arr[i+L-1] differs from a permutation of the subarray from arr[j] to arr[j+L-1] in at most D places, and "NO" otherwise.
This sounds like an offline segment tree problem, but I am not sure how to start implementing it.
Can someone give me some hints to get me started and moving in the right direction?
Please help, and thanks in advance!
UPD: Just for the sake of it, I tried submitting a naive N^2 solution, which didn't make it in the time limit of 2 seconds, as expected.
UPD2: Original problem statement is here.











Auto comment: topic has been updated by vamaddur (previous revision, new revision, compare).
Can you give me link to problem statement? This statement is unclear
I didn't understand the permutation part clearly, but you can do the queries for any array (No need to be permutation) in O(D * lg(n)) by hash.
Can you further describe this approach?
First you will hash the whole array : hash[i] = hash[i - 1] * BASE + a[i] .
Now you can calculate the hash for each subarray in O(1) and two subarrays are different if and only if their hashes are different numbers.
Also you can find LCP (Longest Common Prefix) of two subarrays in O(lg(n)) by using binary search.
Now you can solve the problem by finding LCP, D + 1 times :
Tell if I made a mistake or completely misunderstood the problem :)
@Batman That solves the problem for D = 0, but I am kind of unclear on how to compute the hash in constant time.
That code I sent works for D>0 too.
The hash for subarray [l,r] would be this : hash[r] - hash[l - 1] * BASE(r - l + 1) .
Auto comment: topic has been updated by vamaddur (previous revision, new revision, compare).
How to compare two multisets A = {a1, ..., ak} and B = {b1, ..., bk}? Take a random function f. If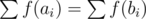 , most probably A and B are the same multisets. Otherwise they are different.
, most probably A and B are the same multisets. Otherwise they are different.
How to check if A and B differs only by one element? Suppose that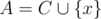 and
and 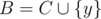 . We can get y - x by comparing sums. We can also get y2 - x2 by comparing square sums. Now we know x and y, and we can compare
. We can get y - x by comparing sums. We can also get y2 - x2 by comparing square sums. Now we know x and y, and we can compare 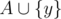 and
and 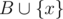 .
.
What kind of function are we talking about here? I assume a polynomial with at least degree 2 and prime coefficients?
In the first part, he is talking about functions in a general way. A constant function or any other that would not allow us to distinguish two numbers would not work, so we are looking for a bijection or a "almost" bijection.
On the second part of the answer he specifies two functions f(x) = x and f(x) = x*x. These functions let you find x and y. Of course you can use other functions if they allow you to solve the equations for x and y.
How can we prove what rng_58 has proposed ?
In general, you can't. He is using hash functions to compare sets. So there's always a probability that his method fails.
quite similar to this problem:https://www.codechef.com/JUNE17/problems/CLONEME
You can take a look of the AC codes. Hope it helps.
A O(n sqrt(n)) solution.
(No hash)
Step 1:divide the elements into sqrt(n) intervals.
Step 2:divide the queries into O(n) parts according to the intervals the leftmost&rightmost elements are in
Step 3:deal with the queries like this:
Now,we just need to ADD_ELEMENT/DEL_ELEMENT in O(1) time
Declare an array diff[MAX_ARR],which shows the difference of the times each numbers appears between arr[l,l+L) and arr[r,r+L) (possible negetive),and a variable DIFF which equals to the sum of all of the ABS(arr[k])),and it can also mean the minimum elements that 'a permutation of the subarray from arr[i] to arr[i+L-1] differs from a permutation of the subarray from arr[j] to arr[j+L-1]'
When adding/removing elements,we just change two of them,so the change of arr[] and DIFF can all be O(1) (I'm sorry I don't have a complete code)
Sorry for my poor English :)
UPD: I've found the English name of this algorithm: Mo's algorithm