Hello friends. The year is almost over so I have prepared the top 10 optimizations of 2017 for your viewing pleasure. Without forthor ado, let us begin.
OPTIMIZATION OF FLOYD VARŠAL ALGORITHM TO RUN IN N^2: simply instead of going from 1 to N in third loop we willuse bitset which will visit the remaining nodes automatically
SEGMENT TREE OPTIMIZATION TO RUN IN O(NlogMlogQ) complexity. We will simply use bitset to fetch our data between nodes instead of every time having to calculate hashes in nodes all over again.
OPTIMIZATION OF FENWICK TO ACCEPT QUERIES OF TYPE: EXPAND INTERVAL BY CONSTANT C We will simply use bitset which will store every expansion in every possible moment in time. You will say this is obviously too slow. But it can be easily optimized. We will simply make another bitset map for these changes.
USING LCA AS A TOOL TO OPTIMIZE TRIE You maybe thinking that LCA has nothing to do with trie. but-witg SIMPLE usage of little thing called bitset,. we can chsnge this. simply make bitset remeber on evrry turn where yoou ended up afta joining nodes into components. time complexity: o(QlogLoglogNM) it can be essily proven but i will leave it to readers prectis
COMPRESSING ENTIRE HASMHAP INTO A TRIPLET OF BINARY SEARCH TREES How? YOU WILLASK. i willsay: it csn be done with the help of our little mriemd bitset. we will simply store him into a SEPARATE container instead of keeping it with the other trees . This will also improve memory!!!! Readers practice
MULTIPLYING BIGNUMS IN O(LOG23.5NMQRSQRT(LOG(nm))) Simply store the factors inside a RB tree of bitsets and use improved FFT.
IMPROVED FFT Simply make bitset for every multiplication and merge them every logNth operation. You can not merge naively but it csn be easily merged via heuristic approach. readers prectis
CONCAVE HULL TRICK Ok. You ssy concave hull can not be used for quad tree optimization trick. It can. One word: bitset.
MACHINE LEARNING TRICK WITH BITSET Simply use AI bitset for storing your patterns.
REVOLUTIONARY OPTIMIZATION OF BLOCK CHAIN The circular implementation of a new hashing algorithm using to optimize proof of work concept. Hashing the last block with the nonce from the previous nth block as to make it circular.
thank you for your attention mriemds,
With respect. bukefala
Literature: https://arxiv.org/pdf/0909.4437.pdf http://www.amazon.com/Optimizing-energy-consumption-wireless-networks/dp/3659121207 http://www.superknjizara.hr/index.php?page=autor&idautor=13819 http://www.jucs.org/jucs_23_3/generating_politician_profiles_based http://authors.elsevier.com/a/1SQGc5aecSN1Bg https://arxiv.org/pdf/1705.07279.pdf











Tourist hates him! Such ANIMAL...
Number 5 shocked me, but how do I keep track of the hierarchy of the containers?
Simply use bitset.
Ahaaaaa i can't beliwve i missed that. Thanks this is awesome
Can you elaborate on number 1?
of course mriemd. ok so: if you do normal floyd varsal you will take k i j for loops and imrpove path from i to j though k. But it is n^3! So for final loop which chooses the j destination you can simply store the first part of the paths lengths in a bitset which will then automaticslly update the paths when you remove the loop j and cslculate with values previously stored in the bitset
wow such ANIMAL
Genius.
Why not use bitset in 10.?
I love the complexity of 6th.
I think you have a mistake in 6.
Real complexity is O(LOG23.5NMQRSQRT(SQRT(LOG(nm)))) (Because you can use a 2d bitset and get faster solution)
Ooooooh very nice idea to include 2d bitset. Thank you for sharing it!
Is this a joke?
No, these are serious optimisations. Look into this (http://www.cplusplus.com/reference/bitset/bitset/) and you will figure it out.
"The year is almost over"
Can you give a sample code for the first optimization? I still can't imagine how it work.
Are you serious? I personally don't think the first one's complexity is O(N^2). Could you please explain it more clearly?
I think he accidentally swapped the complexities of 1. and 6. because the "optimized" complexity of Floyd-Warshall really looks like O(LOG23.5NMQRSQRT(LOG(nm))).
If you use 3D bitset you can get
complexity :)
Yeah, excuse me for the typo.
Let alone the complexity,could someone please provide the sample code for the optimized Floyd-Warshall? I think maybe I misunderstand the process of the algorithm.
Here you go. Might be buggy, I didn't stresstest it.
Where's the main part of your programme? Why is there nothing in your loop ?
Because bitset takes care of it.
Why do I feel that I am being tricked by you guys? And now I begin to believe what mredigonda says.
ANIMALLL !!! Great optimizations!!
In fact, you can optimize bitset to use only O(1) memory. Just keep an additional bitset in each bit so that everything is stuffed into a single bit.
I can't believe there is a lot of people who actually thought this was true.
I only read #1, revised my memory of Floyd Warshall by going to Wikipedia, then spent 10 minutes trying to figure out how the optimization worked! XD This is a magnificent post! :D
Great optimizations
I need to bookmark this :P
9 is not very practical because you can't do gradient decent on Boolean values. And anyways, what do you get when you apply a bitset convolution on a bitset? It can't result in another bitset.
You can convolve two bitsets quickly in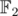 using Fast Walsh-Hadamard Transform, a variant of FFT. This algorithm actually has very short 3-line implementation using bitset library; I encourage you to find it.
using Fast Walsh-Hadamard Transform, a variant of FFT. This algorithm actually has very short 3-line implementation using bitset library; I encourage you to find it.
Does it get any better? Is there a reason for posting anything after this post came into existence?
Painting has Mona Lisa, sculpture has David, football has Maradona's goal against England, and Codeforces has this. Pure art.
This blog post is simply enlightening. It is the Bible of the bitset religion.
As I understand, bitset is just a compact representation. So, it should just improve the time by dividing by a constant (which is max 64 if we used a long instead of each bit) and this does not improve time complexity. So, how does it improve complexity?
We can optimize a bitset by using another bitset. This divides the constant every time by 64, and since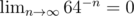 , the operation will eventually converge to O(1) if we use enough bitsets.
, the operation will eventually converge to O(1) if we use enough bitsets.
Basically, it belongs to a class of limit optimizations. Consider any algorithm A for a problem P, that brings down the complexity from f(P) to g(P) where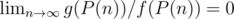 . Applying A sufficiently many times, you can bring down the complexity to g * which can be practically O(1).
. Applying A sufficiently many times, you can bring down the complexity to g * which can be practically O(1).
A trivial example of this is linear search to binary search. For P(n) = searching in sorted list of size n, f(P(n)) = n, but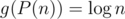 . The conditions for the optimization are satisfied, and consequently the complexity can be brought down to g * ≈ O(1).
. The conditions for the optimization are satisfied, and consequently the complexity can be brought down to g * ≈ O(1).
The idea is very trivial and frequently used by high rated coders, so I thought I should post it here for the benefit of the community.
Oh, I get it now. This was really easy. For 2018 post, you can add: Graph Isomorphism problem in polynomial time: Use 19 dimensional bitsets for node representation. Reference: https://people.cs.uchicago.edu/~laci/papers/icm18.pdf
Very nice explanation, my friend
bukefala: This is the best blog post in Codeforces.
I don't get it, how do you apply bitset optimization twice?
By using a bitset of bitsets, obviously
bitset<bitset<MAX_N>>doesn't work :( so, do we have to use templates?Also, won't the complexity be O(1 + log(n))? Because log(n) is the number of bitsets. I know it's almost O(1) but still.
You're too noob! It's very obvious just use bitset
It is easy. Just 2 lines of code per dimension. See https://www.geeksforgeeks.org/c-bitset-and-its-application/.
bitset <bitset > Works fine on my computer. Don't know what you're talking about.
Then bitset is Road to Grandmaster.
You forgot to mention that Traveler Salesman can also be solved in O(N) using bitset<bitset<bitset<bitset>>>.
?
Legend says that Fermat used n-dimensional bitset to prove his last theorem, but his margin was not enough to contain the code...
Can I see the code of OPTIMIZATION OF FLOYD VARŠAL ALGORITHM TO RUN IN N^2 ?
https://codeforces.net/blog/entry/53168?#comment-372098
Sorry but nothing is in there.
Looks like the NSA is hiding it. Don't ask any more.
Are you the inventor of the bitset?
So basically Bitset is a God?