Hi everyone!
tl;dr. If you write the following code:
void dfs_sz(int v = 0) {
sz[v] = 1;
for(auto &u: g[v]) {
dfs_sz(u);
sz[v] += sz[u];
if(sz[u] > sz[g[v][0]]) {
swap(u, g[v][0]);
}
}
}
void dfs_hld(int v = 0) {
in[v] = t++;
for(auto u: g[v]) {
nxt[u] = (u == g[v][0] ? nxt[v] : u);
dfs_hld(u);
}
out[v] = t;
}
Then you will have such array that subtree of  correspond to segment
correspond to segment 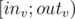 and the path from
and the path from  to the last vertex in ascending heavy path from
to the last vertex in ascending heavy path from  (which is
(which is 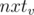 ) will be
) will be 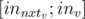 subsegment which gives you the opportunity to process queries on pathes and subtrees simultaneously in the same segment tree.
subsegment which gives you the opportunity to process queries on pathes and subtrees simultaneously in the same segment tree.

Inspired by Vladyslav's article and Alex_2oo8's problem Persistent Oak. You can find my solution to this problem here to learn how it can be used to maintain persistent hld over the tree.











Hi, big fan of your blogs!
Could you elaborate a bit on how modifications work? The fact that each node has two positions (in, out) and not both are contained in the path query confuses me on how to handle updates and queries both simultaneously. I'd think we need to make sure modifications change both in(v) and out(v) when modifying v for any reason.
Hi.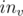 and
and 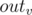 will not change, they just indicate borders of subarray corresponding to subtree of
will not change, they just indicate borders of subarray corresponding to subtree of  .
.
Yes, I mean the values for the nodes in_v and out_v in the segment tree.
Oh, you got it incorrectly. Each node occur only in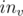 position.
position.
Ah, the out is only a marker. No wonder t doesn't increase when setting out, that was bugging me. All clear now, thank you.
Is this a specific version of HLD or a short version?
This is short version which also allows you to easily make queries to subtrees.
Does it become the normal hld without queries when we comment the lines that contain in and out? Haven't learnt this data structure yet so I try to have a sense about its implementation. This is the neatest implementation I've ever seen and it made me motivated learning about it.
What do you call normal hld? It's hld only if you don't use out array.
Very cool and concise implementation, thank you!
This blog is 6 months old, but I've just read it and... WOW WOW WOW WOW, it's so great, WOW WOW (sorry, I just have to do it) WOW WOW WOW!!!
Somehow I also missed this post, and I confirm that this trick is ultimately cool.
Well, I'm kind of surprised that you guys didn't know that trick. There was a problem about 2 years ago (which is a way simpler than a problem mentioned in this post).
PS: I understand that top coders do not care much about HR, codechef, etc. So it's probably ok.
They are not surprised by technique called HLD which is well known. They are surprised by the fact how easy can it be made in terms of implementation.
Yeah, it makes sense :)
Not only, but also the fact that batch updates may be performed over subtrees and arbitrary paths across the tree simultaneously using the single segment tree built across the traversal of the tree.
For example, now I know how to solve the following problem: given a tree on n vertices and q queries of form 1) add x to all numbers in the subtree 2) add x to all numbers on the path 3) find maximum number in the subtree 4) find maximum number on the path, answer all queries in O((n + q)log2n)
OMG, I feel so stupid for not realizing that this in fact enhances functionality, I thought that this one common segtree is just for convenience and swag. Thanks for pointing this out.
Cool. I wish had known this approach offering this task: https://www.hackerrank.com/challenges/subtrees-and-paths
I am confused here. Can someone please explain me how this works?
Does it require two segment tree or just one to solve problem mentioned by Svyat using above method ? How will you do lazy update to add values in subtree rooted at u? and query for maximum in path?
Is it ok that the code doesn't use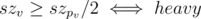 property?
property?
Sure, I just say that heavy edge is which lead to the largest subtree. Obviously it's better for implementation and time complexity is not worse.
Maybe we don't really need the array out[], since out[u]=in[u]+sz[u]?