Two contests AtCoder Regular Contest 078 and AtCoder Beginner Contest 067 will be held at the same time.
You can participate in whichever contest you want. (However, you can't register to both competitions.) The last two tasks in ABC are the same as the first two tasks in ARC.
Time: July 15th (Saturday), 21:00 JST
Duration: 100 minutes
Number of Tasks: 4
writer: camypaper
Rating: 0-2799 for ARC, 0-1199 for ABC
The point values will be announced later.
We are looking forward to your participation!
UPD:
The point values are announced.
It is 100 — 200 — 300 — 400 — 800 — 900.











The point values are announced. (Link)
It is 100 — 200 — 300 — 400 — 800 — 900.
UPD: Thank you for updating blog.
I decided first time to participe on AtCoder contests and registered for Regular round. Than I decided that I want to do Beginner contest ( I think I am not ready for such big jump in competetive programming ), so I wanted to unregister and register again to different round, but there is not such option ( or I can not see it )...
If anyone know way, it would be nice to help me :)
If I try little hard I can solve all problems in beginner contest, Your rating is high from mine. So it's easy to you.
I think you should participate in regular round, because beginner rounds are easier than div2.
@Emilbek, Len
I believe you are right about participation. But after exam at university, unrated CS Academy contest and two bad CF rounds for me, I wanted to feel as genious who can solve everything at some round :D Normally it is possible to fail again, but than I would fail on regular contest too.
In addition, AtCoder Beginner Contest's maximum performance is 1600, even if you get 1st place. But AtCoder Regular Contest's maximum performance is 3200, so I think you should participate in regular round. (Rating approaches performance asymptotically)

allllekssssa You are purple. Have confidence!!!
Sorry for my poor English.
How did you solve Fennec VS. Snuke?
Look at the path from 1 to n. First they will color whole path ( half one color half other). Than erase path you will get forest ( several trees ) . In each tree you will have one color and that whole tree will be colored on that way. So just count amount of nodes in "black root" trees and "white root" trees and see what is bigger.
I really hate interactive problems, I came up with solution very fast, but I didn't get AC :(
Is the last task some bitmask + max flow min cost algorithm ?
I also did this but I couldn't get accepted. Can anybody help me please? Code
Root the tree at vertex 1, now in optimal game snuke goes up some vertices up and paints the whole subtree white. So, just check the vertices the snuke can go and take the maximum subtree.
I used a BFS maintaining 2 queues (black and white) and a distance array maintaining layers from nodes 1 and n. if a node from black has color black (let's call it t1), the distance of all it's adjacent nodes is d(t1)+1. if d(t1)+1 <= d(adjacent node) i will color it black and add it to queue. Similar thing can be done with white queue but one difference: add to white only if d(t2)+1 < d(adjacent node).
I solved by this algorithm.
1. Calculate dist(1, 1), dist(1, 2), ..., dist(1, N) and dist(N, 1), dist(N, 2), ..., dist(N, N).
2. Define two integer a, b. Initially these two are 0.
3. For each i: if dist(1, i) ≥ dist(N, i) a++, otherwise b++.
4. a means the number of vertex which can get Fennec, and b means the number of vertex which can get Snuke.
5. So if a > b, Fennec wins. Otherwise, Snuke wins.
This algorithm is correct because there is no more than one vertex which is dist(1, i) = dist(N, i).
My code is here. Sorry for my poor English.
Aha, I sovle by this meassure too
What I did was
First maintain two array level1 and level2
Bfs from 1 and store all the values of level of all the nodes in level1
Bfs from N and store all the values of level of all the nodes in level2
Then
Consider some vertex is painted in black at any stage of the game. Consider many components you will get when you remove current black vertex. One of that components will initially contain white vertices. White will never paint a vertex in any other component during the rest of the game. So black will paint them when the time comes in any case.
So an optimal strategy for both players will be to paint next vertex on the shortest path from vertices 1 to n. In that way, they will potentially increase the number of vertices to paint in future for themselves.
When the path is painted, you can simulate the process to see who will win. Or you can say that 1 is a root, calculate the size of the subtree for every vertex, compare the number of vertices in the subtree of the highest vertex the black player can get to with the remaining number of vertices in the whole tree.
There is no need to find path from 1 to N or to compute any distances; one queue for bfs is enough. First vertex in queue is 1, it's colored black; second vertex is N, it's colored white; problem is solved with usual bfs — in one step just color all adjusting uncolored vertices the same color current vertex has, and add those to queue. And then compare sizes of two components (if black > white Fennec wins, otherwise wins Snuke).
Any Hint for Awkward Response?
? 1
? 10
? 100
? 1000
? 10000
...
2. Use binary search to get number. Since to be always n > N, the question number n should be multiple by 10. (This means if the number of digits of N is 2, the number of digit of n should be 3.
If the number is 42:
First, L = 100, R = 1000 because 42 is a 2-digit number.
Obviously, n > 42 if N is 100 or more. So if str(n) > str(42) the answer will be Yes.
So if n ≥ 420 the answer will be Yes. You can search this by binary search.
The code is here. Sorry for my poor English.
How did you solve Mole and Abandoned Mine?
Um_nik uwi vintage_Vlad_Makeev ACRush izban
Please decribe your solution.
The editorial is uploaded!
Why don't you mention arsijo yosupo kmjp sugim48 VArtem latte0119 sigma425 fetetriste TimonKnigge khadaev ei133333 chenmark maroonrk Hasan0540 btk15049 ? They also solved problem F in the contest.
I picked only top 5.
Hope this intuitive thing helps (see the editorial for details and formal proof). Let S be the set of vertices that are already "determined", and u be the last vertex on the "determined" path. Do bitmask DP over S and u (f[S][u] is the maximum sum of edge weights under that state, every time we take another u and another set to add into S), and try to prove it works in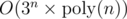 rather than 4n stuff.
rather than 4n stuff.
For Problem E Awkward Response, is it possible to know the value of N for test cases 2,5,7,14,30?