Two contests AtCoder Regular Contest 079 and AtCoder Beginner Contest 068 will be held at the same time.
You can participate in whichever contest you want. (However, you can't register to both competitions.) The last two tasks in ABC are the same as the first two tasks in ARC.
Time: July 29th (Saturday), 21:00 JST
Duration: 100 minutes
Number of Tasks: 4
writer: yosupo
Rating: 0-2799 for ARC, 0-1199 for ABC
The point values are
ARC: 300 — 600 — 600 — 800
ABC: 100 — 200 — 300 — 600
We are looking forward to your participation!
Let's discuss after the contest.











I have no idea why my submissions works that fast(3ms on official tests), can anyone tell me its complexity? http://arc079.contest.atcoder.jp/submissions/1467261
In every iteration of the outer loop, the largest number A decreases to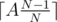 in the worst case. The ceil doesn't really matter, it is still
in the worst case. The ceil doesn't really matter, it is still 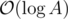 steps to reduce it to N - 1.
steps to reduce it to N - 1.
In problem F , what was the point of mentioning weakly connected graph. I think almost similar algorith works even if it is not weakly connected.
If a graph was not weakly connected you can have more than (m + 1) edges in a subgraph having m vertices, so it's harder.
Edit: Forgot about the way edges were given, the above is incorrect.
How is that possible? I think that with edges pi->i you can have at most m edges in a subgraph with m vertices and that doesn't depend on connectivity.
Yep, you're right, I forgot that the edges were given in such a format, of course you cannot have more than one edge going into any vertex.
You can have something like:
6
3 1 2 6 4 5
Which means that there can be more than one cycle. You will just have to run that algo for each odd cycle but I can't think of any corner cases related to this.
That assumption made the problem more convenient — you could focus on the main idea.
How to solve Problem D and E??
First, we forget about the fact that we choose the maximum value. As long as at the end 0 ≤ ai < n, the sequence of operations can be transformed into a valid one. (Sketch of proof: look at the first position where we took a non-maximum. In the remaining part there must be an index that is current maximum, otherwise we would end up with a too big value. We swap the values.)
Now, we are only interested in counts of operations done for each index. Let these be mi. We have 0 ≤ ai - mi·(n + 1) + k < n and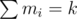 .
.
For problem D, I chose n = 50, mi = k / n or mi = k / n + 1 so that they sum to k. Then I chose ai such that the value in inequality is n - 1. My code.
For problem E, we can sum the inequalities over all i and get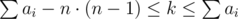 which gives us at most n·(n - 1) values of k to check. For a fixed k, we can solve the inequality for mi and see if the solution exists and sums up to k. My code.
which gives us at most n·(n - 1) values of k to check. For a fixed k, we can solve the inequality for mi and see if the solution exists and sums up to k. My code.
There is also a different solution in editorial (scroll down for English version).
Sorry But I am not getting inequality obtained in E that you mentioned.Can you please tell to obtain it ???
We have inequality 0 ≤ ai - mi·(n + 1) + k ≤ n - 1 (changed the right part to ≤ ). We sum it over i and get
But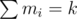 so it is the same as
so it is the same as 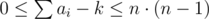 . By rearranging both inequality parts separately, we get the bounds on k.
. By rearranging both inequality parts separately, we get the bounds on k.
Thanks !!!
can u pls explain how u derived first eq.?? i don't get when and what values to swap. can u explain it a bit more naively.
The swap is irrelevant in the derivation of the inequality. It was one of many ways to prove the claim that we don't care about order of the operations. I'll assume the claim and focus on the equation but if you want to see details of the proof then ask.
If the order is irrelevant, we are only interested in how many times each index is chosen. Let's call it mi. We know that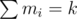 because these are all operations we make.
because these are all operations we make.
Each operation done on index i subtracts n from the value ai. There are mi such operations. Each operation done on index different than i adds 1 to ai. There are k - mi such operations.
The final value after all operations is ai - n * mi + (k - mi) = ai - (n + 1) * mi + k. On the other hand, a correct final array contains values between 0 and n - 1 inclusive, so we come to the final inequality 0 ≤ ai - (n + 1) * mi + k ≤ n - 1 that has to hold for each i.
it's all clear now, probably i didn't got what mi represents which was the main part may be bcz my english is poor or i read in hurry.
thanks for explanation!!
how to search the standings by user name?
In standings page, press CTRL + U (or view source) and search there...
thank you
For problem F, the editorial says the solution in O(N). However all the solutions I have seen use some form of sorting and/or loop to calculate mex number. What's the complexity to calculate mex number? Should this be included while determining the complexity of the solution?
You're right that the analysis is a bit brief. The simplest approach to find the label of v is to store the labels of all vertices adjacent to v, sort them and do one linear search. The length of this list is equal to the out-degree of the vertex. Since there are exactly N edges, the sum of all out-degrees is also N, and hence calculating all the mexes needs .
.
I can think of three ways of making this linear:
Stripping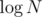 factor was of course not needed.
factor was of course not needed.
Could you please explain hash-function approach?
Sure. You maintain hash table for every vertex. Initially all hash tables are empty. To find a mex for vertex v, you find the smallest non-negative number absent in Hv. Denote this by Mv. You can clearly find this number in Mv + 1 hash table lookups. Vertex v has a unique predecessor u (there is exactly one edge (u, v)), you add Mv to Hu.
The rest of the analysis is similar to the latter approaches: there are n inserts to hash tables, and at most 2n queries.
A little simpler solution to F: