Hello Everyone-I am not able to get the solution of this problem ( http://codeforces.net/problemset/problem/835/C ). If any one can explain the solution of this problem.Thanks in advance.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 150 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.12.2024 19:44:34 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











The problem statement says that there are stars located in the sky. A particular star is located at position x,y and its starting brightness is s. The maximum brightness of every star is c.
The brightness for a particular star varies like this:-
Now in problem you are given queries: In each query we have t x1 y1 x2 and y2 In each query you need to find the total brightness of all the stars which are located in the rectangle with lower left corned x1 y1 and upper right corner as x2 y2 at an instant t.
Thanks buddy for your reply but can you please explain solution ? I am looking for that only.I am unable to understand
coz the brightness for a particular star is s[i] + t mod c + 1 where t refers to the time
Thanks a lot.
Hi Amit! First of all, pretty much every Codeforces round has a tutorial after-the-fact; for Round #427, it's right here: http://codeforces.net/blog/entry/53588. They can often be hard to understand, but I think there's worth in stretching yourself and trying to piece together the solution yourself from a few hints you can glean from the editorials.
That said, to actually answer the question:
Let's ignore both the brightness of the stars and the increase in their brightness for now. What if all we wanted to do was know, for a given x1, y1, x2, and y2, how many stars there were within that rectangle? Well, assume we had a 2D matrix stars[101][101] (0-indexed), where for all i, j, stars[i][j] = the # of stars in the rectangle (1, 1) to (i, j). If we had such a matrix, we could calculate the # of stars within the rectangle (x1, y1) to (x2, y2) as:
stars[x2][y2] + - stars[x1 - 1][y2] + - stars[x2][y1 - 1] + stars[x1 - 1][y1 - 1]
See the below pictures (shamelessly stolen from GeeksForGeeks) for why this works. We get Sum OB from stars[x2][y2], then subtract out the sides, but that takes out Sum OC twice, so we add it back in once. This is also an instance of the inclusion-exclusion principle.
So how do we construct this matrix? Let's first start from another matrix, pos[101][101], where pos[i][j] = the number of stars that are exactly at (i, j). Then, stars[i][j] = stars[i - 1][j] + stars[i][j - 1] - stars[i - 1][j - 1] + pos[i][j], for the same reason as the pictures above. So we can just construct stars[][] by looping over all i and j, starting from 0. The way to create pos[][] should be obvious.
That's all well and good, but now we actually have to consider the brightness. Let's continue ignoring the increasing brightness for now. We were only asking for the total number of stars in a rectangle up to now, but let's change that to asking for the number of stars within a rectangle of a certain starting brightness. However, if we look at the problem statement, we notice that the max brightness, c, is at most 10 — super small! So instead of maintaining a single stars[][] matrix, we could maintain (at most) 11; stars[b][i][j] will now be the # of stars in the (1, 1) to (i, j) rectangle, with exactly starting brightness b.
And finally, the increasing brightness. The thing to notice here is that all stars increase in brightness at the same rate. So if you know the time is t, and you've found some # of stars of a certain starting brightness b, you also know that all of those stars will have the same brightness at time t! Since the brightness keeps increasing by 1 at each time tick, and rolls over once it hits the max brightness c, any star that starts at b will have brightness (b + t) % (c + 1), at time t.
So, if you have the number of stars of a certain starting brightness within a certain rectangle, and the time at which you're looking at them, you use that formula to figure out what the brightness of each of them is and multiply it by the number of stars to figure out their total brightness. Repeat that for each possible starting brightness, and you've the answer to each query. Querying the stars[][][] matrix for each brightness is constant time, so you can answer each query in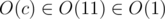 time.
time.
Thanks a lot.It really helped me.