Hi!
Hints
A: Let Cost(k) the answer if we compress the image with k, find min Cost(k).
B: Solve the problem without first query.
C: Let the frequencies of the characters be a1, a2, ..., ak. Alice loses if and only if 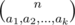 is odd and n is even.
is odd and n is even.
D: Consider adding an extra seat, and the plane is now circular.
E: Let dpi, j be the longest path given that we've included segment i, j in our solution, and we are only considering points to the right of ray i, j (so dpi, j and dpj, i may be different).
F: We want to compute dpi, j: expected value given we have seen i red balls and j black balls.
Solutions
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
P.S. Please notify me if there are any problems.











In A I didn't get idea of calculating number of ones in O(1) (and feel kinda stupid) so I submitted O(nmπ(max(n, m))) solution hoping to get partial score and got AC in 1.8s (idea is that there's no sense to make k composite)
The idea of finding the amount of ones in O(1) in a given rectangle is the same as finding the sum of segments in a normal array in O(1) (using prefix sums). we're going to make a table T, so that at indicies i, j (T[i][j]) you will see the amount of ones in the rectangle with top left corner at (0, 0) and bottom right corner at (i, j).
Suppose you need to find the amount of ones in the rectangle whose top left corner is (r1, c1) and bottom right corner at (r2, c2). Then the answer is T[r2][c2] + T[r1 — 1][c1 — 1] — T[r2][c1 — 1] — T[r1 — 1][c2]. (This is obviously O(1)) You may draw it on a piece of paper to make it more clear.
Yeah thanks I know that, just didn't thought about that when it was necessary. I mean I didn't get an idea during the contest. Sorry for inexact formulation:)
Oh well, suppose you decide the size K of the rectangles which you need to "fix". Note that by choosing K you also know the locations of the squares which you need to fix. Now, in order to fix a square, you need to either turn all the 1's in it to 0's, or turn all the 0's to 1's. Note that if the amount of 1's in a given square of K*K is X, then the amount of 0's is K*K — X. So the minimal cost to fix the square is min(X, K * K — X).
Using this, you can brute force every possible K from 2 to 2500, and it would still be fast enough (for each size K you pick there are N * N / K squares for which you need to check the cost to fix them, so the total time it would take you in worst case is 2500*2500 / 2 + 2500*2500 / 3 + 2500*2500 / 4 + .... , which ends up to be fine).
Edit: My bad I did the complexity calculation wrong :P. it is actually 2500*2500 / (2*2) + 2500*2500 / (3*3) + ... + 2500*2500 / (2500*2500), which is much less...
Can you explain in details? I didn't get the idea...
The first thing you want to do after the input is to make another 2D table, with the same size as the input table, and build it using dynamic programming (I'll explain in a second).
From now we'll define a rectangle as: (r1,c1)(r2,c2), which means a rectangle with upper-left corner at row "r1" and column "c1" (a rectangle in a 2D array), and with bottom-right corner at row "r2" and column "c2".
Now, the idea in the table built using DP (we'll call the table DP) is that at the cell in row "i", and column "j", we'll have a value indicating the amount of 1's that appear in the input at the rectangle (0,0)(i,j).
The way of building the table is as follows: (The input table will be named T and the dp table will be named DP): DP[0][0] = T[0][0].
DP[0][i] = DP[0][i — 1] + T[0][i].
DP[i][0] = DP[i — 1][0] + T[i][0].
The above are the basic cases, from there: DP[i][j] = DP[i — 1][j] + DP[i][j — 1] — DP[i — 1][j — 1] + T[i][j]
Explanation of the dp: - the case of DP[0][0] is pretty obvious; 1 if the cell T[0][0] is 1, 0 otherwise.
Both cases of DP[0][i] and DP[i][0] are the same: notice how it is identical to building a Prefix Sum array.
The last case which builds the whole table: We need to find the amount of 1's at rectangle (0,0)(i,j). We take the amount of 1's in rectangle (0,0)(i-1,j) (one row less) and add the amount of 1's in rectangle (0,0)(i,j-1) (one column less), but notice that we counted twice the rectangle (0,0)(i-1,j-1) (it's being summed in both the previous rectangles), so we decrease its value, and lastly we add the single value, T[i][j], to check whether there is a 1 in the bottom-right corner.
Now how do we find the amount of 1's in a given rectangle (a,b)(c,d)? We first take DP[c][d], so now we have rectangle (0,0)(c,d), then we decrease DP[a — 1][d], so now we have rectangle (a,0)(c,d), then we decrease DP[c][b — 1], so now we have just rectangle (a,b)(c,d), HOWEVER notice that we subtracted twice the rectangle (0,0)(a-1,b-1), so we must add back DP[a — 1][b — 1]. Therefor we come up with:
Amount of 1's in rectangle (a,b)(c,d) = DP[c][d] — DP[a — 1][d] — DP[c][b — 1] + DP[a — 1][b — 1].
Now, let's recall what we're asked in the task. We need to find such K, so that in all squares of size K*K, we'll need to turn them either completely to 1's, or completely to 0's, and then we need to find the K for which the amount of total operations on all squares is minimal.
Important note: suppose we picked some random K. The squares must be: (0,0)(K-1,K-1) (0,K)(K-1,2*K-1) (0,2*K)(K-1,3*K-1) ....
(K,0)(2*K-1,K-1) (K,K)(2*K-1,2*K-1) (K,2*K)(2*K-1,3*K-1) ....
. . . And so on. For each of these squares we can find in O(1) the amount of 1's they contain, using the rule we found earlier. Suppose we look at a K*K square, and we found it has X amount of 1's inside of it. If we want to turn this square into completely 0's, we need to change every 1 to 0, so the amount of operations is X. If we want to turn this square into completely 1's, we need to change every 0 to 1. Note that a square can contain only 0's and 1's, so if we know its size and we know exactly how many 1's it contains, we also know how many 0's it contains: K * K — X. This is amount of operations we need to do to turn the square into completely 1's. Now, we need to minimize the amount of operations. That means we need to pick the minimal value of the above 2: min(X, K * K — X). We find this value for each square of size K * K, add up all the values, and this is the minimal amount of operations we need to do if we take squares of size K * K.
Now all you need to do is go over all possible K sizes (from 2 to 2500), and maintain the minimal result you found.
That is the answer to the problem, I hope I was crystal clear this time because I don't think I can do any better.
Can you explain what is "dynamic programming"? I had never heard about this algorithm before.
Hilarious, I'm on the fence from exploding out of laughter. Guess I shouldn't be helping anymore to people when I think they need help.
So are the people you are explaining to, I believe :D
Yeah I already got the pathetic joke. At first I thought the first person needed help, then I thought I was unclear. Whatever I'm leaving this bullshit.
It was funny but I'm very sad at the same time because of looong explanation :(
Solution of D is really cool, I like it
Can you elaborate the solution a bit ?
I think this is what the formula represents:
(2*(n+1))^m — The ways of assignment without restrictions
1/(n+1) — Note that as the seats are in a ring, each of them have an equal chance of being empty
(n+1-m) — As there are (n+1-m) seats remain empty at the end, and again, they have the equal chance of being empty, so the ways of assignment that leaves a particular seat empty is multiplied by (n+1-m).
Thanks
About D's solution, is this some common trick when approaching similar combinatorial problems? If yes, can somebody please give some more problems in which it's applicable since it sounds really cool and simple once you know it but I'm pretty sure there was no way for me to come up with this.
I have came across this trick only once before, try this: https://www.hackerrank.com/challenges/number-of-subsets/problem
Consider bijections between sets with different xor value
Edit: This is for deriving the formula, if you are looking for the "make it circular" trick this is not the case. :(
Thanks for trying to help but what I meant was the trick with adding an additional seat to make the whole thing circular and then everything becomes easy. I guess I wasn't clear enough, sorry for that.
Can someone explain why odd n is a winning position in problem C?
We will proof by induction with the base case n = 1, and the current player could win by removing the only character.
Now we propose that when n is odd, it's a winning position as long as the string haven't been permutated yet, under this assumption, it follows the first sentence of the editorial (as the first who exhausts all permutations is forced to remove a character and forfeit the winning position to the opponent). Refer it as "losing even n situation" below.
For n > 1:
Case 1: n is odd && unique_permutations%2 == 1
Note that unique_permutations == C(n, a1,a2,...,ak) as mentioned in the editorial. If we remove an i-th alphabet from the string, it becomes C(n-1, a1,a2,...(ai-1),...ak) = C(n, a1,..,ak)*ai/n. As n is odd, there is at least one odd number in the set {a}, thus there is always a valid move to transform the string into a "losing even n situation".
Case 2: n is odd && unique_permutations%2 == 0
If there is no way to get to a "losing even n situation", then you can fatigue your opponent and force him to do the work for you, else you will just take the chance and force your opponent into the corner (You could actually prove that the latter case is impossible, you can prove it by yourself if you wish =] ).
Therefore case 1 and case 2 are both winning position, i.e. when n is odd, the first player always win, derived from the base case n = 1.
How do you convolute the dp states in problem C? I tried to use FFT but even long double can't handle the precision error as the values can be as large as 1e16? Should I scrap the idea of using fourier transform, or is it possible to applay modulo operations when going through FFT?
The problem is solvable without FFT. Take a look at codes.
Nice editorial.But why are you guys downvoting him?
In problem B , when u is not an ancestor of v,then I can go to any descendant of u( any element in subtree of u) ,then go to the root ,and then go to v . I didn't get the part where you said we have to go to a leaf from u ,why is it necessary that before going to the root we HAVE to go to a leaf ,why can't we go to any descendant of u and then to the root and then to v.Why is going to a leaf before going to the root guaranteed to give the minimum answer?
You are right. Sorry and thanks. Fixed.