Hi, dear contestants!
With the end of Codeforces Round #431 (Div. 1 and Div. 2), some might be complaining behind the screen that problems are too tricky or hard, or have been struggling with some supposedly solvable problem... Yes, this time problems seem hard, but anyways, I hope they provided you with something, say rating, fun, ideas, or experience. I don't want to see anyone losing confidence because of failure (bad luck) in a single contest — please, don't do so.
Here are the hints, tutorials and codes for the problems. Feel free to discuss about problems in the comments, and point out if something is incorrect or unclear. Thank you!
849A - Odds and Ends
by cyand1317
What will the whole array satisfy? Is that a sufficient condition?
#include <cstdio>
static const int MAXN = 102;
int n;
int a[MAXN];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &a[i]);
puts((n % 2 == 1) && (a[0] % 2 == 1) && (a[n - 1] % 2 == 1) ? "Yes" : "No");
return 0;
}
849B - Tell Your World
by cyand1317
First way: consider the first three points. What cases are there?
Second way: consider the first point. Either it's on a single line alone, or the line that passes through it passes through another point. Iterate over this point.
#include <bits/stdc++.h>
#define eps 1e-7
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,a[1007];
bool vis[1007];
bool check(double k,int b)
{
memset(vis,false,sizeof(vis));
int cnt=0;
for (int i=1;i<=n;i++)
{
if (a[i]-b==1LL*k*(i-1))
{
vis[i]=true;
++cnt;
}
}
if (cnt==n) return false;
if (cnt==n-1) return true;
int pos1=0;
for (int i=1;i<=n;i++)
if (!vis[i]&&pos1==0) pos1=i;
for (int i=pos1+1;i<=n;i++)
if (!vis[i])
{
if (fabs((double)(a[i]-a[pos1])/(i-pos1)-k)>eps) return false;
}
return true;
}
int main()
{
n=read();
for (int i=1;i<=n;i++)
a[i]=read();
bool ans=false;
ans|=check(1.0*(a[2]-a[1]),a[1]);
ans|=check(0.5*(a[3]-a[1]),a[1]);
ans|=check(1.0*(a[3]-a[2]),a[2]*2-a[3]);
if (ans) printf("Yes\n"); else printf("No\n");
return 0;
}
#include <cstdio>
#include <algorithm>
static const int MAXN = 1004;
int n;
int y[MAXN];
bool on_first[MAXN];
bool check()
{
for (int i = 1; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if ((long long)i * (y[j] - y[0]) == (long long)j * (y[i] - y[0]))
on_first[j] = true;
else on_first[j] = false;
}
int start_idx = -1;
bool valid = true;
for (int j = 0; j < n; ++j) if (!on_first[j]) {
if (start_idx == -1) {
start_idx = j;
} else if ((long long)i * (y[j] - y[start_idx]) != (long long)(j - start_idx) * (y[i] - y[0])) {
valid = false; break;
}
}
if (valid && start_idx != -1) return true;
}
return false;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &y[i]);
bool ans = false;
ans |= check();
std::reverse(y, y + n);
ans |= check();
puts(ans ? "Yes" : "No");
return 0;
}
848A - From Y to Y
by cyand1317
For a given string, how to calculate the cost?
For each letter, count how many times it appears in the original string.
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using D = double;
using uint = unsigned int;
template<typename T>
using pair2 = pair<T, T>;
#ifdef WIN32
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
int main()
{
int k;
scanf("%d", &k);
for (int i = 0; i < 26; i++)
{
int cnt = 1;
while ((cnt + 1) * cnt / 2 <= k) cnt++;
k -= cnt * (cnt - 1) / 2;
for (int j = 0; j < cnt; j++) printf("%c", 'a' + i);
}
return 0;
}
#include <cstdio>
#include <vector>
static const int MAXK = 100002;
static const int INF = 0x3fffffff;
int f[MAXK];
int pred[MAXK];
int main()
{
f[0] = 0;
for (int i = 1; i < MAXK; ++i) f[i] = INF;
for (int i = 0; i < MAXK; ++i) pred[i] = -1;
for (int i = 0; i < MAXK; ++i) if (f[i] != INF) {
for (int j = 2; i + j * (j - 1) / 2 < MAXK; ++j)
if (f[i + j * (j - 1) / 2] > f[i] + 1) {
f[i + j * (j - 1) / 2] = f[i] + 1;
pred[i + j * (j - 1) / 2] = j;
}
} else printf("Assertion failed at %d\n", i);
int k;
scanf("%d", &k);
if (k == 0) { puts("a"); return 0; }
std::vector<int> v;
for (; k > 0; k -= pred[k] * (pred[k] - 1) / 2) {
v.push_back(pred[k]);
}
for (int i = 0; i < v.size(); ++i) {
for (int j = 0; j < v[i]; ++j) putchar('a' + i);
}
putchar('\n');
return 0;
}
848B - Rooter's Song
by cyand1317
When do dancers collide? What changes and what keeps the same?
Group dancers by p - t. What happens next?
#include <cstdio>
#include <algorithm>
#include <vector>
static const int MAXN = 100004;
static const int MAXW = 100003;
static const int MAXT = 100002;
int n, w, h;
int g[MAXN], p[MAXN], t[MAXN];
std::vector<int> s[MAXW + MAXT];
int ans_x[MAXN], ans_y[MAXN];
int main()
{
scanf("%d%d%d", &n, &w, &h);
for (int i = 0; i < n; ++i) {
scanf("%d%d%d", &g[i], &p[i], &t[i]);
s[p[i] - t[i] + MAXT].push_back(i);
}
std::vector<int> xs, ys;
for (int i = 0; i < MAXW + MAXT; ++i) if (!s[i].empty()) {
for (int u : s[i]) {
if (g[u] == 1) xs.push_back(p[u]);
else ys.push_back(p[u]);
}
std::sort(xs.begin(), xs.end());
std::sort(ys.begin(), ys.end());
std::sort(s[i].begin(), s[i].end(), [] (int u, int v) {
if (g[u] != g[v]) return (g[u] == 2);
else return (g[u] == 2 ? p[u] > p[v] : p[u] < p[v]);
});
for (int j = 0; j < xs.size(); ++j) {
ans_x[s[i][j]] = xs[j];
ans_y[s[i][j]] = h;
}
for (int j = 0; j < ys.size(); ++j) {
ans_x[s[i][j + xs.size()]] = w;
ans_y[s[i][j + xs.size()]] = ys[ys.size() - j - 1];
}
xs.clear();
ys.clear();
}
for (int i = 0; i < n; ++i) printf("%d %d\n", ans_x[i], ans_y[i]);
return 0;
}
848C - Goodbye Souvenir
by adedalic
Difference between last occurrence and first occurrence equals the sum of differences between pairs of adjacent occurrences. Handle this with some segment tree, or even non-standard size block decomposition, say sizes of O(n2 / 3).
#include <bits/stdc++.h>
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define forn(i, n) fore(i, 0, n)
#define all(a) (a).begin(), (a).end()
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define mp make_pair
#define pb push_back
#define x first
#define y second
using namespace std;
template<class A, class B> ostream& operator << (ostream &out, const pair<A, B> &p) {
return out << "(" << p.first << ", " << p.second << ")";
}
template<class A> ostream& operator << (ostream &out, const vector<A> &v) {
out << "[";
forn(i, sz(v)) {
if(i > 0)
out << " ";
out << v[i];
}
return out << "]";
}
mt19937 myRand(time(NULL));
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
inline int gett() {
return clock() * 1000 / CLOCKS_PER_SEC;
}
const ld EPS = 1e-9;
const int INF = int(1e9);
const li INF64 = li(INF) * INF;
const ld PI = 3.1415926535897932384626433832795;
const int N = 100 * 1000 + 555;
int n, m, aa[N], a[N];
int qt[N], qx[N], qy[N];
inline bool read() {
if(!(cin >> n >> m))
return false;
forn(i, n)
assert(scanf("%d", &aa[i]) == 1);
forn(i, m) {
assert(scanf("%d%d%d", &qt[i], &qx[i], &qy[i]) == 3);
qx[i]--;
}
return true;
}
vector<int> vars[4 * N];
vector<li> f[4 * N];
li sumAll[4 * N];
inline void addValF(int k, int pos, int val) {
sumAll[k] += val;
for(; pos < sz(f[k]); pos |= pos + 1)
f[k][pos] += val;
}
inline li sum(int k, int pos) {
li ans = 0;
for(; pos >= 0; pos = (pos & (pos + 1)) - 1)
ans += f[k][pos];
return ans;
}
inline li getSumF(int k, int pos) {
return sumAll[k] - sum(k, pos - 1);
}
li getSumST(int v, int l, int r, int lf, int rg, int val) {
if(l >= r || lf >= rg)
return 0;
if(l == lf && r == rg) {
int pos = int(lower_bound(all(vars[v]), val) - vars[v].begin());
return getSumF(v, pos);
}
int mid = (l + r) >> 1;
li ans = 0;
if(lf < mid)
ans += getSumST(2 * v + 1, l, mid, lf, min(mid, rg), val);
if(rg > mid)
ans += getSumST(2 * v + 2, mid, r, max(lf, mid), rg, val);
return ans;
}
void addValST(int k, int v, int l, int r, int pos, int pos2, int val) {
if(l >= r)
return;
if(!k)
vars[v].pb(pos2);
else {
int cpos = int(lower_bound(all(vars[v]), pos2) - vars[v].begin());
addValF(v, cpos, val);
}
if(l + 1 == r) {
assert(l == pos);
return;
}
int mid = (l + r) >> 1;
if(pos < mid)
addValST(k, 2 * v + 1, l, mid, pos, pos2, val);
else
addValST(k, 2 * v + 2, mid, r, pos, pos2, val);
}
int pr[N];
set<int> ids[N];
void build(int k, int v, int l, int r) {
fore(i, l, r)
if(!k)
vars[v].pb(pr[i]);
else {
int pos = int(lower_bound(all(vars[v]), pr[i]) - vars[v].begin());
addValF(v, pos, i - pr[i]);
}
if(l + 1 == r)
return;
int mid = (l + r) >> 1;
build(k, 2 * v + 1, l, mid);
build(k, 2 * v + 2, mid, r);
}
inline void eraseSets(int k, int pos) {
addValST(k, 0, 0, n, pos, pr[pos], -(pos - pr[pos]));
ids[ a[pos] ].erase(pos);
auto it2 = ids[ a[pos] ].lower_bound(pos);
if(it2 != ids[ a[pos] ].end()) {
int np = *it2;
assert(a[np] == a[pos]);
assert(pr[np] == pos);
addValST(k, 0, 0, n, np, pr[np], -(np - pr[np]));
pr[np] = pr[pos];
addValST(k, 0, 0, n, np, pr[np], +(np - pr[np]));
}
a[pos] = -1;
pr[pos] = -1;
}
inline void insertSets(int k, int pos, int nval) {
auto it2 = ids[nval].lower_bound(pos);
assert(it2 == ids[nval].end() || *it2 > pos);
if(it2 != ids[nval].end()) {
int np = *it2;
assert(a[np] == nval);
addValST(k, 0, 0, n, np, pr[np], -(np - pr[np]));
pr[np] = pos;
addValST(k, 0, 0, n, np, pr[np], +(np - pr[np]));
}
pr[pos] = -1;
if(it2 != ids[nval].begin()) {
auto it1 = it2; it1--;
assert(*it1 < pos);
pr[pos] = *it1;
}
addValST(k, 0, 0, n, pos, pr[pos], +(pos - pr[pos]));
ids[nval].insert(pos);
a[pos] = nval;
}
inline void precalc() {
forn(v, 4 * N) {
sort(all(vars[v]));
vars[v].erase(unique(all(vars[v])), vars[v].end());
f[v].assign(sz(vars[v]), 0);
sumAll[v] = 0;
}
}
inline void solve() {
forn(k, 2) {
if(k) precalc();
forn(i, N)
ids[i].clear();
forn(i, n)
a[i] = aa[i];
vector<int> ls(n + 1, -1);
forn(i, n) {
pr[i] = ls[ a[i] ];
ls[ a[i] ] = i;
ids[ a[i] ].insert(i);
}
build(k, 0, 0, n);
// cerr << k << " " << clock() << endl;
forn(q, m) {
if(qt[q] == 1) {
eraseSets(k, qx[q]);
insertSets(k, qx[q], qy[q]);
} else
if(k) printf("%I64d\n", getSumST(0, 0, n, qx[q], qy[q], qx[q]));
}
// cerr << k << " " << clock() << endl;
}
}
int main(){
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
int t = gett();
#endif
srand(time(NULL));
cout << fixed << setprecision(10);
while(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << gett() - t << endl;
t = gett();
#endif
}
return 0;
}
848D - Shake It!
by cyand1317
Use DP. f[i][j] keeps the number of subgraphs with i operations and a minimum cut of j. The transition may be in a knapsack-like manner. Add more functions (say another g[i][j]) if needed to make it faster.
There are more than one way to do DP, you can also read about other nice solutions here and here.
#include <cstdio>
#include <cstring>
typedef long long int64;
static const int MAXN = 53;
static const int MODULUS = 1e9 + 7;
#define _ % MODULUS
#define __ %= MODULUS
int n, m;
// f[# of operations][mincut] -- total number of graphs
// g[# of operations][mincut] -- number of ordered pairs of two graphs
int64 f[MAXN][MAXN] = {{ 0 }}, g[MAXN][MAXN] = {{ 0 }};
int64 h[MAXN][MAXN];
inline int64 qpow(int64 base, int exp) {
int64 ans = 1;
for (; exp; exp >>= 1, (base *= base)__) if (exp & 1) (ans *= base)__;
return ans;
}
int64 inv[MAXN];
int main()
{
for (int i = 0; i < MAXN; ++i) inv[i] = qpow(i, MODULUS - 2);
scanf("%d%d", &n, &m);
f[0][1] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i + 1; ++j) {
// Calculate g[i][*]
// pair(i)(j) = graph(p)(r) in series with graph(q)(s)
// where p+q == i-1, min(r, s) == j
for (int p = 0; p <= i - 1; ++p) {
int q = i - 1 - p;
for (int r = j; r <= p + 1; ++r)
(g[i][j] += (int64)f[p][r] * f[q][j])__;
for (int s = j + 1; s <= q + 1; ++s)
(g[i][j] += (int64)f[p][j] * f[q][s])__;
}
// Update all f with g[i][*]
// Iterate over the number of times pair(i)(j) is appended in parallel, let it be t
// h is used as a temporary array
memset(h, 0, sizeof h);
for (int p = 0; p <= n; ++p)
for (int q = 1; q <= p + 1; ++q) {
int64 comb = 1;
for (int t = 1; p + t * i <= n; ++t) {
comb = comb * (g[i][j] + t - 1)_ * inv[t]_;
(h[p + t * i][q + t * j] += f[p][q] * comb)__;
}
}
for (int p = 0; p <= n; ++p)
for (int q = 1; q <= p + 1; ++q)
(f[p][q] += h[p][q])__;
}
}
printf("%lld\n", f[n][m]);
return 0;
}
848E - Days of Floral Colours
by cyand1317
Break the circle down into semicircles. Then there will be 1D/1D recurrences over several functions.
Use FFT in a divide-and-conquer manner to optimize it.
#include <cstdio>
typedef long long int64;
static const int MAXN = 50004;
static const int MODULUS = 998244353;
#define _ % MODULUS
#define __ %= MODULUS
int n;
int64 g[MAXN];
int64 f0[MAXN], f1[MAXN], f2[MAXN];
int main()
{
scanf("%d", &n);
g[0] = 1;
g[2] = 1;
for (int i = 4; i <= n; i += 2) g[i] = (g[i - 4] + g[i - 2])_;
f0[0] = 0;
f1[0] = 1;
f2[0] = 4;
for (int i = 1; i <= n; ++i) {
f0[i] = g[i] * i _ * i _;
for (int j = 1; j <= i - 2; ++j) {
f0[i] += g[j] * j _ * j _ * f0[i - j - 1]_;
f0[i] += g[j - 1] * j _ * j _ * f1[i - j - 2]_;
}
f1[i] = g[i] * (i + 1)_ * (i + 1)_ + f0[i - 1];
for (int j = 1; j <= i - 2; ++j) {
f1[i] += g[j] * (j + 1)_ * (j + 1)_ * f0[i - j - 1]_;
f1[i] += g[j - 1] * (j + 1)_ * (j + 1)_ * f1[i - j - 2]_;
}
f0[i]__; f1[i]__;
}
for (int i = 1; i <= n; ++i) {
f2[i] = g[i] * (i + 2)_ * (i + 2)_ + f1[i - 1];
for (int j = 1; j <= i - 1; ++j) {
f2[i] += g[j] * (j + 1)_ * (j + 1)_ * f1[i - j - 1]_;
f2[i] += g[j - 1] * (j + 1)_ * (j + 1)_ * f2[i - j - 2]_;
}
f2[i]__;
}
int64 ans = 0;
ans += (g[n - 1] + g[n - 3]) * (n - 1)_ * (n - 1)_ * n _;
for (int i = 2; i <= n - 2; ++i) {
ans += g[i - 1] * (i - 1)_ * (i - 1)_ * f0[n - i - 1]_ * i _;
ans += g[i - 2] * (i - 1)_ * (i - 1)_ * f1[n - i - 2]_ * 2 * i _;
if (i >= 3 && i <= n - 3)
ans += g[i - 3] * (i - 1)_ * (i - 1)_ * f2[n - i - 3]_ * i _;
}
printf("%lld\n", ans _);
return 0;
}
#include <cstdio>
#include <cstring>
typedef long long int64;
static const int LOGN = 18;
static const int MAXN = 1 << LOGN;
static const int MODULUS = 998244353;
static const int PRIMITIVE = 2192;
#define _ % MODULUS
#define __ %= MODULUS
template <typename T> inline void swap(T &a, T &b) { static T t; t = a; a = b; b = t; }
int n;
int64 g[MAXN];
int64 g0[MAXN], g1[MAXN], g2[MAXN];
int64 f0[MAXN], f1[MAXN], f2[MAXN];
int64 q0[MAXN], q1[MAXN];
int64 t1[MAXN], t2[MAXN], t3[MAXN], t4[MAXN];
inline int qpow(int64 base, int exp)
{
int64 ans = 1;
for (; exp; exp >>= 1) { if (exp & 1) (ans *= base)__; (base *= base)__; }
return ans;
}
int bitrev[LOGN][MAXN];
int root[2][LOGN];
inline void fft(int n, int64 *a, int direction)
{
int s = __builtin_ctz(n);
int64 u, v, r, w;
for (int i = 0; i < n; ++i) if (i < bitrev[s][i]) swap(a[i], a[bitrev[s][i]]);
for (int i = 1; i <= n; i <<= 1)
for (int j = 0; j < n; j += i) {
r = root[direction == -1][__builtin_ctz(i)];
w = 1;
for (int k = j; k < j + (i >> 1); ++k) {
u = a[k];
v = (a[k + (i >> 1)] * w)_;
a[k] = (u + v)_;
a[k + (i >> 1)] = (u - v + MODULUS)_;
w = (w * r)_;
}
}
}
inline void convolve(int n, int64 *a, int64 *b, int64 *c)
{
static int64 a1[MAXN], b1[MAXN];
memcpy(a1, a, n * 2 * sizeof(int64));
memcpy(b1, b, n * 2 * sizeof(int64));
memset(a + n, 0, n * sizeof(int64));
memset(b + n, 0, n * sizeof(int64));
fft(n * 2, a, +1);
fft(n * 2, b, +1);
int64 q = qpow(n * 2, MODULUS - 2);
for (int i = 0; i < n * 2; ++i) c[i] = a[i] * b[i]_;
fft(n * 2, c, -1);
for (int i = 0; i < n; ++i) c[i] = c[i] * q _;
memcpy(a, a1, n * 2 * sizeof(int64));
memcpy(b, b1, n * 2 * sizeof(int64));
}
// Calcukates f0 and f1.
void solve_1(int l, int r)
{
if (l == r) {
(f0[l] += g0[l])__;
(f1[l] += g1[l])__;
return;
}
int m = (l + r) >> 1;
solve_1(l, m);
int len = 1;
while (len < r - l + 1) len <<= 1;
for (int i = 0; i < len; ++i) q0[i] = (i + l <= m ? f0[i + l] : 0);
for (int i = 0; i < len; ++i) q1[i] = (i + l <= m ? f1[i + l] : 0);
for (int i = len; i < len * 2; ++i) q0[i] = q1[i] = 0;
convolve(len, g0, q0, t1);
convolve(len, g1, q0, t2);
convolve(len, g1, q1, t3);
convolve(len, g2, q1, t4);
for (int i = 0; i < len; ++i) {
if (i + l >= m + 1 - 1 && i + l <= r - 1) {
(f0[i + l + 1] += t1[i])__;
(f1[i + l + 1] += t2[i])__;
}
if (i + l >= m + 1 - 3 && i + l <= r - 3) {
(f0[i + l + 3] += t3[i])__;
(f1[i + l + 3] += t4[i])__;
}
}
solve_1(m + 1, r);
}
// Calculates f2.
void solve_2(int l, int r)
{
if (l == r) {
(f2[l] += (g2[l] + (l >= 1 ? t1[l - 1] : 0)))__;
return;
}
int m = (l + r) >> 1;
solve_2(l, m);
int len = 1;
while (len < r - l + 1) len <<= 1;
for (int i = 0; i < len; ++i) q0[i] = (i + l <= m ? f2[i + l] : 0);
for (int i = len; i < len * 2; ++i) q0[i] = 0;
convolve(len, g2, q0, t2);
for (int i = 0; i < len; ++i) {
if (i + l >= m + 1 - 3 && i + l <= r - 3) {
(f2[i + l + 3] += t2[i])__;
}
}
solve_2(m + 1, r);
}
int main()
{
for (int s = 0; s < LOGN; ++s)
for (int i = 0; i < (1 << s); ++i)
bitrev[s][i] = (bitrev[s][i >> 1] >> 1) | ((i & 1) << (s - 1));
for (int i = 0; i < LOGN; ++i) {
root[0][i] = qpow(PRIMITIVE, MAXN >> i);
root[1][i] = qpow(PRIMITIVE, MAXN - (MAXN >> i));
}
scanf("%d", &n);
g[0] = 1;
g[2] = 1;
for (int i = 4; i <= n; i += 2) g[i] = (g[i - 4] + g[i - 2])_;
for (int i = 0; i <= n; ++i) {
g0[i] = g[i] * i _ * i _;
g1[i] = g[i] * (i + 1)_ * (i + 1)_;
g2[i] = g[i] * (i + 2)_ * (i + 2)_;
}
solve_1(0, n);
int len = 1;
while (len < n) len <<= 1;
convolve(len, g1, f1, t1);
solve_2(0, n);
int64 ans = 0;
ans += (g[n - 1] + g[n - 3]) * (n - 1)_ * (n - 1)_ * n _;
for (int i = 2; i <= n - 2; ++i) {
ans += g0[i - 1] * f0[n - i - 1]_ * i _;
ans += g1[i - 2] * f1[n - i - 2]_ * 2 * i _;
if (i >= 3 && i <= n - 3)
ans += g2[i - 3] * f2[n - i - 3]_ * i _;
}
printf("%lld\n", ans _);
return 0;
}
Behind the scene and random things (read if tired of problemsolving)
Perhaps some may have noticed that at the end of editorial of #418 it's written that
Probably it will be for Ha...
Yes, I had had ideas for the last four problems for Div. 2 by that time. Then I came up with Div. 2 A when lying on bed one night, seems I underestimated its trickiness :/
(1 September 2017 is also when the story of Harry Potter ends, so to me seems like a great coincidence?)
After my unsuccessful performance at the National Olympiad (that's another thing to talk about), on that evening when everything seemed dull, I changed Div. 1 E to what it looks like now — it used to be Div. 1 C or so. "I'm poor at problemsolving. This is the hardest I can come up with," I thought, "and if it doesn't qualify then I'd better give up on holding a round with Div. 1."
Then in early August I created the proposal with all problems. After it was reviewed, some of them were changed, moved or replaced, and I ended up having no Div. 1 D. I had an idea and put it to Div. 1 D, but we had difficulty distinguishing different complexities, so it was set aside and replaced with the problem from adedalic. Schoolwork kept disrupting me from working on preparation, but I managed to allocate time to do it all for my own problems (except tutorials, :P). adedalic's problem is prepared by him and KAN, thank you!
Then two hours before the contest, it was suggested that swapping Div. 1 C and Div. 1 D would be good. I had't had enough time to test the new problem myself, but I thought the second division may prefer data structures to multidimensional DP and agreed. Then Div. 1 contestants jump from A to C and had unfavourable luck... My sympathy, hope you have enjoyed the problems themselves.
These are random fragments of the story behind this round. It wouldn't have been possible without you, dear contestants and members of the community. My deep gratitude!
Also, the problems feature songs created by songwriters and the voice of Hatsune Miku. Let it be happy or sad, separation or reunion, the problems are all inspired by the songs at the very beginning (not necessarily contents though, for example 2A and 1E are just related to the songs in title). Here's the list if you're interested.
- ODDS&ENDS by ryo
- Tell Your World by kz
- from Y to Y by OneRoom
- Rooter's Song by DECO*27
- Sayonara Souvenir (Goodbye Souvenir) by Toa
- shake it! by emon(Tes.)
- Hanairo Biyori (Flower Colored Weather) by Natsume Chiaki
Thank you for reading. Next round? Perhaps something more traditional, who knows? Believe me, I'll try harder if this happens.
Cheers! \(^ ^)/
UPD Packages for problems are uploaded. They are in Polygon format and contain everything including statements, tests & generators, validators & checkers, and solutions. You can download them from Google Drive or Baidu Drive.











No hints for div 1 C?
I would hardly call it editorial...
He said in the statement "Detailed tutorials will be available later."
Though I don't really understand, why isn't the editorial done before the contest. Why schedule the contest, before the editorial is finished?
Ah, I missed that it is not its final form.
"Editorials" originated as things like commentary, related discussions etc. The tutorials are not fully ready by now but I think quick hints may help some. Thank you for your patience.
When someone gets too famous for the super tricky problems in his contest
Having real tutorials would be nice. That way we could understand what the code is based on. For example what is the idea behind 848A?
First add same characters together. If you add n characters, the cost will be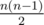 . Though I can't prove there can't be a better cost, you can achieve it by adding the letters one another, so you have costs 1, 2, 3, ..., n which summarized results in the formula.
. Though I can't prove there can't be a better cost, you can achieve it by adding the letters one another, so you have costs 1, 2, 3, ..., n which summarized results in the formula.
Secondly you add same character groups together for 0 cost.
For a given k you can always greedily take the highest x which for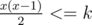 , add x same characters, and deduct
, add x same characters, and deduct 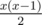 from k. Repeating this process will result in a correct answer.
from k. Repeating this process will result in a correct answer.
It is actually not hard to prove that this is minimal. We claim that if the letter i appears cnt[i] times in the string, the cost needed to concatenate all the strings will always be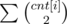 .
.
Consider any pair of letter in the string. If they're different, they will not contribute to the cost. If they're the same, the moment the string containing the first letter is concatenated with the string containing the second letter, this pair will contribute 1 to the total cost. Other than that, this pair will not contribute to the cost. Thus, the total cost is just the number of unordered pairs of same letters.
how do you prove the greedy algorithm is correct?
Why can we greedily deduct? I did it like given n coins make a sum m but that was obviously an overkill. How to prove that we can use greedy for this one.
When you concatenate 2 strings the cost is the number of pairs (from the first string, from the second string) for each letter so the total cost is the number of pairs for each letter because each pair will be counted once.
The greedy outputs a string of O(sqrt(n)) length.
We can take a maximum of 26 letters right? So what I did was dynamic programming to find which elements (taken any numbers of time) of the set {1,3,6,10,15,21..} will add up to k. But subtracting the maximum number less than equal to k also works. I couldn't prove that the number of characters used will be less than equal 26. How to do that?
You might need to take more than 26 letters... Starting from 26 * 25 / 2 + 1 in fact you need strictly more than 26 letters.
Edit: if you meant letters as in 'a' to 'z', as I said the output is O(sqrt(n)) so it's easily less than the limit.
Thank you!
We work backwards greedily by taking the maximal element in the set you described and subtracting it from n at every step. Then worst case n is one less than an element in the set, or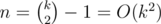 for some k. Then
for some k. Then 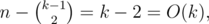 so after each operation, we get at most the square root of what we started with. Now it should be clear that 26 letters are more than enough, since n(1 / 2)26 < < 1 + ε where n = 105.
so after each operation, we get at most the square root of what we started with. Now it should be clear that 26 letters are more than enough, since n(1 / 2)26 < < 1 + ε where n = 105.
Ok got it. Thank you very much! I did an overkill by using dp there :(
I also use the dp solution, but could you please explain why the greedy algorithm is correct?
Nice!
how do you prove the greedy algorithm is correct?
Each letter you use, transform n into O(sqrt(n)). That converges faster to 1 than dividing by 2 (that would be O(logn) letters needed) so there are enough letters.
thank you
Cost of adding n characters always is n * (n — 1) / 2. I prove it like this: Lets say cost of adding n characters is f(n), then: f(n) = f(x) + f(y) + x * y, such x + y = n. By induction if f(x) = x * (x — 1) / 2 and f(y) = y * (y — 1) / 2, then f(n) = n * (n — 1) / 2.
I think this is a really nice and neat proof. I have never thought about using induction to prove this conclusion. Thanks a lot for sharing such a nice idea.
You're welcome. Also there is another proof that I really like it.
Consider a graph with n vertex and no edges at first (for each character we consider a vertex). Each time we merge x characters to y characters, that mean we connect edges between those x vertex to those y one. And our cost is equal to the number of edges we draw (x * y).
At the end the graph is complete and the total cost is equal to number of edges of a complete graph with n vertex which is n * (n — 1) / 2.
:)
actually Gauss prove that every natural number is written as at most 3 triangular numbers
Div2B can be solved with randomized algorithm. You need to choose two points randomly and check if the line going through these points can be one of these two lines which we are looking for. All you have to do now is repeat this about 100 times and you can be 99.999...% sure that if answer is "Yes" you found it at least once.
Did anyone get AC using this method?
When we have 3 leftmost points there must be a line which is going through 2 of those points.
Yep , got accepted . Thanks for the idea .
Submission
could not even solve A. i want to kill myself.
Hello, the solution to this problem was kept on this. Think about it. If you want, I can explain 29975733
Do not worry. As you practice more, you will do better. Trust yourself!
Can anyone please provide a more detailed explanation for div 2 D?
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Is it editorial or just solution codes?
Detailed tutorials will be available later.
Div2B. What if all of these 3 points are lying on 1 correct line?
Then answer will be No.
like (1, 1), (2, 2), (3, 3), (4, 5), (5, 6). Why no??
it's yes
You asked "What if all of these 3 points are lying on 1 correct line?" the case of only 3 points.
doesn't matter , because we are searching the set of points which doesn't belong to that line in the solution above marked with visited[i] =false; if no points found then no; if one point found then yes; else we check the rest of points belongs to the same line and it's parallel to the first one
The first idea works without modification.
You will check the same line three times, which will find the solution if the answer is Yes, and fail otherwise, because there must be one line passing through all three points in this case.
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Did anyone got accepted Div.1 C using sqrt query caching? i.e. blocking queries into sqrt blocks and solving the problem for each block. Time complexity of my solution is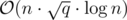 but my solution got failed (TLE).
but my solution got failed (TLE).
My solution with same time complexity passed(29992066).
My solution is exactly the same as yours... I think the problem is I used too many vectors.
Could someone explain the solution to div2B? (29992706)
you need to find out is there exisit two lines
y = ax + b1 and y = ax + b2
such that every points on it, and each line should have at least one point, so you could check for three cases:
(just like Tommyr7's solution (first idea) above)
and 29992706 just try to find out if there exist b1 and b2, by counting 2b
y = ax + b
2y = 2ax + 2b
2b = 2y - 2ax
when you find a,b when, for example: y=7 5 8 6 9 so we have x= 1,2,3,4,5 what will you do with your function: y=ax+b ?
y=ax+b is a form of line, so if you got a, b, then you got a line
thank you, btw, please answer me what is the main idea of Tommyr7's solution ?
I think the main idea of Tommyr7's solution is that there only have 3 cases, just the same as what I've said above.
When I don't believe that div2 A is solving in so simple way and write dp :D
I know that feeling :D 29975756
I know i'm not the only one :)
The problems were good yesterday. I was only able to solve only the first problem, but I got some satisfaction upon being able to solve it. It wasn't purely implementation-based, but also needed a good observation.
Overall,
I appreciate the writers of this contest for these points. However, it is difficult to understand for a beginner. Some more explanation would be good.
Div2D:
Dancers in the same group will move on the same x + y line (a line of slope - 1), and however collisions take place, they will keep current relative order of x and y.
What does this mean? What is an x+y line?
Their coordinates will always have the same x + y during movement. If A and B have the same x + y, and xA ≤ xB holds at the beginning, it will hold throughout the whole process.
Div2B In the first approach, " ans|=check(1.0*(a[3]-a[2]),a[2]*2-a[3]); " I cannot make the sense out of putting a[2]*2-a[3] in the second argument. In the check function, author has assumed the starting point to be 1. Ugh not making any sense to me, someone please explain!
The b argument is the interception of the line. With the third case it should be a2 - (a3 - a2) = 2a2 - a3.
really wonderful tutorial !
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
It would take a few minutes for the tutorial to get from Polygon to CF, stay tuned.
in question A how can u say if n is odd and a[0] and a[n-1] is "only case" where answer is yes.there may be some other cases......
If a valid way exists, then n, a1 and an are odd.
If n, a1 and an are odd, then a valid way exists.
So this condition is necessary and sufficient.
can you prove if n is odd or even and a[n-1] is not odd there cannot exist odd number of subsets[problem:849A]
The answer is No not because of this. It's because if the last element is even, in every possible way to divide the sequence we'll have a segment that doesn't end with an odd number, which makes the whole division invalid.
what if n is even and a[n-1] is odd.Thanks in advance.
For an odd number of segments of odd length each, the sum of their lengths has to be odd (say, sum of three odd numbers is odd, sum of five odd numbers is odd etc.). So for an even n there is no solution.
what if we have a sequence like 0 1 0? we can still get segment {1} which is odd?
The entire sequence need to be divided, and all resulting subsegments should meet the requirement.
In your case there will be two more subsegments consisting of only one element 0, which are invalid.
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
Div2 D What is the custom sort doing. My implementation required a vector of tuple and two more 2D vectors of pair of ints. Can you explain what is happening in your sort. I cannot follow through.
Also a general question, I have a hard time reading and understanding other's code. Any suggestions on how you approach it?
For each x + y group, before everything starts, go down the left border of the stage and go rightwards along the bottom, record the order in which you meet dancers in it.
After everything finishes, go rightwards along the top and then go down the right border and record the order. These two orders will be the same because they're actually sorting the dancers by their order from top-left to bottom-right, that is, "initial x values" (after moving them backwards in the first place) in the tutorial.
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
How to do 849B — Tell Your World if number of lines is a variable ?
Let this number be m.
Use the second idea from the tutorial. But instead we should iterate over a pair of points which is on the same line, and find out the slope k.
Then we need to check whether all the points can be connected with m lines of slope k. For each point (i, yi), we calculate the interception bi = yi - i × k. Find out how many different bi's are there, and if this equals m, then the answer is Yes.
This works in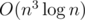 if sorting or
if sorting or
std::setis used, or O(n3) if hash tables are used. I wonder whether a better solution exists.Thanks for the variation, I find it interesting :)
I set a more advanced version of this problem for CS Academy this summer, feel free to try it:
https://csacademy.com/contest/round-38/task/parallel-lines/statement/
Great, thank you!
Great! Thanks both of you!
Found a test case for Div2 B but Can not find why the answer should be "YES"
Test case:
4
5 7 11 17
Any help would be appreciated .
is div 2 B test case 13 wrong?
5
-954618456 -522919664 -248330428 -130850748 300848044
try excel scatter chart
Grade outputs yes, but I don't think so
I don't understand how to build the segtree for div1C — How should the tree handle the b.first >= l condition while the segment [l,r] remains as a continuous segment?
After dividing query on log to some nodes of segtree they transform to "get sum value of all b.first >= l from all elements which are controlled by fixed node", so if you sort all b.first in fixed node you get query on suffix.
Thanks for the details, now I get it. I've never thought of building the tree in this way before, I was stucked with having a fixed size node simliar to 2D BIT... =P
How to take care of updates?
Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
I don't understand Div2D/Div1B , so can anyone help me to explain this problem more clealy ? (sorry for my poor English :((( )
Tutorial for 848B-Rooter's Song
Two points in the second paragraph, maybe it shall be...?
(xi-ti, 0) -> (xi, -ti)
(0, yi-ti) -> (-ti, yi)
Anyone who knows how to solve div1.C by Wavelet Tree?
I have got a better algorithm on div1.E.
At first we get a recursion, just like what the tutorial says.
Let g0(x) = g(x) * x2, g1(x) = g(x) * (x + 1)2, g2(x) = g(x) * (x + 2)2.
Then we use the generated function of sequence g0, g1 and g2,
as well as sequence f0, f1 and f2
Then we get equations below.
F0(x) = G0(x) + G0(x)F0(x)x + G1(x)F1(x)x3
F1(x) = G1(x) + G1(x)F0(x)x + G2(x)F1(x)x3
F2(x) = G2(x) + G1(x)F1(x)x + G2(x)F2(x)x3
Solve it, we get
We just need to calculate the first n+1 numbers of sequence f0, f1 and f2, so we can solve the equations modulo xn + 1,
The complexity is just O(nlogn), better than the algorithm mentioned above.
Here is my code.
How do you solve the equations?
The equations are all linear! Just like guass' algorithm, function G0(x), G1(x), G2(x) are all constants. At first we solve the previous two equations, we got F0(x) and F1(x), then there is F2(x).
I had thought of solving the problem with polynomial multiplicative inverse, but due to my lack of familiarity with it, I kept the current constraints and the model solution. (Apparently I have a weak mind > <)
Sorry for necroposting, but kudos! It's great to see a solution more elegant than the original one.
BM: code
Time complexity: $$$O(16^2 \cdot \log n)$$$
Super cool! My solution was beaten again OvO
Did you prove a finite order of recurrence first or find it through trial-and-error?
It seems that there exist a matrix fast power solution by using these 3 formula(because G0(x)、G1(x)、G2(x)all can be calculated with Linear recursion):
F0(x) = G0(x) + G0(x)F0(x)x + G1(x)F1(x)x3
F1(x) = G1(x) + G1(x)F0(x)x + G2(x)F1(x)x3
F2(x) = G2(x) + G1(x)F1(x)x + G2(x)F2(x)x3
so what BM get in fact is matrix's Characteristic polynomial,then it is proved.
Did anyone got accepted Div.1 C using treap inside each node of segment tree? I am getting TLE with that approach, I expect the time complexity to be O((N+Q)log^2(N))
I know your comment is pretty old, but here is my AC submission of Div1 C using segment tree of treaps 110138332. Hope it helps someone
I have a question for div1E, when calculating the final answer.
ans += g[i — 1] * (i — 1)_ * (i — 1)_ * f0[n — i — 1]_ * i _;
The basic idea of counting rotations without duplication is multiplying (i-1) if the second opposite pair appears at index i. However I thought this could lead to counting one answer multiple times. For example, consider n=9 (18 flowers) with opposite pairs of (1,10),(4,13),(8,17) This would be counted 3 times because the second opposite pair appears at index 4. However if you rotate two units, it becomes arrangement with opposite pairs of (1,10),(3,12),(6,15) which will also be counted because its second opposite pair appears at index 3.
If I misunderstood the solution, can someone help me?
The original arrangement is counted three times: rotated by 0, 1 and 2 units anti-clockwise, respectively. The derivative you mentioned is the original one rotated by 2 units clockwise, hence it's not included in this case but counted in its own case instead.
For Div2 C, this can also be used. Each number can be represented as the sum of 3 triangular numbers. ( A variation of the 3 squares theorem ) Just find 3 squares such that their sum is equal to 8*n+3.
I cannot help expressing my gratitude to the author,especially [Prob.E Shake it].Because the words expressed so clearly and I think the problem gave me much great thoughts.