Привет, всем.
Я решаю одну задачу, и как подзадача требуется организовать рекурсия (возможно, ДП).
Подзадача:
Дано натуральные числа: K, a[1], a[2], .., a[N], где 1<=K<=10^9, 1<=a[i]<=35, 1<=N<=35, sum(a[i])<=35. Требуется разделить эти a[1], a[2], .. , a[N] на несколько не пустых и не пересикающих множества, которые у каждого множества сумма их элементов (НЕ количество, а именно сумма). является делителям число K, конечно, если такое разбиение возможен.
И вот как найти эти множества?
Спасибо.











Есть ссылка на задачу?
Вот эта задача: Timus 2107
Автокомментарий: текст был обновлен пользователем xsc (предыдущая версия, новая версия, сравнить).
Думаю, эта последовательность может помочь.
Спасибо. Мне кажется, Вы предположили, что нужен количество разбиение.
Но в этой задаче не нужен количество разбиение, а нужен быстро найти какой нибуд валидное разбиение, если оно существует, и это задача пренадлежить к Partition of a set, если не ошибаюсь.
Я реализовал очень сложная рекурсия, но это дает TL в 20 тесте.
Нет, я предложил вам подумать над тем, какое отношение это последовательность имеет к задаче. Раз вы не разобрались, дам еще hint: в состоянии важно лишь, сколько из невзятых чисел имеют каждое значение, но неважно, какие именно числа с фиксированным значением были взяты. Поэтому состояний динамики/рекурсии будет ровно столько же, сколько разбиений числа 35 на слагаемые, что в этой последовательности соответствует числу a(35). Переходы же можно делать похожим способом: перебирать x — новое число и его разбиение на слагаемые из свободных еще чисел. Совсем тривиальная оценка времени работы такой динамики — это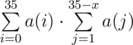 , но на самом деле там будет сильно меньше, если правильно отсекать разбиения, не дающие переход. Но даже такая оценка ограничивает число переходов как 108.
, но на самом деле там будет сильно меньше, если правильно отсекать разбиения, не дающие переход. Но даже такая оценка ограничивает число переходов как 108.
Спасибо, огромное. AC 0.015s!.