Hi!
Thanks to all of you participates, who made this contest possible. And thanks to Lewin and Arterm, also to the great coordinator, Nikolay KAN Kalinin, zemen, WHITE2302, and for sure MikeMirzayanov.
Test data and code solutions. It's the original packages from polygon, you can find pretests, tests, generators, validators, etc in it.
Hints
Div.2 A: Take a look at notes section.
Div.2 B: Create a circle with these points.
Div.1 B: Fix the gcd.
Div.1 C: Tag: Grundy number.
Details
Div.1 C
I want to thank my grand teacher Mojtaba moji FayazBakhsh here. Who was my teacher not only for coding but also a teacher for my life. Thanks Mojtaba! Thanks to you and all of other good teachers in the world.
Solutions
Author: Arpa
Author: Arpa
Author: Lewin
Thanks to Lewin, the writer of this tutorial.
Author: Arpa
Author: Arpa
Author: Arterm
Thanks to WHITE2302, the writer of this tutorial. I translated this tutorial to English.
Author: Arterm
Thanks to Arterm, the writer of this tutorial.
Author: Lewin
Thanks to Lewin, the writer of this tutorial.
I’d like to finish the editorial with the below poem by Hatef Esfahani:
Translation: What can lover (Farhad) do with the power of love? He has no choice but to hurt himself by ax because he feels jealousy to Khosrow. More information about Khosrow and Shirin story.
Good luck and see you soon ;)











Does Arpa know russian language?
no
Do we need to try all posible GCDs in Div2 D ?
Also, how to calculate cnt function efficiently? (number of elements between l and r). Or, we actually dont need to calculate all values, right? We are only interested in which group every ai goes ( group 1 is [0, gcd), group 2 is [gcd, 2*gcd) and so on ) ?
Similarly to how we do sum, we can use a prefixCnt[i] array to represent the count of all numbers less than or equal to i. Thus, cnt(l, r) will be prefixCnt[r] — prefixCnt[l — 1].
Can you explain why f = g — min(g,x/y) ?
If you increase a number by more than x/y to get it to g, you might as well just delete it.
Seems like we should try only prime numbers. It's not necessary to check compounds, because they're multiple of primes. Thus, if we want to know "how many operations of add we need to made our number a[i] to be divided by number G", it will always be less operations if G is some prime, not a compound.
Try this case:
Array elements are: 9 9 9 9 8
Here, we can just increase last element by 1 and get GCD equal to 9 which won't be considered in your approach.
Has anybody got AC on div2C/div1A without using the logic in the editorial and without doing an O(n^3) brute ?
I did in O(n2). Link
Please explain your approach. I can't get the logic from the code. Also , how is your code O(n) ?
Any three points form a triangle. Every triangle has two or three acute angles. So I kept discarding two or three bad points and inserting back the (possibly) good point in the queue, until I had only two possibly good points in the queue. After that, we check if these two remaining points are good in O(n2), comparing with every other pair of points.
This idea is so ingenious!!!, and a lot easier to understand than the intended idea. :))
How do you know for sure that the sum of angles of a triangle in five dimensions is 180 degrees? Is this theorem valid for every dimension? And for that matter how can I be sure that three points form a "triangle" ?
Consider the (2D) plane formed by those points.
Yes, it is true for every Euclidian space. You can see that every triangle defines a plane (maybe not parallel to the axis, but still a plane), and we know that in a plane, it is 180 degrees for sure.
This answers my question guys. It was a nice solution. Got to learn something :D
what are you doing in scalar() function?
dot product.
Thanks @ahmedcpbl
i did it in square
30069050
gud
From given n points, consider 2 points, say A and B with minimum distance (Can be computed in O(n^2) ). Now for any other point C, in triangle ABC, angle ACB will be an acute triangle (as AB is smallest side, angle opposite to it, angle ACB is the smallest, so at max 60 degree). Thus no other point, except for A, B can be good. For A, B. Brute force to check if they are good points or not.
As "AB" is the smallest side, isn't it? However, this approach is that which until now I have not understood any one else, Thank you.
Thanks for mentioning, updated it. Consider any point C, other than A and B.
ABC will form a triangle.
Now what can you comment about the angles in triangle ABC??
We know, angle opposite to the smallest side is the smallest in a triangle. So, angle C, opposite to side AB will be smallest.
In a triangle, we know, ang(A) + ang(B) + ang(C) = 180 deg.
=> ang(C) + ang(C) + ang(C) <= 180 deg. //{{ replacing a variable by another with value less or equal creates an unequality, with lesser towards the replaced one. }}
=> ang(C) <= 60 deg.
Oh Thank you.. I meant that I understood this approach and didn't understand others.
Though, Thank you very much for this extra explanation.
What if more than 1 pair of points has minimum distance? Consider the case where all points form an n-sided regular polygon..
Can someone help me with complexity analysis of Div1C — Arpa and a game with Mojtaba (Grundy Number) ??
I didn't write this solution in the contest because I thought that it will TLE :D
Div2C could be solved just with naive solution
And why do we calculate small number of DP values in Div2E?
Can u please explain how the naive solution passes withing time limit? :O :O
Mine did, it was O(n^3).
It's O(n)
It finds bad points fast because
jandkare always < 11 (see original solution)I understand it now, thanks :)
They break the loops once they find an acute angle. So the worst case is not actually Ω(n3).
Interesting, thanks for the insight :)
For Div2B, why there is no solution when a, b, c are collinear in given order such that dis(a,b) = dis(b,c). Our rotation point is b and rotation angle is 0 deg.
In your case is new position of A same as old position of B...
Yes. Think of a line a-----b-----c such that ab=bc and we move ab over bc.
if u rotate a----b----c about b wont the new line be c---b---a ?
Actually, one can observe that in Div2 C (with n greater than two of course, with the other case being trivial), it is impossible to have more than one good point, and that point must be one of the endpoints of the shortest segment.
Let A and B be good points, and C be another point. Points A,B,C define either a line or a triangle, in both cases there can only be one angle that is not acute.
For the second part, let AB be the shortest segment and C be the good point. Then AB is the shortest edge of triangle ABC, making the angle between AC and BC acute, a contradiction.
Nevermind, got it.
Something that might be good to have in mind:
If you just calculate only for the primes on problem Div1B/Div2D the complexity is O(maxvalue * log(log(maxvalue)))
In the five dimension points problem, isnt there 64 quadrants instead of 10? that is, 2^k instead of 2*k in k-dimension
UPD: I got it now, 2^k is the number of quadrants in k dimention and even though it is a correct upperbound for n in which it is impossible to have a "good" point, 2*k is a still correct and smaller upperbound. Think about a 3 dimensional coordinate system. Put a point in origin. Now try to put as much points as you can so that the origin is a good point. Well, the best you can do is to put points equally espaced by the minimun angle that they need to be good, that is, 90 degrees. So you put one point in every axis, both in positive and negative directions, that is, +x, -x, +y, -y, +z, -z. There are 2*3=6 points, if you put any other point, the origin point will no longer be good. So 2*k+1 is the maximun number of points you can have in k-dimensionso that there can exist a good point
Same here, in the 3-D dimension (0, 0, 0) can be a good point with 8 other points.
I don't understand why quadrants but I thought of it this way.
For current X, if you subtract it from all other vectors, you can consider X to be the origin. What are the maximum number of vectors so that they are pairwise orthogonal? We can use the axes. In 3D, use x, y and z axis. So...the vectors that are orthogonal to each other are (1, 0, 0), (-1, 0, 0), (0, 1, 0), (0, -1, 0), (0, 0, 1), (0, 0, -1). Combinatorially, we see that we can set each coordinate as 1 and -1. In 5D, there are 5 coordinates and each can be set as 1 and -1, so...there are 10 vectors possible such that they are orthogonal in 5D. Am I wrong?
Intuitively we would like to find out the max. size of set of vectors that are orthogonal to each other (or construct this worst case).
The first vector could be chosen arbitarily, and we would always include vector that is the opposite of it (*(-1) to everything), that's 2*1 = 2 vectors for 1 dimension. Because of 180/90 = 2, each time you pick two more vectors on the same plane this effectively reduces the dimension of the room for solution by one (imagine it in 3D and 2D), so the solution is 2*k.
I still say that 2^k is the key of this approach not 2*k, because the number of points follows the number of quadrants.
Fix a point in the origin of a 2D coordinate system. you can put the fore points not on the axis but on the vectors that make angles of 45° with the axis, then you reached to that fore points but by following the quadrants.
The same in a 3D coordinate system, if we draw vectors from the origin and let them make angles of 45° with all axis that are around a current vector then we will obtain 8 vectors that there are angles of 90° between them (which is equal to the number of quadrants, i.e. 2^k). UPD: I have just put a comment under this fixxing what I was wrong in it.
Now I get that we cannot put 8 points in 3D space so the origin point still good point. When we are putting those 8 points inside the quadrants ("inside" them), we will not be able to let any of the vectors from the origin to those points making 45° angles with the axis. But, what we will be able to do is letting vectors' coordinates making 45° angles with the axis, and this isn't what we are searching for.
div2 B: I know that I'm dumb, but why the point around which we rotate the plane and the angle are always exist if ABC is a isosceles triangle?
Where's this point and what's the angle? -_-
You should rotate it about its circumcenter, and the angle will be the angle subtended by AB (or BC) at the center.
My solution for Div1B is different so I thought I'd share. We can basically treat this problem as three different cases. Case 1: x<=y. If x<=y then it is never better to increment a value, so we just find the prime number that is a divisor of the most numbers and the answer is x*(n-(number of given numbers that said prime number is a divisor of)). Case 2: y<x and x<=2y. If this is true then it is never better to increment a value more than once. Let a[i] be the number of given numbers that are divisible by i, and b[i] be the number of given numbers that are one less than a number divisible by i. The answer is then the minimal value of y*b[i]+(n-a[i]-b[i])*x among all prime numbers. Last Case 3: y < x and x > 2y. We know that the answer will be <= n*y because we can increment or not increment every value to make it even. Let's say the gcd we are trying to achieve is a multiple of prime number "p". Let z be ((the number of given numbers p is a divisor of) + (the number of given numbers p is a divisor of if we add 1 to all given numbers)), then when z<n/2 the cost of trying to achieve its gcd would be >= (n/2)*2y which is >= 2ny which we can always achieve. Thus we can brute force checking the minimal cost for all prime numbers that have z>=n/2 (and trying the prime number 2). There are at most 4*log(n) such prime numbers. Thus overall solution is O(N log N).
I got basically the same idea, but failed to note that case 2 exists xd. It's worth adding that this solution has better complexity than one posted in editorial. If we use Rho-Pollard factorization then we are able to solve it on O(n·R0.25) complexity (using typical one we can have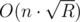 (where R is range of values)
(where R is range of values)
Similar idea, but key point is to check only primes that have z < n/2. Amazing insight! But why are there at most 4*log(n) such prime numbers?
How I get 4*log(n) as an upper bound is we are looking at 2*n numbers (the original n, and n more which are the original n with one added to each of them). Each of these 2*n numbers have at most log(n) distinct prime factors. This gives us 2*n*log(n) primes (with repeats) to use. If we want to find the most primes that could have z>=n/2, we just divide this number by n/2 to get 4*log(n).
3 1 100
1 1 1
answer should be 102.
Why not just remove all 3 for a cost of 3?
Could anyone please provide a proof of problem Div2B?or any link!I couldn't find any proof.Thanks!
What means to move paper around a point? Try to imagine it, or try in real life: it only means to move every point on circle with center in point we are rotating from(origin of rotation). So, that means that point we are looking for must lie on bisector of AB, because both A and its final destination after rotation (which is old B) must be on circle with center in point that we rotate around. Similary, that point must also lie on bisector of BC. But it simply means that that point is circumcenter of ABC. Since angles of rotation must also be same, we have AOB = BOC, which simply means AB = BC. Only thing you need to look out for is collinearity of points A,B,C. I totally forgot that and didnt solve problem in contest.
I think there are some mistakes in the equations in the editorial of Div1B/Div2D. According to the given definitions of letters, shouldn't the implication look like this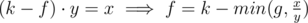 ?
?
Sadly, such mistakes make understanding the tutorial a lot harder or even impossible :/
The Lemma for Div2C/Div1A is also an important lemma for APMO 2017 Problem 5.
See http://artofproblemsolving.com/community/c6h1446917p8273269
I would have saves a lot of time if I remembered this lemma instead of having to derive everything... I'm glad someone else recognizes this, though.
Can someone, please, elaborate on how (and why it works) to build the tournament graph given the list of out degrees of every node in problem D?
No analysis on the maximum number of DP states in the worst case in Div1-C?
When the prime is > 2, the mask is ok (will have no more than 20 first bits).
But when the prime is 2, we can have up to 30 bits in the mask, but we will call the function for this mask with 30 bits only once, and in the recursion this mask will call the function for masks of 29, 28, 27... bits (one of each).
So, with the recursion, the total number of masks with 30 bits is no more than 1, and for 29 bits is no more than 1, and for 28 bits is no more than 2, for 27 no more than 4.. and so on.
So, the total numbers of masks between 30 and 20 bits is no more than 1+1+2+4+8+...+1024. And for the masks between 1 and 20 bits we can compute all states (2^20).
Can anyone explain why the DP in Problem F is t(r) = p / 2 × t(r - 1) + p / 2 × t(r + 1) + r / S but not t(r) = p / 2 × t(r - 1) + p / 2 × t(r + 1) + 1?
Referring to this article (P.4),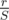 is the probability that hits S before 0.
is the probability that hits S before 0.
Can anyone please explain this in Div2D/Div1B,
Now for each multiple of g like k, let's find the cost of numbers in the range (k - g, k], and sum up these values. We must find the best f and divide the range into two segments (k - g, f] and (f, k] and delete the numbers in the first range and add the numbers in second range till they become k.
We want the numbers in the list to be divisible by g, so we need to increase each number to the nearest number that is a multiple of g. For the numbers in (k-g, f], it's more efficient to delete them instead of incrementing them to equal k. Vice versa for (f, k].
Div2B : Can anybody tell me, what is difference in these codes ? One is accepted, but other one is not.
Accepted code
Failed code
The both solutions got the right answer in custom test, you might want to use
cinandcoutfor double and long long variables, to prevent these weird bugs, also if you're comparing two floating type variables,due to precision errors, its better tofabs(a - b) <= 1e-9or rather thana==b.I got accepted in Div2 D problem. But I don't understand how can we ensure the final number list is non-empty?
Actually, the final list can be empty. I got a WA on test case 106, which goes like this 1 2 3 1 the answer for this case is 2. :) I reviewed the problem, which doesn't mean that a good list should be non-empty.
Thanks, I got it! Bad means non-empty and gcd = 1. So good means empty or gcd > 1.
Arpa Can you please share the proof of complexity in problem Div1C
+1. For someone who knows the Sprague-Grundy theorem, proving the time complexity is the only hard part in the solution :/
in div2 B the given hints is that if the three points cannot form a circle then the answer is NO....but the test case 6 (49152 0 0 0 0 81920 ) answer is NO but we can form a circle using any (a, 0), (0, 0), (0, b) with it's centre at (a/2, b/2).....if i am missing something then please correct me!
the condition that three points should form a circle is necessary but not sufficient, since the objective is to find a rotation than can make A take the place of B and B take the place of C,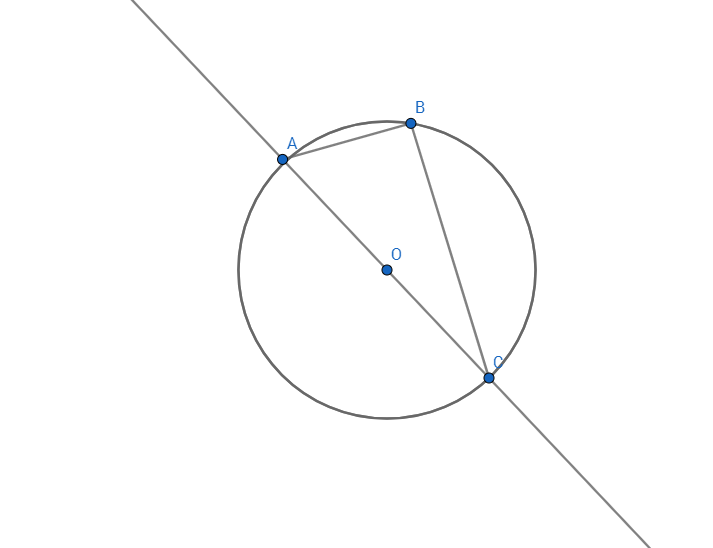 , try rotating the triangle around O, and you will see that's impossible to find such rotation, unless
, try rotating the triangle around O, and you will see that's impossible to find such rotation, unless 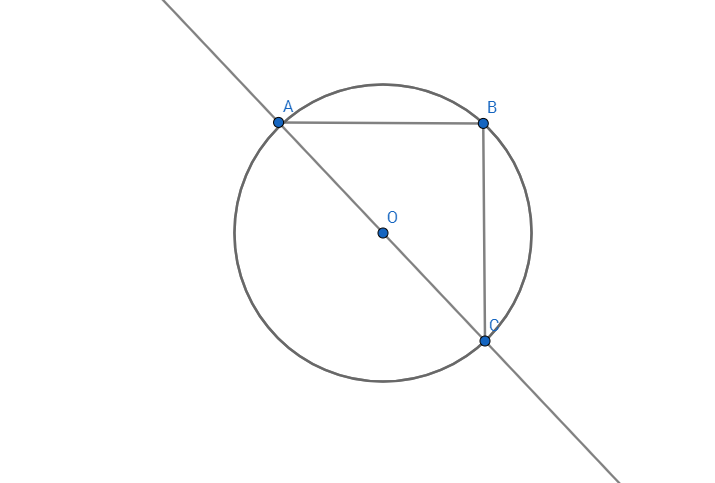 ...
...
Proof of time complexity of Div1C:
Each bitmask has at most 30 bits (because 2^30 < 10^9), and let's think how many bitmasks appears when we calculate grundy number:
If bitmask for prime p has k bits (1<=k<=30), the number of possible bitmasks which has m bits is:
(1<=m<=k/2) at most 2^m (this is obviously true)
(k/2<=m<=k) at most 2^(k-m) (because later 2*m-k bits of m bits never change)
so,the number is at most 2^1+....2^(k/2)+....2^0, which is at most 10^5.
And, there are at most 9*n prime numbers which divides at least one element of a. (because 2*3*...*29>10^9, and 29 is 10-th prime number)
In conclusion, the number of calculation of grundy number must be at most 10^5*9*n <= 9*10^7, and which is too large in relation to the true number, so it works very fast in practice.
Thanks!
The reason why it works well in practice is that only the first few prime numbers can have many bits. Any prime >10 can have at most 8 bits, as 119 > 109.
I am sorry, could you explain this? I cannot see how how $$$11^9 > 10^9$$$ explains your conclusion.
Wouldn't there be 32 quadrants in 5 dimensions?If we put a point (0,0,0,0,0) and other points such that vector between 0 and those points is 45 degree inclined from each axis in each quadrant we can set points such that angle between two vectors are not acute. Hence for 33 points we can get (0,0,0,0,0) as a good point. Correct me if i am wrong.
Hi Lewin!, please, discuss this case.
I also reach to the same idea that is the most number of points which we have to iterate on is 2^k+1 not 2*k+1. UPD: I have just put a comment under this fixxing what I was wrong in it.
Now I get that we cannot put 8 points in 3D space so the origin point still good point. When we are putting those 8 points inside the quadrants ("inside" them), we will not be able to let any of the vectors from the origin to those points making 45° angles with the axis. But, what we will be able to do is letting vectors' coordinates making 45° angles with the axis, and this isn't what we are searching for.
problem B div2: 851B - Arpa and an exam about geometry any 3 non co-linear points could generate a triangle, and any triangle could generate a circle. https://en.wikipedia.org/wiki/Circumscribed_circle and the center of the circle is the intersection point of the triangle medians ,so we now have a circle and we are just need to prove that the angle of rotation between (A,B) equals the angle of rotation between (B,C) let the angle (x) and from the shape below we can see that those two triangles must be identical cause of three equal angles and two equal sides , we just need to check that dis(a,b)==dis(b,c) so that the two angles are equal. sol : http://codeforces.net/contest/851/submission/30098274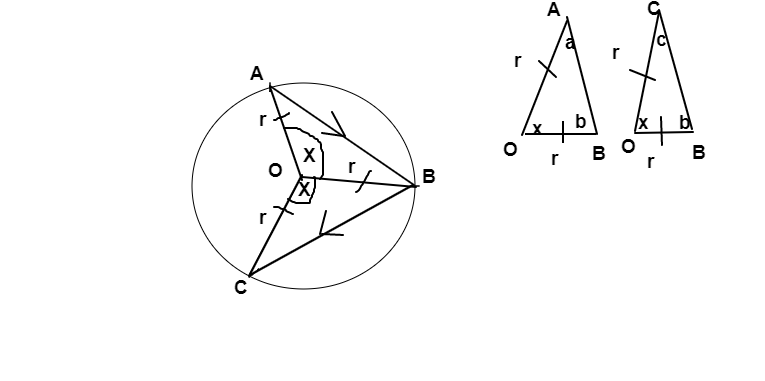
exactly what i was looking for! thanks!!
subham301477845 you're welcome
Thanks for the interesting contest and editorial.
The following is a C++14 main() function of the brute-force algorithm for Problem 851C - Five Dimensional Points:
template< const size_t M, const size_t N > class multi_dimensional_points { .... };
is a generalization of the brute-force algorithm, where the problem is generalized to M-dimensional points, and N is the maximum number of points. The full-implementation is shown in submission 30115750.
Best Regards
Problem E is just a complicated statement combine with a well-known xor convolution.
Can you please share some resources for xor convolution or any boolean convolution? I know how to do polynomial convolution using fft but i can't be able to relate it with any boolean operation.
For problem 850B — Arpa and a list of numbers If the input is: 1 2 6 1 What should the output be? If we delete the only element, then does the gcd exist? Sorry for my poor English.
For 850B — Arpa and a list of numbers. We could solve in this way! Maybe the test data is a little week?
Anyone getting Wrong Answer on test case 40 on Div2 B? I can't see why... Maybe floating point errors?
Floating point could be a possibility. Though this problem can be solved without doubles... Use distance squared and something like cross product to test collinearity.
The following is a c++ solution based on integer numbers only.
30083200
In Div1F, it is possible to find t(r) using a recurrence relation: t(0) = 0,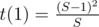 and
and 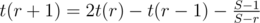 . The first is trivial, the second can be found experimentally, and the third easily follows from
. The first is trivial, the second can be found experimentally, and the third easily follows from 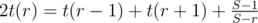 .
.
About Div1D. Does someone prove that there are no "Impossible case" or construct such one?
Can someone explain how to solve div1 E?
by linearity , lets just count the number of cases where a wins over b and c and later multiply it by 3.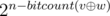
Consider after the voting process , let the 2 vectors we got be v = {v1, v2, v3, ... , vn} and w = {w1, w2, w3, ... , wn} , and if f(v) = f(w) = 1 then this leads to a winning over both. Now for each such pair of vectors , lets count how many ways we can get this.
there are 4 cases
vi = 0 , wi = 0 , then there are 2 ways for the ith voter to give this result
vi = 0 , wi = 1 , there is 1 way
vi = 1 , wi = 0 , there is 1 way
vi = 1 , wi = 1 , there are 2 ways
So the total number of ways for this pair are
Now the we just need to get the number of pairs which have a given xor , this can be done with xor convolution with Fast welsh hadamard transform.
Thanks a lot. Nice explanation.
Hi! Is xor convolution some kind of standard trick? Can you please share some problems which use this technique? Thanks!
I think in problem F it's clearer to let t(r) = E(number of steps taken if we reach S at the end, otherwise 0), then everything that follows makes perfect sense. If we make it conditional on reaching S first, then probabilties of moving to r-1 and r+1 aren't equal and overall it's a bit messier(but still doable).
Anyone find my bug that gets WA on 25 for Div 1 B?
include
include
include
define MAXN 500500
using namespace std; typedef long long ll; vector factors[2*MAXN]; ll c[2*MAXN][3]; ll N, x, y; int a[MAXN]; ll ans, cur; int main() { ans = 1e18; for(int i=2; i<(2*MAXN); i++) { if(factors[i].empty()) { for(int j=1; j<((2*MAXN)/i); j++) { factors[i*j].push_back(i); } } } cin>>N>>x>>y; for(int i=0; i<(2*MAXN); i++) { c[i][2] = N; } for(int i=0; i<N; i++) { cin>>a[i]; for(int j=0; j<factors[a[i]].size(); j++) { c[factors[a[i]][j]][2]--; c[factors[a[i]][j]][0]++; } for(int j=0; j<factors[a[i]+1].size(); j++) { c[factors[a[i]+1][j]][2]--; c[factors[a[i]+1][j]][1]++; } } if(x < y) { for(int i=0; i<(2*MAXN); i++) { ans = min(ans, x*(N-c[i][0])); } } else if(x < (2*y)) { for(int i=0; i<(2*MAXN); i++) { ans = min(ans, y*c[i][1] + x*c[i][2]); } } else { for(int i=0; i<(2*MAXN); i++) { cur = 0; if(c[i][2] <= N/2) { for(int j=0; j<N; j++) { cur += min(x, y*(((i*10000000)-(ll)(a[j]))%i)); } ans = min(ans, cur); } } } cout<<ans<<endl; }
In div2D/div1B,
Now for each multiple of g like k, let's find the cost of numbers in the range (k - g, k], and sum up these values. We must find the best f and divide the range into two segments (k - g, f] and (f, k] and delete the numbers in the first range and add the numbers in second range till they become k. Now to find the best value for f,
(g-f)*y=x/y => f=g-min(g,x/y).How do you get the equation
(g-f)*y=x/y => f=g-min(g,x/y)?what does this mean? Is this some feature of this problem? Can someone explain please,thank you in advance.It must be a typo. See the correction, Comment Link.
Ok,I see.Thank you very much...
Hi, for 850B I simply just brute-forced the top 10 most popular prime factors, can anyone hack this idea or prove why it works?
submission: 74588035
Hi, I know this post is already 3 years ago, but I found the counter test case for your solution,
The correct answer would be 105, but your code result is 108. (the correct gcd in this case is 3, I think any other solution that use certain amount of top prime factor would also have a counter but the counter have to be specific enough.)
Thanks. Added to tests.
I also find another counter test case which results in TLE for this submission 30101518. Here's how to construct it,
n = 470982, x = 1000000000, y = 100, then the input array is a prime number from 3 to 1000000 where each of them repeated 6 times which resulting the array would looks like3 3 3 3 3 3 5 5 5 5 5 5 7 7 7 7 ... 999983 999983.Great. Can you share the generator?
Here is the C++ code that generates that test case.