Добро пожаловать на 2017-2018 ACM-ICPC, NEERC, Southern Subregional Contest, qualification stage (Online Mirror, ACM-ICPC Rules, Teams Preferred).
Этот контест был проведен вчера (17-го сентября). В основном он ориентирован на аудиторию участников из второго дивизиона.
Просьба к официальным участникам: пожалуйста, воздержитесь от участия в онлайн-зеркале, после окончания вы сможете как и все дорешивать задачи.
Во время онлайн-зеркала вы сможете скачать PDF-файлы с условиями (как на русском так и английском языках). Ссылки будут доступны на основной странице соревнования в сайдбаре справа.
Удачи!











Hope it will be rated
Stop daydreaming...
Codeforces is on fire, two days ago MemSql, yesterday Technocup, today neerc and tomorrow one div2 contest!
Where is div2 announcement?
Here.
Удачи всем
Для фиолетовых тоже отлично заходит, на самом деле. Было интересно, крутой контест.
Is it rated?
No
Is there any editorial (official or user) for this round?
Why doesnt you add this kind of Contest to a Programmers Contest log...Please add this feature adding Educational Round and Other contests in a programmers Contest log
How to solve J, L?
J can be solved by binary search on the answer and using max flow to check if it can be done.
For L, notice that in a valid tree, there is an edge between nodes a and b if and only if the sum of the size of a's set containing b and the size of b's set containing a is equal to n. Then once we have all the pairs which must be edges, we check if it forms a valid tree.
Nice solution for L :) I used a different, not so beautiful idea: we can find arbitrary leaf of the tree (and its parent) by looking for set of size 1. After that we can add the edge that we found to the answer and remove given leaf from the tree, moving to the equivalent problem for smaller graph.
J: Binary search the answer. Suppose we have to check if each student can send no more than k gifts. Create a flow with a source s, a sink t, m vertices represent a student pair (pi mean i-th pair) and n vertices on the right (stui mean i-th student). For pair i, create edge (s, pi, 1) and two edges (pi, stuxi, 1), (pi, stuyi, 1). For student i, create edge (stdi, t, min(degi, k)) with degi mean the number of student pair that has student i. Run Dinic max flow algorithm (which work in O(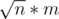 ) due to Karzanov theorem) and check if max flow equal to m.
) due to Karzanov theorem) and check if max flow equal to m.
There's a O(m^2) solution for J without binary search.
http://catalog.lib.kyushu-u.ac.jp/handle/2324/14869/IJFCS-revision.pdf
Exactly! A quick Google search for "orient undirected graph minimize out degree" finds this paper.
In which site can we find the official rank list(not the mirror)?
Official rank list
Official rank list + unofficial commands
How to solve D?
First observation. Let's wait only in the start point. Now to eat the i-th food the dog need to start in any moment from
[t_i — i, T — i -1].
Now we need just count the intersection of maximum number of segments.
Why is it allowed to wait in the start point?
The statement says: "After the show starts the dog immediately begins to run to the right to the first bowl."
Am I missing something?
can you please explain how to find intersection ?
i have tried it but my code failed in test case 121 (:
my approach : i have created pairs and then sort them and just iterate them with the help of two pointers.
my code : http://codeforces.net/contest/847/submission/30774626
I made more than 9 submissions to B, but i keep getting time limit exceeded!! My solution is O(mn) where m is the number of strictly increasing subsequences. Any help? Some people even solved it withing 100 milliseconds :O
when m = n your solution is O(N^2) :)
I made a video explaining my approach to problem k here https://www.youtube.com/watch?v=73s1wyykELQ&feature=youtu.be
A minute of advertisement and half-farewell.
Since 2012 my university (Samara U, previously Samara SAU) has been preparing two big contests in a year:
and
If you are yellow or lower, you may have a nice time solving them.
Now our subregional has an official, approved by Baylor, Qualification contest (this one). So, there won't be qualification contests from my university anymore. We will prepare only one big contest per year, so see you in April or May 2018.
My solution for B, has O(Nlog^2(N)). Why TLE 15? http://codeforces.net/contest/847/submission/30481489
Any hints for E? I think it's supposed to be easy but I'm stuck.
Think about binary search.
First of all, it's not that easy. The fact tourist solves it in 4 minutes doesn't make it easy for a 1800 person. Don't let the standings deceive you.
Binary search the answer, iterate over stars from left to right, try to get the star with the leftmost pacman, consider two ways: 1) go left to the star, then go right, and 2) (tricky!) go right as long as you can, then go left and get the star.
While I was participating in the virtual contest, I was solving some problems solved by fewer people than E, that's why I thought E was supposed to be easy (and why I was punching myself for not getting it). Though it seems like by the end of the contest all 8 problems I solved were ultimately solved by more people than E (E being the first unsolved one in order of number of people which solved it).
Anyway, I thought about binary search but I couldn't figure out how to answer the decision problem for a given time. To be honest, it's still not clear for me from your explanation but I'll try to go from here. Thanks.
Check this problem (solution is in the editorial for CF round 200).
343C — Read Time
Thanks for this!
can you please explain the solution to problem D
Is there any editorial for the problems ?
Will there be an tutorial?
Any hint for Problem B? My code meet TLE on test #27
You can use some data structure like binary search tree to get an O(nlgn) algorithm. In C++, you can use std::set conveniently. Just keep updating the answer queues while iterating the array. Without storing all answer queues, we can use next[] array to record the next item of the current item in the final answer queue. And we use std::set to store the last items of each queues. Then we can use upper_bound to find out the proper queue we should append the new item to.
This is my solution: http://codeforces.net/contest/847/submission/30470282
Thanks, I've just passed this problem. But It doesn't need use std::set, just use vector to score the answer sheet, it must in order actually. Using std::set will cost more when lower_bound moving the iterator.
Some hint for problem D?
Greedily, the answer must happens when the dog waits at the start point for some seconds and then run&eat without waiting. So we just need to try how much time the dog waits at the start point.
Optimize the trivial O(nT) DP solution.
can you please give some hints about the optimization?
How do you make sure in questions like F that there is no edge case left to consider? It just happens to me that after thinking for a hour or two about various conditions, there still remains so many conditions leading to WA. Any help is appreciated. Thanks.
How to solve C?
Guess I am too late but probably might help others.
Let $$$M$$$ be the max possible sum we can generate. Then, $$$M=\frac{N * (N - 1)}{2}$$$. Firstly, if $$$K > M$$$, then ans = "Impossible". Otherwise, we can prove that we can always generate a sum of $$$K$$$.
My observation was this: We can obtain $$$M$$$ by sequentially nesting all brackets. Something like this "(((...)))". We can represent this by a sequence $$$S = 0,1,...,N-1$$$ which corresponds to the nesting values of the opening brackets from left to right. Now let's say we want to make a sum of $$$M-1$$$, what we can do is, simply change the nesting value of the rightmost opening bracket, which is currently $$$N-1$$$ to $$$N-2$$$. So, $$$S = 0,1,...N-2,N-2$$$. Similarly, if we want to make $$$M-2$$$, we can decrease the second last number, which is currently $$$N-2$$$ to $$$N-3$$$. So, $$$S=0,1,...,N-3,N-2$$$. We can regenerate the resulting string from sequence $$$S$$$ by any ad-hoc method.
What we are essentially doing is: every time we want to decrease the sum by $$$1$$$, we decrease the nesting value of the leftmost occurrence of the max nesting value in the sequence $$$S$$$ by 1. Using this pattern you can generate all sums from $$$0$$$ to $$$K$$$. Others might have a more elegant approach, but unfortunately it wasn't discussed.
how to solve e ?