Anyone please elaborate the problem. Thanks in Advance.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 17:32:51 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Let's solve the problem for each prime factor p separately.
Suppose LCM of two numbers i and j has pe in its factorization, then at least one of them must have pe in its factorization as well. There are (e + 1)2 - e2 ways to choose the exponents of p so that one of the numbers has exponent e and the other one has exponent at most e.
First let's make a list of primes with a sieve, then solve the problem for each prime factor as explained above. The results have to be multiplied because each prime factor is independent.
We'll be counting all pairs twice, except the case when i = j (when n is a perfect square), so if the answer calculated is res then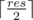 will do the trick.
will do the trick.