shahidul_brur's blog

How to solve this DP on Tree or Centroid Decomposition problem?
By shahidul_brur, 7 years ago, In English

The following problem is from the preliminary contest of ACM-ICPC Dhaka Site 2016.

[Time Limit: 1s and Memory Limit: 1200MB]

Problem Statement:

Given a tree with N( <  = 105) nodes, where value of each node can be either 0 or 1. How many number ways to choose two node where value of these two nodes is 0 and there are exactly two nodes with value equal to 1 on the path from a chosen node to another.

Sample Input:

5 // value of N

0 1 1 0 0 // value of each node, then the below are the edges

1 2

2 3

3 4

4 5

Output:

4

Explanation of Sample Test Case:

You can choose two nodes as (1, 4), (1, 5), (4, 1), (5, 1).

My question is:

  1. How to solve this problem using centroid decomposition?
  2. How to solve this problem using DP?
  • Vote: I like it
  • -1
  • Vote: I do not like it

»
7 years ago, # |
← Rev. 2   Vote: I like it +20 Vote: I do not like it

Use centroid decomposition) If your current centroid — v, and you dfs to u from v, there three case: 1) On path (v,u) there 2 nodes with value 1. Then you want chose any node, which is already dfsed from v, and on path between this node and v there 0 nodes with value 1. 2) On path (v,u) there 1 node with value 1. Then you want chose any node, which is already dfsed from v, and on path between this node and v there 1 node with value 1. 3) On path (v,u) there 0 nodes with value 1. Then you want chose any node, which is already dfsed from v, and on path between this node and v there 2 nodes with value 1.

And sorry for my english)

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

Root the tree at an arbitrary node. Define DP state like this —

dp[u][x] = how many x distance nodes (from u) with value 0 are there in subtree of u

By distance I mean number of 1's in the path. Also note that we don't need to know any answer for x > 2. You can calculate these values easily by a dfs.
So we are done with all chains hanging down. Only thing left is to cross chains.

To combine results, you can divide in two cases —

  • Current node has value 1 — Then you can choose some 1 distance node from a subtree and 0 distance nodes from all other subtree. Or you can choose 0 distance node from a subtree and 1 distance node from all other subtree.

  • Current node has value 0 — Then choose i-distance nodes from one subtree and 2 - i distance nodes from other subtree, .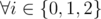

You may need to adjust the final answer, depends on the way you implement it.

→ Reply