bharat.khanna.cse14's blog

Editorial — Manthan Codefest '17
By bharat.khanna.cse14, 7 years ago, In English
Tutorial is loading...
Solution
Tutorial is loading...
DP solution 1
DP solution 2 with minimum and maximum computation
Tutorial is loading...
Solution
Tutorial is loading...
Solution
Tutorial is loading...
Solution
Tutorial is loading...
Solution
Tutorial is loading...
Solution
Tutorial of Manthan, Codefest 17
  • Vote: I like it
  • +26
  • Vote: I do not like it

Comments Comments (52)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Solutions (Code links) are not visible.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem C, if we have node U and it has y children, we need to check every representation of x by y numbers, right? for example, in first childrens subtree we may put 0,1,2,..,x k-labeled nodes, second children can also have 1,2,..., x — a, where a is amount that we used for 1st children and so on. Is this right?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +17 Vote: I do not like it

    Not Necessary. I went into the same dead end during competition lol. From the tutorial, I just figured out we don't need to iterate through all the combinations but instead: Everytime combine the result of two children at a time. All the combinations of these two children are contained in the combined result (from 0 to x). Continue this process till all the children nodes are combined. By this way, it only takes x * x * (number of children) to have the result of all the combinations.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

With problem D. Why does this hold? ~~~~~ For query 1 u v, answer will be "YES" iff u ≠ v (as u is not special case of itself) and lca(u, v) = u. ~~~~~ Should a special case of a part be a special case? Formally, b is a part of a, c is a special case of b, why do we need c to be a special case of a?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    Sorry! There was a mistake in the editorial. All edges in the path from u to v should also be of type "is a special case of"

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it -40 Vote: I do not like it

Third solution for problem B : Using segment tree

Make three arrays namely b, c, d.

b will store p * a[i] , c will store for q and d will store for r.

Make two segment trees (max query) for b and c namely tree1 for b and tree2 for c.

Start iterating array d.

For every di , find max in tree2 first from 0 to i range. Store it as a pair. This pair will store the max value of array c from range 0 to i and the position of that element (pos) in array c. After that, find max value of array b from 0 to pos.

For same di, find max now in tree1 first from 0 to i range. Store it as a pair (say R) again. This pair will store the same as above but now for array b first. Now, find the max value of element in array c from R.second to i.

Since now we are having two values for each di , keep taking max out of it from i = 0 to n.

The final result will be the answer.

For more details, here is my solution — http://codeforces.net/contest/855/submission/30682061

→ Reply
»
7 years ago, # |
  Vote: I like it +18 Vote: I do not like it

Fun linear solution for D: 30688152

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you explain it in detail?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it
      Hint
      Spoiler
      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        you may have interchanged type 1 & 2.

        → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

In Problem C, can anyone provide me an explanation on this part?

Then, we can combine them two nodes at a time to form the dp array for the node curr.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 7   Vote: I like it +20 Vote: I do not like it

    let's say we want to calculate dp[v][j][x] (means the number of ways of getting x number of k type nodes in the subtree rooted at v, where type(v)=j) how to calculate this — let's assume f(v, j, x) has the same definition as dp[v][j][x].

    say we have n children of node v. so essentially what we need to find is the number of ways to distribute x among these n children.

    here we can use a dp. (for convenience I'll call nodes of type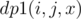 k as special node) Now, to do this computation at node v, we will form another DP dp1. We say as the number of ways to choose a total of x special nodes from subtrees defined by v1,  v2,  ...,  vi i.e. from first 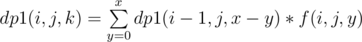i nodes. The recurrence can be defined as , i.e. we are iterating over y assuming that subtree of vi contributes y special nodes and rest x-y special nodes have been contributed by previous i-1 nodes. So, finally dp[v][j][x] = dp1(n, j, x)

    In the editorial solution this dp1 is denoted by a and b array. you wont find i in the editorial's dp1 state, i can be avoided by using two arrays a and b. we store dp1(i, , ) in b array, and after its calculation it is added to a array, so this will become dp1(i - 1, , ) for the next iteration.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But in dp1 you dont memorise which node you are currently at, so values will always mix? I mean, first i childs of node u may mix with first i childs of some other node.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        The graph is a tree. The graph has n-1 edges and is connected ,so every node can have at most 1 parent.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        For every non leaf node v in the tree, we are doing this dp1() calculation locally for that node independent from others. see this part in the editorial's code -

        void dfs(int curr, int par)
{
//something

for(i=0;i<3;i++)
	{
		for(j=0;j<=x;j++)
		{
			a[i][j]=0;
			b[i][j]=0;
		}
	}
	for(i=0;i<3;i++)
		a[i][0]=1;

//calculation of a and b here

for(l=0;l<=x;l++)
	{
		dp[cur][0][l]=(1ll*a[0][l]*(k-1))%mod;
		if(l>=1)
			dp[cur][1][l]=a[1][l-1];
		dp[cur][2][l]=(1ll*a[2][l]*(m-k))%mod;
	}

}

        see at the end we assign the a values to dp state of that node, for next node again a and b arrays will be assigned 0 values at the start in the dfs().

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      So doesn't this solution makes the complexity O(n*x) rather than O(x*x)? Because for each child node, we iterate through the number of special nodes from 0 to x.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      while calculating dp1(i, 0, k) why don't we are considering the values at type 1 and type 2?

      i have used similar approach but failed : http://codeforces.net/contest/855/submission/30802240

      i know i am missing something please help me !

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        here dp1(i, 0, k) states node v is of 0 type. Doesn't make sense. Please read the comment carefully. or maybe I didn't get you?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          " While assigning the value to dp[curr][1][cnt], we take into account only the values of dp[childofcurr][0][cnt - z]. Similarly for dp[curr][2][cnt], we take into account only dp[child of curr][0][cnt - z] and dp[child of curr][2][cnt - z]. "

          I understand this as while calculating the value of type(0) we have to take the values of type(1) , type(0) and type(2) and for type(1) we take only of type(0) below it.

          so, in your comment in the last part it is written that dp(i, j, k) = dp1(n, j, k) doesn't it include the value of type(1) ot type(2) if j = 0!

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain C with more detail ?

I don't get how adding all the dp values of each pair would be the same as taking all combinations among children

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem B , Why the below approach doesn't work? find min , max in array. ans = 0; If(p<0) ans += p * min else ans += p * max Repeat for q and r print ans.

→ Reply
»
7 years ago, # |
  Vote: I like it +7 Vote: I do not like it

Why is the contest getting so much hate?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +85 Vote: I do not like it

    Because problem statements were garbage and problems are not interesting.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

When the editorial of problem E and F will be updated? I am wating for those since yesterday. :(

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hello,

Can somebody explain for problem F (NAGINI) why my solution here receives a TLE for test case 30.

I have tried everything i could to optimise the code.

Thank You.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +43 Vote: I do not like it

F can be solved by special segment tree, which is called Ji driver segment tree in China. You can see this code: http://codeforces.net/contest/855/submission/30680703

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Where can I learn about it? Google search doesn't yield any similar result.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Sorry, I only have Chinese learning materials. Try to understand it by reading the code...My English is very poor, so I can't explain it in English.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Any online material? Then maybe google translate could help!!

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Sorry, this code is not Ji driver segment tree, but you can learn it from: http://www.shuizilong.com/house/archives/hdu-5306-gorgeous-sequence/

          And you can learn Ji driver segment tree from: http://www.doc88.com/p-6744902151779.html

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +3 Vote: I do not like it

            Thanks. :)

            → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +13 Vote: I do not like it

            Isn't this simply the trick to store in each node of the segment tree a flag if all elements/positions have the same value and then in the query and update we update only if the values of the whole segment are equal (else we just continue down)?

            PS: example problem done with the same trick.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
              ← Rev. 3   Vote: I like it +11 Vote: I do not like it

              Looks like yes, in the tutorial in chinese they link this problem http://codeforces.net/contest/444/problem/C also, that can be solved with this trick

              → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              I haven't looked to provided links, but I can already say what you're saying is not true.

              Consider following scenario: Firstly you set value of n on interval [1, n], then you use n/2 queries to set values of 0 in intervals [i, i] for odd i and then you make n queries with value of n-1, n-2, ... on interval [1, n]. All queries from last phase will update values in all even points, so if we use "typical lazy propagation" which you described we will end up having complexity O(n) per query.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                ← Rev. 4   Vote: I like it +3 Vote: I do not like it

                Well, I didn't understand your case, so I will explain the main idea in this problem, first we reduce the problem to:
                We have a array A of size N initially every element is equal to infinity and we can do:
                Update in position: pos k, make A[pos] = k
                Update in range: l r k, for every element i in the interval [l, r] make A[i] = min(A[i], k)
                Query: l r, ask for the sum of every element different of infinity on the interval [l, r]

                So, to solve this with the idea of the segment tree, we gonna keep for every segment what is the biggest element in that segment, how much times the biggest element appears on the segment , the second biggest segment on segment, the sum of the segment and a variable to indicate the lazy propagation

                If we gonna do soma update in pos we just change the value of the biggest element, how many times appear and sum of the node in segment tree that represent this element.

                When we gonna process some update we gonna do the recursive procedure of the segment tree:
                if the current node is out of the interval of update, there is nothing to process in this node
                if the max element in the range of current node is smaller than k, there is nothing to process in this node
                if the range of current node is completely inside of the range of update and the second biggest element is smaller than k, we gonna process this node, the only thing that will change will be the sum of the interval and the biggest element element also we gonna sinalize the lazy propagation
                Else we gonna recurse to the left son and right son, after this we gonna recalculate the value of the nodes where the recursion passed.

                If we gonna query, we just do the normal of the segment tree, taking the sum value of each node

                If I would say the complexity it would be in O(QN) in a trivial analise, but my intuition say that it's faster. My code is 30763830 . Can you say what is the complexity ?

                → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 3   Vote: I like it +15 Vote: I do not like it

            What is this solution's complexity? It was kinda a big fuss in Polish community when Marcin_smu solved it faster than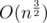 , namely in 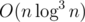using some mergeable leftist tree.

            EDIT: Ok, Google translate told me that it is written that it is n log n. If that's true then it is very impressive

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it +35 Vote: I do not like it

              Well, I'll write a blog about this trick of segment tree later.

              It can change the operation "range max/min" into the trivial operation "range add/minus" in extra time complexity (may be O(1) but I can't prove it yet, I'm still working on it).

              This problem is just a simplest application and segment tree can solve it in .

              BTW, I prefer to call this trick "Segment Tree Beats". I like this name very much :)

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it +26 Vote: I do not like it

                Any news about the blog post? Thanks in advance :)

                → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it +15 Vote: I do not like it

                Any news about the blog post? Thanks in advance :)

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +31 Vote: I do not like it

                  My final exam is finally finished. I'm going to start to work now :)

                  Sorry for the long delay.

                  → Reply
»
7 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Complexity

Yeah, great... And then we are wondering how people managed to squeeze naive bruteforces

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Any special reason to subtract mod instead of just taking the modulus ?, does not seem to save any complexity of computation or coding.

(IN PROBLEM C)

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Can someone give me a readable code for problem D, I find it hard to understand author's code.

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

When will you provide the editorial for the last problem? It's been two weeks.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can Anyone please elaborate more on 855G solution , especially proof of 2nd statement and bit more explanation of 4th statement

→ Reply