В данной задаче нужно было реализовать то, что написано в условии, то есть считать данные и для каждой задачи посчитать количество участников команды, уверенных в ее решении. Если таких участников больше одного, то к ответу прибавить единицу.
231B - Магия, волшебство и чудеса
Для того чтобы быстро и элегантно решить эту задачу, можно рассмотреть, каким будет последнее число массива после i итераций. После первой итерации оно будет равно an - 1–an (при этом количество элементов уменьшится на единицу). После второй –-- an - 2–an - 1 + an. Очевидно, что после n - 1 итерации останется a1–a2 + a3–a4 + ... + ( - 1)n + 1·an. Таким образом, наша задача состоит в том, чтобы расставить в массиве числа от 1 до l так, чтобы сумма чисел стоящих на нечетных позициях минус сумма чисел на четных позициях была равна заданному d. Тогда мы должны на нечетных позициях набрать число, равное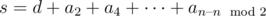 
. При этом минимальное число, которое мы сможем набрать 
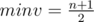, а максимальное –-- 
.
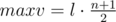Поэтому нужно подобрать a2·k так, чтобы s укладывалось в эти границы. Ограничения позволяли сделать это следующим образом. Расставим сначала на четных позициях единицы. Теперь если s > maxv, то ответ - 1. Иначе будем увеличивать каждое a2·k на единицу до тех пор, пока s < minv. Если, даже расставив на всех четных позициях l, окажется, что s < minv, то ответ также - 1. После того, как мы расставили значения на четных позициях, ставим 1 на всех нечетных местах, и пока сумма этих элементов меньше s увеличиваем каждое из них на допустимую величину.
Для решения этой задачи нужно было заметить, что второе число ответа всегда совпадает с каким-то из чисел исходного массива. Это можно объяснить следующим образом. Предположим, второе число ответа равно aj + d для какого-то j и при этом aj + d ≠ ai ни для какого i. Это значит, что мы увеличили некоторые числа, меньшие aj, до значения aj, а затем эти числа, вместе с некоторыми числами, равными aj, увеличили до значения aj + d. Но если бы мы не увеличивали все эти числа до aj + d, а оставили равными aj, то потратили бы меньше операций увеличения и при этом улучшили бы ответ.
Используя этот факт можно решать задачу следующим образом. Отсортируем исходный массив по неубыванию. Переберем второе число ответа –-- ai и посчитаем, какое мы можем получить максимальное первое число ответа. Для того чтобы максимизировать первое число ответа, нам надо увеличить некоторые меньшие числа до значения ai, при этом используя максимум k операций. Очевидно, что в первую очередь нужно увеличивать те aj, для которых ai–aj минимально. То есть если бы можно было решать задачу за O(n2), то мы бы шли по j от i налево и увеличивали aj до значения ai, пока хватает операций. Однако нужно более быстрое решение. Поэтому нам поможет бинарный поиск по ответу. Мы будем бинарным поиском перебирать количество чисел, которые нужно сделать равными ai. Предположим мы зафиксировали cnt эту величину. Теперь нам нужно за O(1) проверить, можно ли за не более чем k операций сделать cnt чисел равными ai. Для этого подсчитаем следующую величину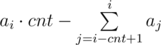 
. Если эта величина не превосходит k, то мы можем это сделать. Для того чтобы быстро вычислять сумму, нужно подсчитать si частичные суммы на префиксе и тогда si - cnt + 1, i = si–si–cnt. Итого мы получаем решение за O(n·logn).
В данной задаче, по сути, нужно было проверить, что из точки p = (x, y, z) виден центр грани параллелепипеда. Рассмотрим случай, когда грань находится в плоскости z = z1. Для того чтобы можно было все вычисления производить в целых числах, умножим все координаты x, y, z, x1, y1, z1 на 2. Возьмем точку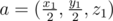 
и вектор нормали к плоскости, содержащей эту грань, который направлен в сторону от внутренности параллелепипеда, то есть 
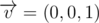. Рассмотрим также вектор 
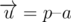. Если неориентированный угол между этими векторами меньше 90 градусов, то из точки p будет видно точку a. Чтобы просто проверить это условие, нужно вычислить скалярное произведение между векторами 
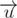и 
, и 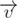если оно строго больше нуля, то угол будет подходящим.
В этой задаче нужно было в вершинном кактусе для некоторых пар вершин найти количество простых путей между ними. Изучив структуру данного вида графов, можно понять, что если сжать каждый цикл вершинного кактуса –-- то получится дерево. Поэтому сожмем циклы в исходном графе и получим это самое дерево. Также для каждой вершины этого дерева пометим, является ли она сжатым циклом (назовем такие вершины 1-вершинами) или отдельной вершиной в исходном графе (такие назовем 0-вершинами).
Теперь, чтобы найти количество путей между вершинами a и b в исходном графе, проделаем следующее. Обозначим за c вершину, которая соответствует вершине a в полученном дереве (это может быть либо отдельная вершина, либо вершина, соответствующая сжатому циклу, в котором лежит a), за d --– вершину, соответствующую b. Подсчитаем величину deg --– количество 1-вершин на пути из c в d в дереве. Тогда несложно понять, что ответ на запрос равен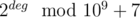 
, так как каждый цикл (1-вершина) увеличивает количество возможных путей вдвое (потому что в цикле из одной вершины в другую можно пройти двумя способами).
Таким образом, для ответа на запрос, нам надо быстро считать количество 1-вершин на пути из одной вершины в другую в дереве. Это можно делать следующим образом. Подвесим полученное дерево за какую-нибудь вершину, которую назовем корнем. Подсчитаем для каждой вершины cntv — количество 1-вершин на пути до корня (включая корень и саму вершину). Допустим, мы хотим найти количество 1-вершин на пути из a в b. Обозначим за c наименьший общий предок вершин a и b. Тогда количество 1-вершин на пути из a в b, равно cnta + cntb–2·cntc, если c является 0-вершиной и cnta + cntb–2·cntc + 1, если c — 1-вершина. Наименьший общий предок можно искать стандартным приемом –-- методом двоичного подъема. Итого мы имеем решение за O(m + k·logn).
Круто вы D решали :)
Я вообще перебирал все грани, проводил прямую к центру. Потом пускал двоичный поиск и смотрел, правда ли что очередная точка лежит в кубе. Если есть такая точка, отличная от центра грани — не добавляем текущее число к ответу.
Очень удивился, увидев решения остальных людей :)
А если рассматривать проекции точек на плоскости, то все сводиться к 6 условиям.
Да, спасибо, я уже в курсе :)
Я делал тоже самое :)
Можно было без бп проверить пересечение прямой и плоскости.
Я проверял не пересечение, а факт "очередная точка, пренадлежащая прямой, принадлежит также и кубу". Хотя по сути в данном случае это одно и то же.
Да, круто и ДА, ЕЛЕГАНТНО)))
Почему бы не дать в Е реберный кактус? :)
А если серьезно — мне непонятно, с какой целью Вы сделали контест с четырьмя халявками и одной реализацией матрешки стандартных алгоритмов.
как быстро и правильно сжать граф в E? если можно, то подробно объясните, так как за контест так и не придумал это! Спасибо.
Пустим ДФС из произвольной вершины. Для каждой вершины храним пометку посещенности, высоту и предка. В случае перехода в непомеченную запускаем ДФС из неё, если нашли уже помеченную = это цикл, его нужно сжать.
У нас есть две соседние вершины из цикла. Если мы будем идти по их предкам, мы обойдем весь цикл и начнем дальше подниматься по дереву. Единственная проблема = два указателя могут не встретиться, так как эти соседние вершины могут находиться на разном расстоянии от первой вершины цикла. Для этого мы и считали высоты: для более глубокой вершины поднимемся по предкам на нужное расстояние, а затем будем двигать указатели по предкам пока они не встретятся.
Фигово объясняю, простой код: http://pastie.org/4928747
до меня кое-что дошло, а алгоритм поиска фундаментального множества циклов здесь можно было использовать?
Ещё один подход: идём дфс-ом, храним метки
inиoutдля каждой вершины, аналогично как при поиске циклов в ориентированном графе. Т.е., когда входим в вершину, ставимin, а когда выходим из неё, ставимout. Если мы встретили вершинуx, у которой помеченin, то мы набрели на цикл, тогда возвращаемx— этот номер будет также номер новой вершины (сжатого цикла). Возвращаемxобратно проходя по циклу до тех пор, пока не заходим обратно в вершинуx, то цикл мы обошли, и возвращаем-1. Так мы будем знать, что родитель не находился в циклеx. А когда проходили по циклу обратно, то присваивали вершинам в цикле значениеx, т.е., номер сжатой вершины. Если же мы проходим не по циклу, то присваиваем номер такой же, как был для вершины в данный момент. В общем, код.Зачем нужны какие-то высоты? Запустим dfs, по пути отмечая посещенные вершины (vis[x] = true) и вершины, принадлежащие циклам (id[x] != -1).
Как только мы пытаемся пойти в посещенную, но не помеченную вершину, это значит, что мы нашли ранее необработанный цикл — в этом случае раскручиваем путь по предкам и проставляем id.
Это все. В конце надо одиночным вершинам тоже присвоить id, и в id[x] будет храниться номер вершины в сжатом графе.
Вот код
Видимо если вы предполагали такое решение в D, нужно было как-то повернуть фигуру, чтоб грани не были параллельны плоскостям.
Обидно, подумал что вершины не могут повторяться в простых путях и пришлось отдельно обрабатывать случаи, когда есть цикл и из одной вершины этого цикла свисает две веточки(
Моё решение B чуть проще для понимания: Как и в офф разборе, понимаем что знаки чередуются. Расставим на нечётных позициях L а на чётных 1, тогда получится расстановка с максимально возможной суммой. Теперь просто пробегаемся по массиву, на i-ом шаге если текущая сумма массива больше нужной, то пытаемся её уменьшить: для чётных i уменьшить значение i-го элемента, для нечётных увеличить. Таким образом мы плавно спускаемся к нужной отметке. Вот код: http://codeforces.net/contest/231/submission/2313643
По-моему в D есть гораздо проще объяснение, для того чтобы увидеть одну из граней, надо находиться в соответствующем полупространстве, т.е., например, x > x1 или x < 0 и все. вот 2315503
Спасибо, Кэп.
Полупространство там, а не полуплоскость
Извиняюсь, описался, все равно заминусовали.
I solved Problem B by dfs :
Lets maintain two arrays ,d[] the array of differences and a[] the array of numbers . Initially d[0]=d . Now we know that a[0] lies in the range of [1...L] and a[0]-d[1]=d[0] => d[1]=a[0]-d[0].So we need to iterate over all possible values of a[0] i.e [1..L] and check if it is going good .Similarly we check for d[1] and keep digging deeper until we reach the base case ( index=n-1) . My code implementing the above idea code ..As you see the code exceeded time on pretest 10 (call it lucky or unlucky).
So other thing to observe is what is the maximum ans minimum values that the difference array can take. With this we can prune the tree into avoid going to some branches which are unncessary . Lets take the trivial values of max and min for the last location . i.e . d[n-1] as max[n-1]=L ans min[n-1]=1. Now max[n-2]=L-min[n-1] and min[n-2]=1-max[n-1] .So like this , we make up these two arrays . And everytime we are calling the dfs function we check if the d value is in the range of max and min .Code
А, ну понятно, откуда у D 2000. Но все же 6 if'ов вроде бы даже очевиднее.
It will be great if you can post the implementation code for these solutions as well.
If you really need them, you could see other participants' solutions in the standing page.
this is the solution of A.team
include
include
using namespace std; int main() { int n,i,j,c; vector v; cin>>n; int arr[n][3]; for(i = 0;i<n;i++){ for(j = 0;j<3;j++){ cin>>arr[i][j]; } } for(i = 0;i<n;i++){ c = 0; for(j = 0;j<3;j++){ if(arr[i][j] == 1){ c = c+1; } } if(c >=2){ v.push_back(1); } } int ans = 0; for(i = 0;i<v.size();i++){ ans = v[i] + ans; } cout<<ans; return 0; }
А вот самое простое и короткое решение B: Пусть di — разность между элементами ai и ai + 1 восстановленного массива.
Присваиваем минимальное подходящее значение ai = 1 при di < 0 и ai = min(di + 1, n) при di ≥ 0, тогда по условию задачи ai + 1 - ai + 2 = ai - di, и переходим к следующей итерации.
d0 нам задано. Очевидно что первые n - 1 чисел лежат в нужных пределах, таким образом остается проверить последнее число и вывести ответ.
Why there is no English tutorial, I can't understand Russian...
http://codeforces.net/blog/entry/5486
Change the url from http://codeforces.net/blog/entry/5486 to http://codeforces.net/blog/entry/5486
Or simply press the British flag on the top right corner of the page
Просматривал решения тех, кто успешно сдал B, и наткнулся на интересное решение за O(n), но не понял почему это работает :( Кто поймет, объясните пожалуйста :) Вот само решение : 2317805
А у автора спросить не судьба?
Это решение эквивалентно авторскому с той разницей, что, согласно авторскому решению, нужно ставить минимально возможные числа, дающие в итоге нужное d, а Aman поступает наоборот: ставит максимально возможные числа.
P.S. Я очень удивлен тем, что серебряный призер IOI пишет такой мутный говнокод.
Почему "мутный говнокод"? Его решение не занимает много строк, да и тем более верно. Но если вы про то как он пишет всё сжато, то как я думаю это его право.
ОК, откажусь от слова "мутный" (предположу, что он это решение придумал уверенно и для него самого код кристально понятен даже через год после написания).
Почему "говнокод"? Ну, потому, что в нормальном коде хотя бы расставляются отступы.
"Ну, в фаре когда на скобку встаешь, сразу же вторая подсвечивается и все становится понятно. Зато мой код самый маленький по количеству символов на кодфорсес!" (с) Аман Сариев, серебряный призер IOI
Warning — I am a complete newb at online coding competitions, so if dealing with people like me causes you lots of frustration, please just ignore my comment and pass on!
I competed in this competition (only submitted on 231A Team) I was wondering if someone might hop into a 'talk' me and help me understand why my solution was incorrect (my code is so ugly I dont want to post it here)? I had it working fine my version of Visual Studio, but when I submitted it didn't pass the first test...think it's probably something to do with how I read the stdin...
Any help gratefully received — thanks. ahab
There are spaces between the numbers in the input data. Your method of inputting data is weird. Why use
strings andstringstreams if you can read numbers directly fromcin?Thanks for the reply — you're right. It was weird to use
string(The perils of being newb coder!) and I just realised my error this morning with the spaces between the letters when I started stepping through someone else's succussful submission. Thank you for taking the time to look.Out of interest, when you are coding and debugging your potential submissions, how do you replicate the standard input? Do you set up the examples given in the problem in a file and point
cinto that, or do you type them in by hand as required by your code as you execute a trial run?One popular way to do it is to store test input in a file and then insert
#ifndef ONLINE_JUDGE freopen("input.txt", "r", stdin); #endifat the beginning of
main().Then you would use
cinas usual. TheONLINE_JUDGEmacro is defined on Codeforces, so this code will redirectcinif you compile it on your computer and will still read from standard input if compiled on Codeforces. You can also do the same for output withfreopen("output.txt", "w", stdout);.Then there is a problem of inputting multiple test cases. Many people deal with it like this: they store all tests in one file, and in the main program write
while (cin >> first_variable_of_input) { // Read remaining data for this test case // Process data and print the answer }While there is something yet to be read from file, this loop will begin anew, allowing to process many tests at once. But be careful to re-initialize all global variables each time. I won't say this is the best solution, but it is simple and quick enough to write.
Could somebody help me with the sample for problem E: points 3-5, isn't the number of simple paths equal to 3? 3-2-1-4-3-5, 3-4-1-2-3-5, 3-5? what am i missing?
For E — Cactus, can someone explain the algorithm needed to "squeeze" the cycles?
Could anyone explain this part in the editorial for 231C please?
" Suppose we fix cnt this value. Now we have to check if we can do cnt numbers equal to ai by not greater than k operations. For doing this, let’s calculate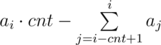
. If this value not greater than k, we can do it. For calculating sum quickly, we can save prefix sums and than si - cnt + 1, i = si–si–cnt."
P231C is possible in O(n) using two pointers. First Input n,k,array (a). Sort array a.
You need mocc and mnum.
I didn't understand the part:
please explain, thank you.
we are restoring back the total difference, tdiff.
While your
..., the time complexity still same as the official solution:(
sortis inSolution to div2 C using 2 pointers . Works in O(n) apart from sorting
code
Can you explain how you used two pointers in this?I solved using the author's solution
sort() == O(nlogn)
apart from sorting
A much easier to solution D is to simply check for each dimension whether the observer's position for that dimension is less than 0, more than x1/y1/z1, or in between.
For example, if observer's x is less than 0, the a5 side will be visible no matter the observer's y and z, if the observer's x is more than x1 (where the cube ends) then the a6 side will be visible no matter the observer's y and z. Do the same for the other 2 dimensions and you get the sum. No angle calculations necessary.
Program: https://codeforces.net/problemset/submission/231/53533694
Pls, tell me whether my logic for E is correct or not.
Since it is a cactus, we can detect all cycles within o(n), I will mark different cycles with different colors(such that the nodes within the same cycle have the same colors), such coloring is possible cuz one vertex is a part of at most one cycle.
To respond to the query, I would check 3 cases. I) Suppose their color is the same, then there are 2 possibilities to reach from end x_i to y_i.
ii) Suppose their color is different color then there would be always 4 possible ways.
iii) if some node is not colored, it means it is not part of any cycle, thus there would be only one path to reach that node (if both the nodes are not colored), 2(if one node is colored and the other is not(